- •Введение
- •1.Основы квантовой теории
- •1.1. Электроны
- •1.2. Излучение абсолютно черного тела
- •1.3. Фотоэлектрический эффект
- •1.4. Корпускулярно-волновой дуализм
- •1.5. Основы квантовой теории
- •1.6. Волновые функции
- •1.7. Принцип неопределенности
- •1.8. Дополнительные сведения по квантовой механике
- •1.8.1. Волновая функция
- •1.8.2. Соотношение неопределенностей
- •1.8.3. Уравнение Шредингера
- •1.8.4. Частица в одномерной потенциальной яме. Уровни энергии
- •1.8.5. Отражение и прохождение через потенциальный барьер
- •1.9. Основные выводы
- •1.10. Контрольные вопросы
- •1.11. Задачи
- •2. Теория поля
- •2.1 Скалярные и векторные поля
- •2.2 Гравитационное поле
- •2.3 Гравитационный потенциал
- •2.4 Электрическое поле
- •2.5 Поле ядерных сил
- •2.6 Энергия поля
- •2.7. Дифференциальные операции в скалярных и векторных полях
- •2.7.1. Скалярное поле
- •2.7.2. Векторное поле
- •2.7.3.Производная по направлению
- •2.7.4. Градиент скалярного поля.
- •2.7.5. Потенциальное поле
- •2.7.6. Дивергенция
- •2.7.7. Ротор
- •2.7.8. Примеры решения задач
- •2.8. Интегральные характеристики векторных полей
- •2.8.1. Поток векторного поля
- •2.8.2. Формула Остроградского – Гаусса в векторной форме.
- •2.8.3. Соленоидальные поля и их свойства
- •2.8.4. Инвариантное определение дивергенции
- •2.8.5.Циркуляция векторного поля
- •2.8.6.Формула Стокса в векторной форме
- •2.8.7.Свойства потенциального поля
- •2.8.8. Инвариантное определение ротора
- •2.8.9. Примеры решения задач.
- •2.9. Оператор Гамильтона
- •2.9.1. Определение оператора Гамильтона
- •2.9.2.Правила вычислений с оператором
- •2.9.3. Примеры решения задач
- •2.10. Контрольные вопросы.
- •2.11. Задачи.
- •3 Теория относительности
- •3.1. Основы теории относительности
- •3.2 Преобразования Лоренца
- •3.3 Изменение массы в зависимости от скорости
- •3.4. Масса и энергия
- •3.5 Общая теория относительности
- •3.6. Основные выводы
- •3.7.Контрольные вопросы
- •3.8. Задачи
- •Заключение
- •Приложение
- •Библиографический список
3.3 Изменение массы в зависимости от скорости
Первый постулат теории относительности гласит, что все физические законы одинаковы во всех инерциальных системах отсчета. К числу таких законов относится закон сохранения импульса, что приводит к тому, что масса тела зависит от скорости его движения.
Рассмотрим двух наблюдателей в системах
отсчета
![]() и
и![]() ,
движущихся относительно друг друга со
скоростью
,
движущихся относительно друг друга со
скоростью![]() .
В каждой из систем отсчета имеется
неподвижное тело массой
.
В каждой из систем отсчета имеется
неподвижное тело массой![]() .
Тела расположены так, что когда системы
отсчета пролетают друг мимо друга,
происходит скользящее соударение тел.
Иными словами, каждое из тел при ударе
приобретает небольшую скорость под
прямым углом к направлению относительного
движения систем
.
Тела расположены так, что когда системы
отсчета пролетают друг мимо друга,
происходит скользящее соударение тел.
Иными словами, каждое из тел при ударе
приобретает небольшую скорость под
прямым углом к направлению относительного
движения систем![]() и
и![]() (т.е. в поперечном направлении). Тело в
системе
(т.е. в поперечном направлении). Тело в
системе![]() обладает поперечными скоростью
обладает поперечными скоростью![]() и импульсом
и импульсом![]() ,
измеренными наблюдателем, находящимся
в этой системе. Аналогичными величинами
обладает тело в системе
,
измеренными наблюдателем, находящимся
в этой системе. Аналогичными величинами
обладает тело в системе![]() .
Если наблюдатели в этих системах
обменяются данными о скорости тела в
«своей» системе отсчета, то полученные
ими результаты в точности совпадут.
Однако если наблюдатель
.
Если наблюдатели в этих системах
обменяются данными о скорости тела в
«своей» системе отсчета, то полученные
ими результаты в точности совпадут.
Однако если наблюдатель![]() попробует наблюдать за правильностью
измерений в системе
попробует наблюдать за правильностью
измерений в системе![]() ,
то он заметит, что часы наблюдателя
,
то он заметит, что часы наблюдателя![]() идут слишком медленно. К такому же выводу
придет наблюдатель
идут слишком медленно. К такому же выводу
придет наблюдатель![]() ,
контролируя измерения наблюдателя
,
контролируя измерения наблюдателя![]() .
В результате по расчетам наблюдателя
в
.
В результате по расчетам наблюдателя
в![]() скорость тела в системе
скорость тела в системе![]() оказывается меньше, чем та скорость,
которую измерил наблюдатель
оказывается меньше, чем та скорость,
которую измерил наблюдатель![]() .
Скорость будет меньшей в отношении
.
Скорость будет меньшей в отношении![]() .
Но если скорость меньше, а закон сохранения
импульса считается по-прежнему
справедливым, то получается, что масса
тела в системе
.
Но если скорость меньше, а закон сохранения
импульса считается по-прежнему
справедливым, то получается, что масса
тела в системе![]() должна быть, по мнению наблюдателя в
должна быть, по мнению наблюдателя в![]() ,
больше чем масса в системе
,
больше чем масса в системе![]() ,
причем в отношении
,
причем в отношении![]() .
.
В результате оба наблюдателя придут к мнению, что масса движущегося тела больше массы такого же покоящегося тела. Возрастание массы с увеличением скорости (точно так же, как и сокращение размеров и замедление течения времени) оказывается симметричным для наблюдателей в обеих системах отсчета, находящихся в относительном движении.
Масса тела, измеренная в той системе
отсчета, относительно которой тело
покоится, называется массой покоя,
илисобственной массой, и
обозначается![]() .
Тогда масса
.
Тогда масса![]() ,
измеренная наблюдателем, движущимся
относительно тела со скоростью
,
измеренная наблюдателем, движущимся
относительно тела со скоростью![]() ,
равна
,
равна
![]() . (3.23)
. (3.23)
Из этого соотношения следует заключить,
что скорость материального тела не
может достичь скорости света или
превысить ее, поскольку при
![]() множитель
множитель![]() обращается в нуль и
обращается в нуль и![]() становится бесконечно большой. Разумеется,
бесконечная масса не имеет физического
смысла, и отсюда вытекает, что все
материальные тела могут двигаться со
скоростями, меньшими скорости света.
Вместе с тем, согласно правилу сложения
скоростей (3.3), такой вывод будет справедлив
в любой системе отсчета.
становится бесконечно большой. Разумеется,
бесконечная масса не имеет физического
смысла, и отсюда вытекает, что все
материальные тела могут двигаться со
скоростями, меньшими скорости света.
Вместе с тем, согласно правилу сложения
скоростей (3.3), такой вывод будет справедлив
в любой системе отсчета.
Различие между массами
![]() и
и![]() чрезвычайно мало до тех пор, пока скорость
чрезвычайно мало до тех пор, пока скорость![]() не начинает составлять заметную долю
скорости света. По этой причине
релятивистское возрастание массы с
увеличением скорости нельзя обнаружить
в мире повседневных скоростей. Возрастание
массы удается заметить только когда мы
имеем дело с элементарными частицами,
разгоняемыми в ускорителях до высоких
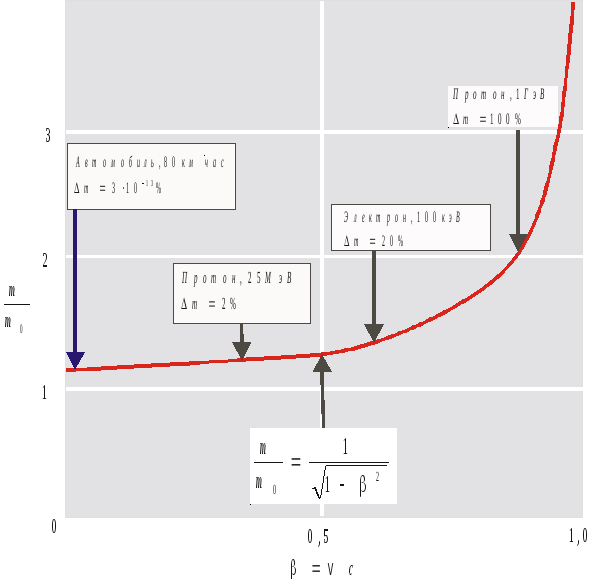
скоростей. На рис. 3.9 дано графическое
изображение формулы (3.23).
не начинает составлять заметную долю
скорости света. По этой причине
релятивистское возрастание массы с
увеличением скорости нельзя обнаружить
в мире повседневных скоростей. Возрастание
массы удается заметить только когда мы
имеем дело с элементарными частицами,
разгоняемыми в ускорителях до высоких
скоростей. На рис. 3.9 дано графическое
изображение формулы (3.23).
|
|
|
Рис.3.9. Релятивистское возрастание массы с увеличением ее скорости |
Видно, что масса протона с энергией 1 Гэв вдвое превышает массу покоящегося протона, тогда как увеличение массы совершенно незначительно автомобиля.
Возрастание массы тела, движущегося со скоростью, малой по сравнению со скоростью света, равно
![]() . (3.24)
. (3.24)