2.8.4. Инвариантное определение дивергенции

Пусть в области ,ограниченной поверхностью, определено векторное поле. Запишем формулу (2.50) для векторного поляв области.Применяя к левой части этой области теорему о среднем, получим

(2.54 а)

или

(2.54 б)

где -объем области , а -некоторая точка области.

Зафиксируем точку и будем стягивать областьк точкетак, чтобыоставалась внутренней точкой области.Тогда,абудет стремиться к. В силу непрерывностизначениебудет стремиться к. Таким образом, получаем

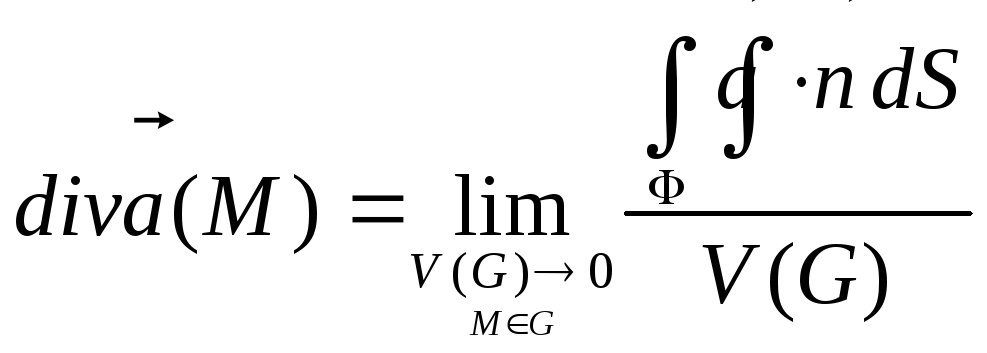. (2.55)

В правую часть формулы (2.5) входят величины, инвариантные относительно выбора системы координат (поток векторного поля через поверхность и объем области). Поэтому формула (2.5) дает инвариантное определение дивергенции. Итак, дивергенция векторного поля зависит только от самого поля и не зависит от выбора системы координат.

2.8.5.Циркуляция векторного поля

Рассмотрим векторное поле , определенное в пространственной области ,и некоторую кусочно-гладкую кривую, на которой указано направление обхода (выбор направления называют также ориентацией кривой).

Пусть - единичный касательный вектор к кривойв точке, направленный в сторону обхода кривой. Криволинейный интеграл

(2.56)

называется циркуляцией векторного поля вдоль кривойв заданном направлении.

Если взять другое направление обхода кривой (изменить ориентацию), то вектор изменит направление на противоположное, поэтому скалярное произведение ,а значит, и циркуляция (криволинейный интеграл (2.6)) изменит знак.

Если - силовое векторное поле, т.е.- вектор силы, то циркуляцияпредставляет собой работу силового векторного поля вдоль кривой в заданном направлении.

Если в прямоугольной системе координат , а, то выражение (2.56) для циркуляции поляможно записать в следующем виде:

(2.57)

Каждое слагаемое в правой части (2.7) зависит от выбора системы координат, однако их сумма, т.е. циркуляция , очевидно, не зависит от выбора системы координат.

Если ввести вектор , то циркуляцию можно записать в виде.

2.8.6.Формула Стокса в векторной форме

Пусть в области определено векторное поле;-замкнутый контур, лежащий в области ; -произвольная поверхность, границей которой является контур ;(говорят, поверхностьнатянута на контур );-единичный вектор нормали на выбранной стороне поверхности.

Пусть для векторного поля ,т.е. для функцийи поверхностивыполнены условия: функции -непрерывны и имеют непрерывные частные производные первого порядка. Тогда справедлива формула Стокса

, (2.58)

где ориентация контура согласована с ориентацией поверхности. Левая часть формулы Стокса есть циркуляция векторного полявдоль контура ,а правая часть представляет собой поток через поверхностьвекторного поля с коэффициентами, т.е. потокчерез поверхность.

Поэтому формулу Стокса можно записать в векторной форме:

. (2.59)

Таким образом, циркуляция векторного поля вдоль замкнутого контура равна потоку ротора векторного полячерез поверхность, натянутую на этот контур.

Чтобы циркуляция была отлична от нуля для малого контура, окружающего некоторую выбранную точку поверхности, поле должно поворачиваться (иметь завихрение) вблизи этой точки. Из формулы Стокса следует, что тогда ивблизи этой точки будет отличен от нуля. Таким образом,характеризует завихрение поля в точке. Отсюда и происходит название "вихрь" или "ротор".