2.3 Гравитационный потенциал

Гравитационная потенциальная энергия пробной массы , находящейся в покое на расстоянииот источника поля массой, определяется как

. (2.8)

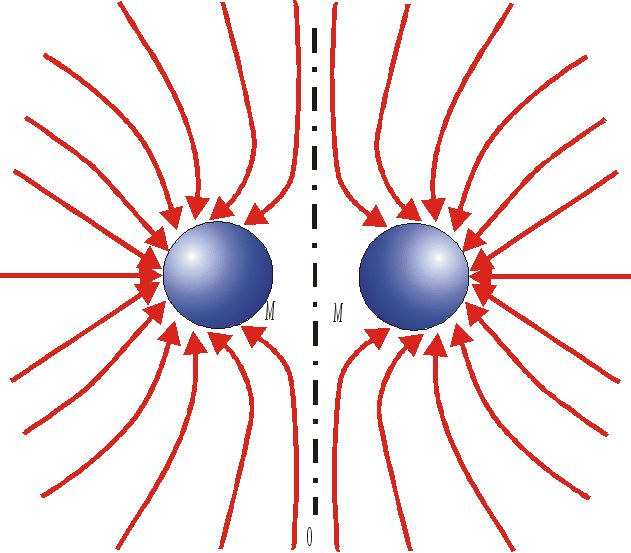
Рис.2.7. Силовые линии поля двух одинаковых близко расположенных тел массой

Если разделить гравитационную потенциальную энергию на , то получится величина, характеризующая поле источника массойи не зависящая от величины пробной массы. Эта новая величина называетсягравитационным потенциалом

. (2.9)

Гравитационный потенциал есть потенциальная энергия, приходящаяся на единицу массы.

Гравитационный потенциал есть величина скалярная, и для него справедлив принцип суперпозиции:

. (2.10)

Ясно, что величина имеет определенное значение в каждой точке пространства и удовлетворяет всем требованиям, предъявляемым к понятию поля. Поэтому можно сказать, чтопредставляетскалярное поле гравитационного потенциала, тогда какпредставляетвекторное поле гравитационной силы.

Согласно соотношению (2.10), гравитационный потенциал поля однородного тела сферической формы зависит только от радиального расстояния до этого тела. Этот потенциал одинаков для любой точки сферы, центром которой является источник поля. Поверхность такой сферы называется эквипотенциальной. Таким образом, для источника в виде однородной сферической массы эквипотенциальные поверхности представляют собой ряд сфер (рис.2.8)

Ранее мы говорили, что силовые линии сферического источника есть прямые линии, направленные от него по радиусам. Следовательно, эти силовые линии пересекаются с эквипотенциальными поверхностями под прямым углом, причем это утверждение имеет совершенно общий характер, т.е. для любых источников поля или группы таких источников силовые линии и эквипотенциальные поверхности всегда взаимно перпендикулярны.

Рис.2.8. Эквипотенциальные поверхности и силовые линии сферического источника

Это утверждение можно доказать следующим образом. Известно, что для перемещения тела с постоянной скоростью перпендикулярно направлению действующей на него силы не требует совершения работы в отсутствии сил трения. Кроме того, направление, перпендикулярное силе, является единственным, для которого это справедливо. Если работа не совершается ни над телом, ни самим телом, значит, не изменяется и потенциальная энергия тела. Следовательно, при движении тела с постоянной скоростью вдоль эквипотенциальной поверхности (из какой-либо точки в точкуна рис. 2.8) не требуется совершения работы, поскольку при таком движении не происходит изменения потенциальной энергии. Но если при движении по эквипотенциальной поверхности не совершается работа, значит, эта поверхность везде должна быть перпендикулярна силовым линиям.

Какой вид имеют эквипотенциальные поверхности двух одинаковых масс, находящихся на некотором расстоянии друг от друга? Гравитационный потенциал двух масс равен

, (2.11)

где - потенциал в точке, находящейся на расстоянияхисоответственно от первой и второй масс (рис. 2.9).

Рис. 2.9. Эквипотенциальные поверхности поля двух одинаковых сферических масс

Одна из эквипотенциальных поверхностей определяется всевозможными комбинациями значений и, при которыхимеет одинаковое значение. Различные комбинации расстояний дадут другие поверхности с иными, но тоже постоянными по поверхности значениями. Несколько таких поверхностей в разрезе показано на рис.2.9 в трехмерном пространстве эти поверхности получаются при вращении разреза вокруг прямой, соединяющей обе массы.