1.8.4. Частица в одномерной потенциальной яме. Уровни энергии

_{Рассмотрим движение частицы в потенциальном поле, определенном условиями:}

_(1.53)

_{Такое потенциальное поле называют бесконечно глубокой потенциальной ямой. На границе ямы на частицу действуют сколь угодно большие силы, которые не позволяют ей выйти наружу, так что частица заключена в некоторой области пространства. Приближенно можно считать, что в таких условиях находится электрон в металле, движущийся вдоль оси х.}

_{Решение уравнения Шредингера следует искать в двух областях: вне потенциальной ямы и внутри ее. Поскольку частица не может находиться вне потенциальной ямы, ее волновая функция равна 0 вне промежутка . Из условия непрерывности следует, что она равняется нулю также и в точках и , то есть:}

_{. (1.54)}

В области уравнение Шредингера (1.10) для стационарных состояний имеет вид:

. (1.55)

Решение этого уравнения ищется при граничных условиях (1.54). Общее решение уравнения (1.55) имеет вид

, (1.56)

где

. (1.57)

Используя граничные условия (1.54), из соотношения приследует. Из условияприполучим

. (1.58)

Так как , иначебудет тождественно равна нулю, то следует, что:

. (1.59)

Откуда

, (1.60)

где n=1,2,…n,…–любое целое число больше нуля. В дальнейшем его будем называть главным квантовым числом. При n=0 волновая функция тождественно равна нулю, что соответствует отсутствию частицы в пространстве.

Из условий (4.4) и (4.7) найдем возможные значения энергии

. (1.61)

Из формулы (1.61) следует, что уравнение Шредингера (1.55) имеет решение, удовлетворяющее граничным условиям (1.54) только при дискретных значениях энергии. Таким образом, энергия частицы в потенциальной яме оказывается квантованной. Состояние частицы с наименьшей возможной энергией будет далее называться основным или нормальным, все остальные состояния – возбужденные. Энергия основного состояния получается из формулы (1.61) при n=1.

. (1.62)

Найдем расстояние между соседними уровнями энергии

. (1.63)

Расстояния между уровнями энергии уменьшаются с увеличением массы частицы. Относительное расстояние между уровнями стремится к нулю с ростомn, то есть дискретность квантовых уровней перестает проявляться при больших квантовых числах, энергетический спектр становится практически непрерывным.

1.8.5. Отражение и прохождение через потенциальный барьер

_{Рассмотрим движение микрочастицы через границу двух областей с разными потенциальными энергиями. В простейшем случае одномерного движения вдоль оси x с бесконечно протяженным прямоугольным потенциалом (рис. 1.18)}

_{Рис. 1.18}

_{, (1.64)}

_{где .}

В классической механике любая частица, двигающаяся слева направо вдоль оси x c энергией, меньшей высоты барьера , полностью отражается от потенциальной стенки. Областьявляется для нее недоступной, так как в этой области полная энергия частицы была бы меньше потенциальной. Это означало бы, что кинетическая энергия должна была бы быть отрицательной, что невозможно. Если же полная энергияE больше , то по законам классической механики частица беспрепятственно проходит над барьером, двигаясь в областис меньшей кинетической энергией, равной.

Рассмотрим движение микрочастицы в тех же условиях по законам квантовой механики. Для этого воспользуемся уравнением Шредингера для стационарных состояний частицы (1.51) в поле бесконечно протяженного барьера (1.64).

, (1.65)

где U(x) – потенциальная энергия, определяемая формулой (1.64), график которой предоставлен на рис. 1.18

Решение уравнения (1.65) будем искать в двух различных областях: при и при. Запишем уравнение Шредингера для каждой из указанных областей:

_, (1.66)

Здесь обозначено:

(1.67)

Решения этих двух уравнений запишутся в виде:

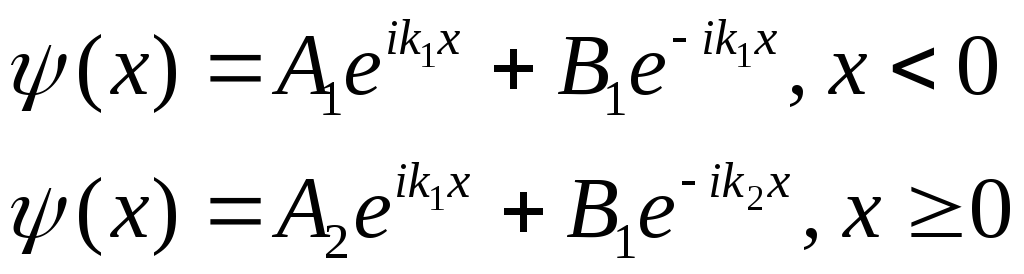_{. (1.68)}

_{В этих формулах слагаемые вида представляют плоскую волну, распространяющуюся в положительном направлении оси x, а плоскую волну, распространяющуюся в обратном направлении. Амплитуды являются постоянными интегрирования. Поскольку амплитуда определяет интенсивность потока частиц, падающих на барьер, то для простоты выберем .}

_{Для определения остальных постоянных воспользуемся условием непрерывности волновой функции и ее производной на границе раздела областей в точке .}

_{Получим}

. (1.69)

. (1.70)

_{Кроме того, следует положить , так как эта величина характеризует амплитуду отраженной волны, распространяющейся в области . Для потока частиц, распространяющихся в положительном направлении оси x, в области 2 отраженная волна отсутствует.}

_{При из соотношений (1.69) и (1.70), учитывая (1.68), получим}

, (1.71)

откуда находим:

. (1.72)

Из выражения (1.72) видим, что амплитуда отраженной волны отлична от нуля, хотя_{. Это обстоятельство обусловлено волновыми свойствами частиц. Волна частично отражается, частично проходит в область 2. Интенсивность отраженной и прошедшей волны характеризует соответственно коэффициент отражения R и коэффициент прохождения D. Получим:}

. (1.73)

При этом выполняется соотношение

, (1.74)

выражающее закон сохранения потока частиц.

Рассмотрим случай, когда . При этом из формулы (1.66) следует, что. Это означает, что-чисто мнимая величина, которую удобно записать в виде, где

. (1.75)

Из формулы (1.72) видно, что амплитуда отраженной и прошедшей волны – комплексные величины

. (1.76)

Коэффициент отражения будет равен

. (1.77)

Отраженная волна запишется в виде

. (1.78)

Так как модуль амплитуды равен единице, то отражение приводит только к сдвигу фазы волны на величину , определяемую по формуле

. (1.79)

Из формулы (1.67) следует, что отражение является полным , но в то же время волновая функция в области 2 отлична от нуля и имеет вид

,. (1.80)

Плотность вероятности того, что частица находится в области , будет равна

. (1.81)

Таким образом, поведение квантовых частиц существенно отличается от классических. Для частицы, двигающейся по законам классической механики, область приявляется недоступной. Частица же, движущаяся по законам квантовой механики, с известной вероятностью может проникнуть в эту область. Проникновение частицы в область запрещенных энергий представляет специфический квантовый эффект, получивший название туннельного эффекта. Эффективная глубина проникновения частицы в области 2 имеет порядок величины. Приплотность вероятности (1.81) экспоненциально мала.