ГОУВПО «Воронежский государственный технический университет» Факультет энергетики и систем управления Кафедра высшей математики и физико-математического моделирования

Курсовая работа

по дисциплине дискретная математика на тему:

«Разработка алгоритма преобразования латинского прямоугольника в латинский квадрат»

Выполнил: студент гр. АТР-131 Романцев Анатолий

Принял: доц. Купцов В. С.

Воронеж 2013 г.

Содержание

Условие задачи…………………………………………………………………………….3

Теоретическое введение…………………………………………………………………..4

Решение……………………………………………………………………………………8

Заключение……………………………………………………………………………….??

Список литературы………………………………………………………………………??

Условие задачи

Цифры 1, 2, 3, …, 9 размещены в латинском прямоугольнике с 8 строками и 9 столбцами. Можно ли и сколькими способами, если можно, добавить одну строку, чтобы получить латинский квадрат?

Теоретическое введение латинский квадрат

Латинский квадрат n-го порядка — таблица L=(l_ij) размеров n × n, заполненная n элементами упорядоченного множества M таким образом, что в каждой строке и в каждом столбце таблицы каждый элемент из M встречается в точности один раз. Пример латинского квадрата 3-го порядка:

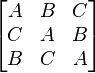
В настоящее время в качестве множества M обычно берется множество натуральных чисел {1,2,…,n} или множество {0,1,…,n-1}, однако Леонард Эйлер использовал буквы латинского алфавита, откуда латинские квадраты и получили своё название.^[1]

Латинские квадраты существуют для любого n, достаточно взять таблицу Кэли аддитивной группы кольца :l_ij= (i+j-1) mod n

Число латинских квадратов

Точная формула для числа L(n) латинских квадратов n-го порядка неизвестна. Наилучшие оценки для L(n) дает формула

^[8]

Каждому латинскому квадрату можно поставить в соответствие нормализованный (или редуцированный) латинский квадрат, у которого первая строка и первый столбец заполнены в соответствии с порядком, заданном на множестве M. Пример нормализованного латинского квадрата:

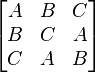
Число R(n) нормализованных латинских квадратов n-го порядка в n!(n-1)! раз меньше, чем L(n).

Точные значения величины L(n) известны для n от 1 до 11:^[9]

Число латинских квадратов
n	R(n)	L(n)	Автор и год
1	1	1
2	1	2
3	1	12
4	4	576
5	56	161280	Euler (1782)
6	9408	812851200	Frolov (1890)
7	16942080	61479419904000	Sade (1948)
8	535281401856	108776032459082956800	Wells (1967)
9	377597570964258816	5524751496156892842531225600	Bammel и Rothstein (1975)
10	7580721483160132811489280	9982437658213039871725064756920320000	McKay и Rogoyski (1995)
11	5363937773277371298119673540771840	776966836171770144107444346734230682311065600000	McKay и Wanless (2005)

Ортогональные латинские квадраты

Два латинских квадрата L=(l_ij) и K=(k_ij) n-го порядка называются ортогональными, если все упорядоченные пары (l_ij,k_ij) различны. Пример двух ортогональных латинских квадратов и соответствующие им упорядоченные пары:

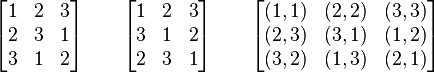
Эйлер называл такие квадраты "полными". В его честь в научной литературе их раньше называли "эйлеровыми" или "греко-латинскими" (так как Эйлер использовал буквы греческого алфавита для квадрата, ортогонального латинскому).

Ортогональные латинские квадраты существуют для любого n, не равного 2 и 6.

Латинский квадрат L n-го порядка имеет ортогональный ему квадрат тогда и только тогда, когда в L существует n непересекающихся трансверсалей.

Особый интерес в связи с многочисленными приложениями вызывают множества из нескольких попарно ортогональных латинских квадратов n-го порядка. Максимально возможная мощность N(n) такого множества равна n-1, в этом случае множество называется полным.

При n, стремящемуся к ∞, величина N(n) тоже стремится к ∞.

Для n, являющегося степенью простого числа, всегда существует полное множество попарно ортогональных латинских квадратов, его можно взаимооднозначно сопоставить с конечной проективной плоскостью порядка n. Для его построения применяется метод Боуза, использующий для заполнения квадратов значения многочленов вида f_a(x,y)=ax+y при ненулевом a над полем .^[11] Пример построения полного множества попарно ортогональных латинских квадратов 4-ого порядка (d – корень примитивного многочлена x²+x+1 над ):

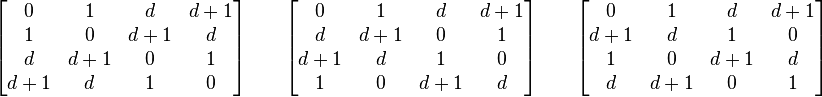
Если n ≡ 1 (mod 4) или n ≡ 2 (mod 4) и свободная от квадрата часть числа n содержит хотя бы один простой множитель p ≡ 3 (mod 4), то для таких n полного множества попарно ортогональных латинских квадратов не существует.

Известные нижние оценки числа N(n) при n < 33 приведены в следующей таблице (выделены оценки, которые могут быть улучшены):

Нижние оценки числа N(n)
n	1	2	3	4	5	6	7	8	9	10	11	12	13	14	15	16	17	18	19	20	21	22	23	24	25	26	27	28	29	30	31	32
N(n)≥			2	3	4		6	7	8	2	10	5	12	3	4	15	16	3	18	4	5	3	22	6	24	4	26	5	28	4	30	31

Построение ортогональных квадратов – сложная комбинаторная задача. Для её решения применяются как алгебраические конструкции, так и комбинаторные (трансверсали, ортогональные массивы, дизайны, блок-схемы, тройки Штейнера и др.) Существует несколько подходов к решению этой задачи, их можно разделить на две группы. К первой группе относятся методы, основанные на выборе базового латинского квадрата, к которому отыскиваются изотопные ортогональные латинские квадраты. Например, пять попарно ортогональных латинских квадратов 12-го порядка были найдены в результате построения четырех ортоморфизмов абелевой группы, являющейся прямым произведением циклических групп порядков 6 и 2.^[12]

Ко второй группе относятся методы, использующие для построения ортогональных латинских квадратов комбинаторные объекты (включая сами латинские квадраты) меньших порядков. Например, два латинских квадрата 22-го порядка были построены Bose и Shrikhande на основе двух дизайнов 15-го и 7-го порядка.