ГОУВПО «Воронежский государственный технический университет» Факультет энергетики и систем управления Кафедра высшей математики и физико-математического моделирования

Курсовая работа

по дисциплине дискретная математика на тему:

« Исследование Рекуррентного соотношения ряда Фибоначчи »

Выполнил: студент гр. АТР-131 __Фадкин А.В.________________

Принял: доц. Купцов В. С.

Воронеж 2013 г.

Содержание

Условие задачи…………………………………………………………………………….3

Теоретическое введение…………………………………………………………………..4

Решение………………………………………………………………………………… 13

Заключение………………………………………………………………………………19

Список литературы………………………………………………………………………20

Условие задачи

Показать , что любое натуральное число N можно представить в виде суммы чисел Фибоначчи ,причем каждое число входит в сумму не более одного раза , и никакие два соседние числа не входят вместе.

Теоретическое введение

ЧИСЛОВАЯ ПОСЛЕДОВАТЕЛЬНОСТЬ –функциявидаy =f(x),x N, гдеN – множество натуральных чисел (или функция натурального аргумента), обозначаетсяy = f(n) илиy1, y2,…,y_n,…. Значенияy1, y2, y3,… называют соответственно первым, вторым, третьим, … членами последовательности. Рекуррентный способ задания последовательности состоит в том, что указывается правило, позволяющее вычислитьn-й член последовательности, если известны ее предыдущие члены. Название рекуррентный способ происходит от латинского словаrecurrere – возвращаться. Чаще всего в таких случаях указывают формулу, позволяющую выразитьn-й член последовательности через предыдущие, и задают 1–2 начальных члена последовательности.

Пример 1. y1 = 3;y_n = y_n–1 + 4, если n= 2, 3, 4,….

Здесь y1 = 3;y2 = 3 + 4 = 7; y3 = 7 + 4 = 11; ….

Последовательность, составленную в этом примере, специально изучают в математике, поскольку она обладает рядом интересных свойств и приложений. Ее называют последовательностью Фибоначчи – по имени итальянского математика 13 в. Задать последовательность Фибоначчи рекуррентно очень легко, а аналитически – очень трудно. n-е число Фибоначчи выражается через его порядковый номер следующей формулой .

На первый взгляд, формула для n-го числа Фибоначчи кажется неправдоподобной, так как в формуле, задающей последовательность одних только натуральных чисел, содержатся квадратные корни, но можно проверить «вручную» справедливость этой формулы для нескольких первыхn.

Числовую последовательность, каждый член которой, начиная со второго, равен сумме предыдущего члена и одного и того же числа d, называют арифметической прогрессией, а число d – разностью арифметической прогрессии.

Таким образом, арифметическая прогрессия – это числовая последовательность {a_n}, заданная рекуррентно соотношениями

a1 = a, a_n = a_n–1 + d (n = 2, 3, 4, …)

(a и d – заданные числа).

Пример. 1, 3, 5, 7, 9, 11, … – возрастающая арифметическая прогрессия, у которой a1 = 1, d = 2.

Пример. 20, 17, 14, 11, 8, 5, 2, –1, –4,… – убывающая арифметическая прогрессия, у которой a1 = 20, d = –3.

Нетрудно найти явное (формульное) выражение a_n через n. Величина очередного элемента возрастает на d по сравнению с предыдущим, таким образом, величина n элемента возрастет на величину (n – 1)d по сравнению с первым членом арифметической прогрессии, т.е.

a_n = a1 + d(n – 1).

Это формула n-го члена арифметической прогрессии.

Числовую последовательность, все члены которой отличны от нуля и каждый член которой, начиная со второго, получается из предыдущего члена умножением на одно и то же число q, называют геометрической прогрессией, а число q – знаменателем геометрической прогрессии.

Таким образом, геометрическая прогрессия – это числовая последовательность {b_n}, заданная рекуррентно соотношениями

b1 = b, b_n = b_n–1 q (n = 2, 3, 4…).

(b и q – заданные числа, b  0, q  0).

Геометрическая прогрессия является возрастающей последовательностью, если b1 > 0,q> 1, и убывающей, еслиb1 > 0, 0 <q< 1.

Одно из очевидных свойств геометрической прогрессии состоит в том, что если последовательность является геометрической прогрессией, то и последовательность квадратов, т.е. Числовая последовательность является геометрической прогрессией тогда и только тогда, когда квадрат каждого ее члена, кроме первого (и последнего в случае конечной последовательности), равен произведению предыдущего и последующего членов.

Представление натуральных чисел

Любое неотрицательное целое число можно единственным образом представить последовательностьюбитов …ε_k…ε₄ε₃ε₂ () так, что, причём последовательность {ε_k} содержит лишь конечное число единиц, и не имеет пар соседних единиц: . За исключением последнего свойства, данное представление аналогичнодвоичной системе счисления.

Чи́сла Фибона́ччи — элементы числовой последовательности

0, 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144, 233, 377, 610, 987, 1597, 2584, 4181, 6765, 10946,

Иногда число 0 не рассматривается как член последовательности.

Более формально, последовательность чисел Фибоначчи задается линейным рекуррентным соотношением:

Иногда числа Фибоначчи рассматривают и для отрицательных номеров n как двусторонне бесконечную последовательность, удовлетворяющую тому же рекуррентному соотношению. При этом члены с отрицательными индексами легко получить с помощью эквивалентной формулы «назад»: :

n	−10	−9	−8	−7	−6	−5	−4	−3	−2	−1	0	1	2	3	4	5	6	7	8	9	10
	−55	34	−21	13	−8	5	−3	2	−1	1	0	1	1	2	3	5	8	13	21	34	55

Легко заметить, что .

Последовательность Фибоначчи была хорошо известна в древней Индии, где она применялась в метрических науках (просодии, другими словами — стихосложении), намного раньше, чем она стала известна в Европе.Образец длиной n может быть построен путём добавления S к образцу длиной n-1, либо L к образцу длиной n-2; и просодицисты показали, что число образцов длиною n является суммой двух предыдущих чисел в последовательности. Дональд Кнут рассматривает этот эффект в книге «Искусство программирования». На Западе эта последовательность была исследована Леонардо Пизанским, известным как Фибоначчи, в его труде «Liber Abaci» (1202). Он рассматривает развитие идеализированной (биологически нереальной) популяции кроликов, предполагая что: изначально есть новорожденная пара кроликов (самец и самка), со второго месяца после своего рождения кролики начинают спариваться и каждый месяц производить новую пару кроликов, кролики никогда не умирают. Сколько пар кроликов будет через год?

• В начале первого месяца есть только одна новорожденная пара (1).

• В конце первого месяца по-прежнему только одна пара кроликов, но уже спарившаяся (1)

• В конце второго месяца первая пара рождает новую пару и опять спаривается (2)

• В конце третьего месяца первая пара рождает еще одну новую пару и спаривается, вторая пара только спаривается (3)

• В конце четвертого месяца первая пара рождает еще одну новую пару и спаривается, вторая пара рождает новую пару и спаривается, третья пара только спаривается (5)

В конце -го месяца число кроликов будет равно числу кроликов в предыдущем месяце плюс числу новорожденных пар, которых будет столько же, сколько пар было два месяца назад. Таким образом:

Формула Бине выражает в явном виде значение как функцию от n:

где  — золотое сечение. При этом и являются корнями характеристического уравнения .

Из формулы Бине следует, что для всех , есть ближайшее к целое число, то есть . В частности, при справедлива асимптотика .

Формула Бине может быть аналитически продолжена следующим образом:

При этом соотношение выполняется для любого комплексного числа z.

Тождества

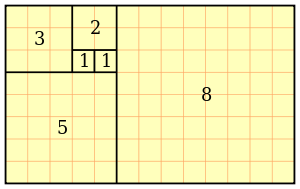
Геометрическое доказательство формулы для суммы квадратов первых n чисел Фибоначчи^[2].

• 

• 

• 

• 

• 

• 

• 

• 

• 

И более общие формулы:

• 

• 

• 

• Числа Фибоначчи представляются значениями континуант на наборе единиц: , то есть

, а также ,

где матрицы имеют размер , i — мнимая единица.

• Числа Фибоначчи можно выразить через многочлены Чебышева:

• Для любого n,

• Следствие. Подсчёт определителей даёт

Свойства

• Наибольший общий делитель двух чисел Фибоначчи равен числу Фибоначчи с индексом, равным наибольшему общему делителю индексов, т. е. . Следствия:

  • делится на тогда и только тогда, когда делится на (за исключением ). В частности, делится на (то есть является чётным) только для ; делится на только для ; делится на только для и т. д.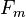

  • может быть простым только для простых (с единственным исключением ). Например, число простое, и его индекс 13 также прост. Обратное не верно, наименьший контрпример — . Неизвестно, бесконечно ли множество чисел Фибоначчи, являющихся простыми.

• Последовательность чисел Фибоначчи является частным случаем возвратной последовательности, её характеристический многочлен имеет корни и .

• Отношения 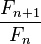являются подходящими дробями золотого сечения и, в частности,

• Суммы биномиальных коэффициентов на диагоналях треугольника Паскаля являются числами Фибоначчи ввиду формулы

.

• В 1964 году Дж. Кон (J. H. E. Cohn) доказал,^[3] что единственными точными квадратами среди чисел Фибоначчи являются числа Фибоначчи с индексами 0, 1, 2, 12:

, , , .

• Производящей функцией последовательности чисел Фибоначчи является:

• Множество чисел Фибоначчи совпадает с множеством неотрицательных значений многочлена

на множестве неотрицательных целых чисел x и y.^[4]

• Произведение и частное двух любых различных чисел Фибоначчи, отличных от единицы, никогда не является числом Фибоначчи.

• Период чисел Фибоначчи по модулю натурального числа n называется периодом Пизано и обозначается π(n). Периоды Пизано π(n) образуют последовательность:

1, 3, 8, 6, 20, 24, 16, 12, 24, 60, 10, 24, 28, 48, 40, 24, 36, … (последовательность A001175

 

в OEIS)

• В частности, последние цифры чисел Фибоначчи образуют периодическую последовательность с периодом π(10)=60, последняя пара цифр чисел Фибоначчи образует последовательность с периодом π(100)=300, последние три цифры — с периодом π(1000)=1500, последние четыре — с периодом π(10000)=15000, последние пять — с периодом π(100000)=150000 и т. д.

• Натуральное число N является числом Фибоначчи тогда и только тогда, когда или является квадратом.^[5]

• Не существует арифметической прогрессии длиной больше 3, состоящей из чисел Фибоначчи.^[6]

• Число Фибоначчи 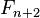равно количеству кортежей длины n из нулей и единиц, в которых нет двух соседних нулей. При этом равно количеству таких кортежей, начинающихся с нуля, а — начинающихся с единицы.

• Особенности чисел Фибоначчи

• 1. каждое третье число Фибоначчи четно;

• 2. каждое четвертое кратно 3;

• 3. каждое пятнадцатое оканчивается нулем;

• 4. два соседних числа Фибоначчи взаимно просты. Ряд Фибоначчи– это не только математическая загадка, мы встречаемся с ним каждый день в повседневной жизни:

• Раковина в форме спирали - форма раковины заинтересовала Архимеда и он выяснил, что увеличение длины завитков раковины – это постоянная величина и равна она 1,618.

• Семена в подсолнухе, в шишке располагаются так же в виде спирали. Пауки плетут свою сеть и стадо на которое нападает хищник, тоже разбегаются по спирали.

• Рост растений тоже происходит в соответствии с числовым рядом Фибоначчи – от ствола отходит ветка, на которой появляется лист, затем происходит длинный выброс и снова появляется листок, но он уже короче предыдущего. Затем опять выброс, но и он короче предыдущего. В этой картине, первый выброс равен 100%, второй 62%, а третий 38%(уровни Фибоначчи, используемые в торговле) и т.д. С длиной лепестков все выглядит точно так же.

• Ящерица – если поделить ящерицу на хвост и тело, то соотношение их будет 0,62 к 0,38.

• Пирамиды – длина ребра пирамиды равна 783.3 футам, а высота пирамиды равна 484.4 футам. Соотношение длины ребра/высота пирамиды составляет 1,618.

«сумма квадратов двух соседних чисел Фибоначчи всегда равна числу Фибоначчи». Эта зависимость описывается формулой [1]:

_Fn2 + (F_{n +1})² = F_2n+1 (3)

и «разность квадратов двух чисел Фибоначчи, номера которых отличаются на два, есть снова число Фибоначчи», описываемая формулой [2]:

F_n+1² – F_n-1² =F_2n (4)

Представим эти зависимости в виде системы формул для нахождения любого заданного числа ряда Фибоначчи.

Запишем ряд Фибоначчи в виде таблицы:

Табл. 1

i	1	2	3	4	5	6	7	8	9	10	11	12	13	14
Fi	1	1	2	3	5	8	13	21	34	55	89	144	233	377

где i - номер числа ряда Фибоначчи;

F_i- - число ряда Фибоначчи.

Представим, например, первые 17 чисел последовательности (1) в виде матрицы определенного вида. В этой матрице числа ряда Фибоначчи записаны по диагонали матрицы. В верхнем горизонтальном и левом вертикальном рядах матрицы записаны квадраты чисел ряда Фибоначчи, расположенные через один промежуток.На пересечении этих чисел (в матрице выделено темным) мы получаем значения чисел ряда Фибоначчи, равное сумме квадратов этих чисел (см. рис. 1). Значит, полученная закономерность описывается формулой (3).

1		12		22		32		52		82		132		212		342
	1
12		2
			3
12				5
					8
22						13
							21
32								34
									55
52										89
											144
82												233
													377
132														610
															987
212																1597

Произведем анализ формулы (3) при различных значениях n = 1, 2, 3, 4, ... . Для этого сведем исходные данные и результаты вычислений формулы (3) в таблицу 2:

n	Сумма квадратов чисел, вычисленных по формуле (3)	Соответствующий номер числа Фибоначчи в таблице 1
1	12 + 12 = 2	3
2	12 + 22 = 5	5
3	22 + 32 = 13	7
4	32 + 52 = 34	9
5	52 + 82 = 89	11

и т. д.

Из таблицы 2 видно, что формула (3) описывает только нечетные числа ряда Фибоначчи.

Произведем анализ формулы (4) при различных значениях n = 1, 2, 3, 4, ... . Для этого сведем исходные данные и результаты вычислений по формуле (4) в таблицу 3:

n	Сумма квадратов чисел, вычисленных по формуле (4)	Номер числа Фибоначчи в таблице 1
2	12- 02= 1	2
3	22- 12= 3	4
4	32- 12= 8	6
5	52-22=21	8
6	82-32= 55	10
7	132- 52= 144	12

Из таблицы 3 следует, что формула (4) описывает только четный ряд чисел Фибоначчи.

Таким образом, обе указанные формулы (3) и (4) совместно описывают весь ряд чисел Фибоначчи. Их можно использовать для нахождения любого заданного числа ряда Фибоначчи:

• нечетные числа ряда Фибоначчи находятся по уравнению:

^Fi(неч) = ^Fn ²+ (^Fn+1)² , ^где i = ²ⁿ + ¹; ⁽⁵⁾

• четные числа ряда Фибоначчи находятся по уравнению:

^Fi (чет) = ^(Fn+1^{)2 - (F}n-1^{)2 , г}д^е 1 = ^{2п , (6)}

где п - натуральный ряд чисел.

Произведем вычисление различных чисел ряда Фибоначчи с помощью полученной системы формул. Задаемся двумя первыми членами чисел Фибоначчи F₁=1 и F₂ = 1, поскольку «для однозначного построения последовательности формулы недостаточно, и необходимо указать дополнительные условия, например, задать несколько первых членов последовательности» [2].

При помощи формул (5) и (6) произведем вычисление некоторых членов ряда Фибоначчи, начиная с третьего.

Вычислим третий член ряда Фибоначчи - F₃, т.е. i = 3. Это нечетный член, поэтому в

соответствии с формулой (5) i = 2n +1. Тогда 3 = 2n +1, откуда n = 1.

F₃= F₁² + (F1+1)² = 1² +1² = 2, что как видно из табл. 1, соответствует действительности.

Вычислим четвертый член ряда Фибоначчи - F₄, т.е. i = 4. Это четный член, поэтому в

соответствии с формулой (6) i = 2n . Тогда 4 = 2п, откуда n = 2.

F₄ = (F₂₊₁)² - (F_2-1)² =F₃² – F₁² = 2² -1² = 3, что как видно из табл. 1, соответствует действительности.

Вычислим пятый член ряда Фибоначчи - F₅, т.е. i = 5. Это нечетный член, поэтому в соответствии с формулой (5) i = 2n +1. Тогда 5 = 2n +1, откуда n = 2.

F5 = F₂ ² + (F2+1) ² = F2 ² + F₃² = 1² + 2² = 5, что как видно из табл. 1, соответствует действительности.