72

3.6.ОСОБЕННОСТИ РАСЧЕТА КОНИЧЕСКИХ ЗУБЧАТЫХ ПЕРЕДАЧ

3.6.1.ОБЩИЕ СВЕДЕНИЯ

Впередачах, в которых оси валов пересекаются под некоторым углом ∑,

применяют конические зубчатые колеса. Наиболее распространены передачи с углом ∑=90°.

Конические передачи сложнее цилиндрических в изготовлении и монтаже. Для нарезания конических колес требуются специальные станки и инструмент. Выполнить коническое зацепление с той же степенью точности, что и цилиндрическое, значительно труднее. Одно из конических колес, как правило, располагают консольно. При этом увеличивается неравномерность распределения нагрузки по длине зуба. В коническом зацеплении действуют осевые силы, наличие которых усложняет конструкцию опор. Все это приводит к тому, что, по опытным данным, нагрузочная способность конической прямозубой передачи составляет лишь около 85% цилиндрической. Однако, несмотря на очевидные недостатки, конические передачи имеют широкое применение в тех случаях, когда по условиям компоновки машин и механизмов необходимо располагать валы под углом.

73

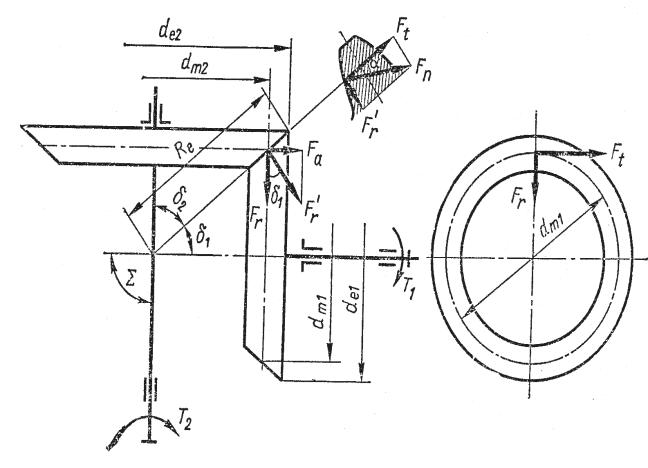
Геометрические параметры. Аналогами начальных и делительных цилиндров цилиндрических передач в конических передачах являются начальные и делительные конусы с углами δ1 и δ2. Конусы, образующие которых перпендикулярны образующим делительных конусов, называют дополнительными конусами. Сечение зубьев дополнительным конусом называют торцовым сечением. Размеры, относящиеся к внешнему торцовому сечению, сопровождают индексом е, например, de, Re и др. Размеры в среднем сечении сопровождают индексом m : dm, Rm. Эти и остальные параметры показаны на рис.

Рис. 3.17

3.17.

В основу расчета конических передач положены формулы для определения контактных σΗ (3.9) и изгибных σF1 и σF2 (3.14) напряжений цилиндрических колес, в которых некоторые параметры заменены на эквивалентные, отражающие особенности конических передач.

74

Для эквивалентных цилиндрических колес числа их зубьев определяются по формулам

zvt1 = cosz1δ1 ; zvt 2 = cosz2δ2 ,

где z1 и z2 – числа зубьев конических колес; δ1 и δ2 – углы делительных конусов конических колес (как правило выполняется условие δ1 + δ2 = 90° ).

Передаточные отношения, при δ1 + δ2 = 90° можно представить i12 = u = z2/z1 = d2/d1.

3.6.2.СИЛЫ В ЗАЦЕПЛЕНИИ ПРЯМОЗУБОЙ КОНИЧЕСКОЙ ПЕРЕДАЧИ

Взацеплении конической передачи действуют силы окружная Ft,

радиальная Fr и осевая Fa. Зависимость между этими силами можно установить с помощью рис. 3.17, где силы изображены приложенными к шестерне.

По нормали к зубу действует сила Fn, которую раскладывают на Ft и Fr1 . В

свою очередь, Fr1 раскладывают на Fa и Fr. Тогда силы равны

Приведение прямозубого конического колеса к эквивалентному прямозубому цилиндрическому. Параметры эквивалентных колес используют при расчете на прочность.

Диаметры эквивалентных колес

Числа зубьев эквивалентных колес

Тогда основные расчетные формулы для конической передачи будут выглядеть следующим образом:

для расчета по критерию контактной прочности σΗ ≤ [ σΗ ] :

Формулы (3.35) и (3.36) после подстановки конкретных значений некоторых параметров, а также ряда преобразований можно представить в виде более удобном для практического применения

Здесь коэффициенты формы зубьев Υvt1 и Υvt2 выбираются соответственно для zv1 и zv2; dm1 = z1 mm – средний делительный диаметр конической шестерни.

В приведенных формулах учтено, что на основании экспериментальных данных конические колеса могут нести нагрузку на 15% меньшую, чем цилиндрические таких же размеров.

Рекомендации по определению коэффициентов KHβ (KFβ) и KHV (KFV),

входящих в формулы (3.37) и (3.38) даны в работах [ 2,4 ].