Мокроусов_ПЗ_КМЗИ

Решение этой задачи иногда существует, а иногда его нет. Например, обратная величина для числа 5 по модулю 14 равна 3, поскольку

5*3=15 1 (mod 14).

С другой стороны, число 2 не имеет обратной величины по модулю 14.

Вообще сравнение a-1 x (mod n) имеет единственное решение, если а и n - взаимно простые числа.

Если числа а и n не являются взаимно простыми, тогда сравнение a-1 x ( mod n ) не имеет решения.

Сформулируем основные способы нахождения обратных величин. Пусть целое число aє{0, 1, 2, ..., n -1}. Если НОД (а, n) = 1, то a * i (mod n) при i = 0, 1, 2, ..., n-1 является перестановкой множества {0, 1, 2, ..., n -1}.

Например, если а = 3 и n = 7(НОД (3,7)=1), то

3 * i ( mod 7) при i = 0, 1, 2, ..., 6

является последовательностью 0, 3, 6, 2, 5, 1, 4, т. е. перестановкой множества {0, 1, 2 .... 6}.

Это становится неверным, когда НОД (а, n)≠1. Например, если а = 2 и n =6, то

2 * i ( mod 6) 0, 2, 4, 0, 2, 4 при i = 0, 1, 2, ..., 5.

Если НОД (а, n)=1, тогда существует обратное число а- 1, 0<а-1<n , такое, что

а * а-1 1(mod n).

Действительно, a * i (mod n) является перестановкой 0,1, ..., n-1, поэтому существует i, такое, что

а * i 1(mod n).

9

Как уже отмечалось, набор целых чисел от 0 до n-1

называют полным набором вычетов по модулю n. Это означает, что для любого целого числа а (а>0) его вычет r=a (mod n) - это некоторое целое число в интервале от 0

до n-1.

Выделим из полного набора вычетов подмножество вычетов, взаимно простых с n . Такое подмножество называют приведенным набором вычетов.

Пример. Пусть модуль n = 11 - простое число. Полный набор вычетов по модулю 11

{0, 1, 2, ..., 10}.

При формировании приведенного набора вычетов из них удаляется только один элемент - 0. Приведенный набор вычетов по модулю 11 имеет 11-1=10 элементов.

Вообще приведенный набор вычетов по модулю простого числа n имеет n-1 элементов.

Пример. Пусть модуль n =10. Полный набор вычетов по модулю n =10

{0, 1, 2, 3, 4, 5, 6, 7, 8, 9}.

Из них только 1, 3, 7, 9 не имеют общего сомножителя с числом 10. Поэтому приведенный набор вычетов по модулю 10 равен {1, 3, 7, 9}. При формировании этого приведенного набора были исключены элементы:

0 (1 элемент) кратные 2 (4 элемента) кратные 5 (1 элемент),

т. е. всего шесть элементов. Вычитая их из 10, получаем 10-1-4-1=4, т. е. четыре элемента в приведенном наборе.

10

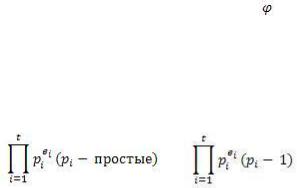
Для произведения простых чисел p*q=n приведенный набор вычетов имеет (р - 1)(q - 1) элементов. При n = p*q = = 2*5= 10 число элементов в приведенном наборе

(р-1)(q-1) = (2-1)(5-1) = 4.

Пример. Приведенный набор вычетов по модулю 27= 33 имеет 18 элементов:

{1, 2, 4, 5, 7, 8, 10, 11, 13, 14, 16, 17, 19, 20, 22, 23, 25, 26}.

Из полного набора вычетов исключены элементы, кратные 3 (всего девять элементов). Для модуля в виде простой степени nr приведенный набор вычетов имеет nr-1 1(n-1) элементов.

При n = 3, r = 3 получаем З3-1(3-1)=32 *2=18.

Функция Эйлера 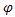(n) характеризует число элементов в приведенном наборе вычетов (табл. 3).

Таблица 3

Функция Эйлера

Иначе говоря, функция (n) - это количество положительных целых, меньших n, которые взаимно просты с n.

11

Малая теорема Ферма: если n - простое и НОД (а, n) = 1,

то

an-1 1(mod n).

Согласно обобщению Эйлером малой теоремы Ферма имеем: если НОД (а, n)= 1, то

a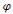(n) 1(mod n).

Если n - простое число, то предыдущий результат, учитывая , что 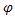(n) = n-1, приводится к виду (малой теоремы Ферма)

an-1 1(mod n).

Основные способы нахождения обратных величин

a-1 1( mod n).

•Проверить поочередно значения 1, 2 ,..., n -1, пока не будет найден a-1 1(mod n), такой, что a*a-1 (mod n) 1 .

•Если известна функция Эйлера (n), то можно вычислить

a-1(mod n) a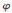(n)-1 (mod n),

используя алгоритм быстрого возведения в степень.

3. Если функция Эйлера (n) не известна, можно использовать расширенный алгоритм Евклида.

Проиллюстрируем эти способы на числовых примерах . 1. Поочередная проверка значений 1, 2, ..., n-1, пока не

будет найден x=a-1 (mod n), такой что a * x 1(mod n). Пусть n = 7, а = 5. Требуется найти x = a-1 (mod n).

a*x 1(mod n) или 5*x 1 (mod 7).

12

n-1 = 7-1 = 6.

Получаем x = 5-1 (mod 7) = 3.

Результаты проверки сведены в табл. 4.

Таблица 4

Результаты проверки

2.Нахождение a-1 (mod n), если известна функция

Эйлера 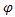(n).

Пусть n=7, а=5. Найти x = a-1 (mod n) = 5-1 (mod 7).

Модуль n=7 - простое число. Поэтому функция Эйлера (n) =(7) = n-1=6. Обратная величина от 5 по mod 7

a-1 (mod n) = a(n)-1(mod n) = 56-1 mod 7 = 55 mod 7 =

= (52 mod 7)(53 mod 7) mod 7 = (25 mod 7)(125 mod 7) mod 7 = (4 * 6) mod 7 = 24 mod 7= 3.

Итак, x =5-1 (mod 7) = 3.

3. Нахождение обратной величины a-1 (mod n) с помощью расширенного алгоритма Евклида.

Алгоритм Евклида можно обобщить способом, который имеет большое практическое значение. При этом способе во время вычисления НОД (а, b) можно попутно вычислить такие целые числа u1, и u2, что

а * u1 + b * u2 = НОД (a, b).

13

Это обобщение (расширение) алгоритма Евклида удобно описать, используя векторные обозначения.

Контрольные вопросы:

1.Что такое мультипликативная обратная величина?

2.Что такое полный набор вычетов по модулю?

3.В чём смысл малой теоремы Ферма?

4.Привести примеры различных функций шифрования.

5.Приведите примеры криптосистем. Что называется числовым эквивалентом элемента открытого кода?

6.Что называется поалфавитным шифрованием?

7.Что называется полиалфавитным шифрованием?

8.Могут ли одному и тому элементарному сообщению соответствовать различные шифры?

14

Практическое занятие № 4 Квадратичные вычеты

Рассмотрим некоторое простое р>2 и число а<р [2]. Если число а сравнимо с квадратом некоторого числа х по модулю р, т. е. выполняется сравнение x2 a (mod p), тогда а называют квадратичным вычетом по модулю р. В противном случае а называют квадратичным невычетом по модулю р.

Если а - квадратичный вычет, сравнение x2 a (mod p) имеет два решения: + х и - х, т.е. а имеет два квадратных корня по модулю р.

Все квадратичные вычеты находят возведением в квадрат элементов 1, 2, 3, ..., (р-1)/2.

Не все значения а<р являются квадратичными вычетами. Например, при р=7 квадратичные вычеты это 1, 2, 4:

12 =1 1(mod 7),

22 = 4 4(mod 7),

32 = 9 2(mod 7),

42 = 16 2(mod 7),

62 = 36 1(mod 7).

Заметим, что каждый квадратичный вычет появляется в этом списке дважды. Не существует никаких значений х, которые удовлетворяли бы любому из следующих уравнений:

x2 3(mod 7), x2 5(mod 7), x2 6(mod 7).

Числа 3, 5 и 6 - квадратичные невычеты по модулю 7. Можно доказать, что существует точно (р -1)/2 квадратичных вычетов по модулю р и (р-1)/2 квадратичных невычетов по модулю р.

Если а - квадратичный вычет по модулю р, то а имеет точно два квадратных корня: один корень между 0 и (р-1)/2, другой корень между (р-1)/2 и (р-1).

15

Один из этих квадратных корней также является квадратичным вычетом по модулю р; он называется главным квадратным корнем.

Пример. Вычисление квадратных корней при р=7 представлено в табл. 5.

Если n - произведение двух простых р и q, т. е. n = p * q, то существуют точно

(p-1)(q-1)/4

квадратичных вычетов по модулю n, взаимно простых с n. Например, по модулю 35 (р=5, q=7, n=5*7=35) существуют

(5-7)(7-1)/4 = 4*6/4 = 6

квадратичных вычетов: 1, 4, 9, 11, 16, 29, взаимно простых с 35.

Контрольные вопросы:

1.Что такое квадратичный невычет по модулю?

2.Как находят квадратичные вычеты?

3.Что такое главный квадратный корень?

4.Привести примеры односторонних функций с секретом и без него.

5.Привести пример шифрования данных, устойчивого относительно арифметических ошибок вида +2i (-2i).

6.Привести примеры систем маскировки.

7.Определить криптостойкость способа шифрования

сэлементом маскировки.

16

Практическое занятие № 5 Китайская теорема об остатках

Любое неотрицательное целое число, не превосходящее произведения модулей, можно однозначно восстановить, если известны его вычеты по этим модулям [2]. Этот результат был известен еще в древнем Китае и носит название китайской теоремы об остатках. Теорема была предложена китайским математиком первого века Сун Це. Китайская теорема об остатках является мощным криптографическим инструментом.

Китайская теорема об остатках формулируется следующим образом.

Пусть m1, m2, ..., mt - модули (целые числа, большие 1), которые являются попарно взаимно простыми, т.е. HOД (mi, mj)=1 при i ≠ j .

Пусть a1, a2, ..., at - тоже целые числа, 0 ≤ ai ≤ mi.

Пусть M = m1 * m2 *...* mt – произведение всех mi. Обозначим Мi = М /mi

И пусть Ni будет обратным к Mi (mod mi), i=1, 2, ..., t,

т.е. Mi * Ni 1(mod mi).

Так как HOД (Mi, mi) = 1, то обратный элемент Ni существует и легко находится из алгоритма Евклида из соотношения

Mi * Ni + mi * n i = 1, i = 1, 2, ..., t.

Сравнения x ai (mod mi), i = 1, 2, ..., t, имеют в интервале [0, М-1] единственное общее решение

x= ai * Ni * Mi (mod M).

Рассмотрим частный случай. Пусть M = m1 * m2, где m1, m2 – взаимно простые числа. Тогда для произвольных целых a1< m1 и a2<m2 существует единственное число х, х<М, такое, что

х a1(mod m1) и x = a2 (mod m2).

17

Чтобы найти значение решения х, сначала используют алгоритм Евклида для вычисления значений Ni и N2, таких, что

N1 * M1 1 (mod m1) и N2 * М2 1 (mod m2).

Здесь M1 = M / m1 = m1* m2 / m1= m2, M2 = M / m 2 = m1

Затем вычисляют значение

x = (a1* N1* M1 + a2* N2* M2)(mod M).

Пример. Решить систему из двух сравнений

x1(mod 5),

х10 (mod 11)

инайти общее решение х по модулю 55. Здесь m1= 5; m1= 11;

M=m1* m2 = 5*11=55; a1 = 1; a2=10; M1= M/m1=m2=11; M2=M/m2=m1=5.

Найдем значения N1 и N2, обратные к M1 и M2

соответственно по mod m1 и - mod m2:

M1* N1 1 (mod m1), 11*N1 1(mod 5) => N1 = 1, M2* N2 1(mod m2), 5 * N2 1 (mod 11) => N2 = 9.

Вычисляем общее значение

x = (a1M1N1 + a2M2N2)(mod N) =

=(1 * 11 * 1 + 10 * 5 * 9)(mod 55) =

=(11 + 450)(mod 55) = 461 (mod 55) = 21 (mod 55).

Итак, x=21(mod 55).

Контрольные вопросы:

1.Как можно восстановить любое неотрицательное целое число, не превосходящее произведения модулей?

2.Как формулируется китайская теорема об остатках?

18