1.2. Расчетные формулы для определения параметров передаточной функции двигателя

Все вычисления параметров двигателя постоянного тока приводятся с точностью до 0,0001.

Параметры передаточной функции двигателя – таблица 4.

Ток двигателя

Электромагнитный момент

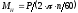
Константа

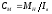
Константа

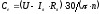
Электромеханическая постоянная времени

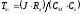
Электромагнитная постоянная времени

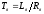
Коэффициент передачи двигателя по управлению

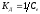
Таблица 4 - Параметры передаточной функции двигателя

Iя	Mн	Cм	Ce	Tm	Tя	Kд
3.0992	4.0539	1.3081	1.8404	0.0316	0.0146	0.5434

2. Дифференциальные уравнения электромеханической системы.

2.1. Классическая форма записи дифференциального уравнения двигателя.

Система уравнений, описывающих работу двигателя, сводится к единому уравнению, где в качестве переменных две величины: U_H(t) и ω_вр(t).

(2.1)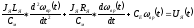

Разделим обе части уравнения (2.1) на величину С_e и введем константы Т_м, Т_a и К_Д

(2.2)

Блок регулируемого электропривода (БРП, см Рис. 1) состоит из предварительного усилителя (ПУ2) и усилителя мощности (У). Усилитель мощности представляет собой апериодическое звено первого порядка с коэффициентами К_У и Т_У. Предварительный усилитель (ПУ2) – пропорциональное звено с коэффициентом передачи К_ПУ2 (см табл. 2).

Уравнение усилителя мощности:

(2.3)

(2.4)

Предварительный усилитель (ПУ1, см Рис. 1) представляет собой пропорциональное звено с коэффициентом передачи К_ПУ1. Уравнение предварительного усилителя (ПУ1):

Редуктор представляет собой интегрирующее звено и служит для преобразования скорости вращения вала двигателя ω_дв(t) в угол поворота φ_p(t).

Уравнение редуктора:

(2.5)

Тахогенератор – устройство для измерения скорости вращения. Напряжение на выходе тахогенератора U_вых(t) пропорционально скорости вращения ω_вр(t).

(2.6)

Датчик угла поворота (Д.О.С.). Напряжение на выходе Д.О.С. U_вых(t) пропорционально углу поворота φ_р(t):

(2.7)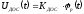

2.2. Уравнения состояний системы управления и двигателя.

По полученной структурной схеме запишем уравнения состояния системы управления:

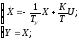
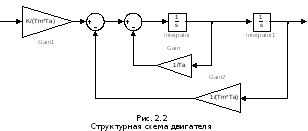Воспользуемся теми же преобразованиями для составления уравнений состояния двигателя, представленного типовым динамическим звеном второго порядка.

По полученной структурной схеме запишем уравнения состояния двигателя:

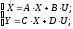
где

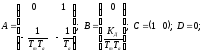
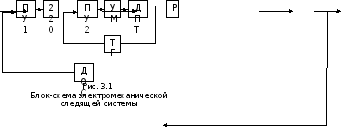3. Структурные схемы электромеханической следящей системы

3.1. Блок-схема электромеханической следящей системы

3.2. Структурная схема САР скорости с развернутой структурной схемой двигателя

Рис. 3.2.

Структурная схема электромеханической следящей системы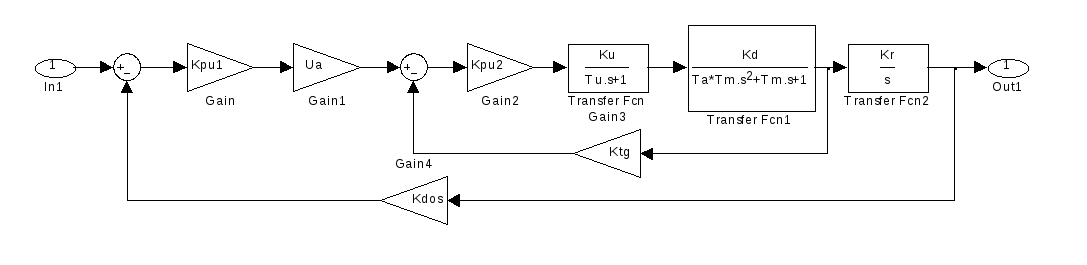

3.3. Структурная схема электромеханической следящей системы с свернутой структурной схемой двигателя

Рис. 3.3.

САР скорости электромеханической следящей системы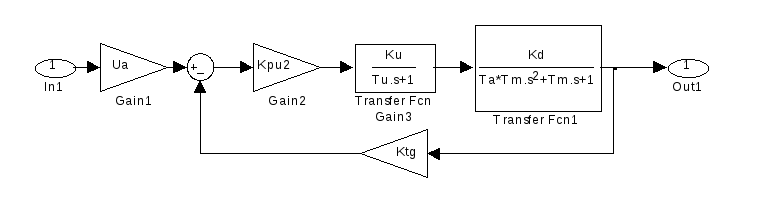

4. Анализ электромеханической системы

4.1. Анализ устойчивости

4.1.1 Анализ устойчивости по характеристическому уравнению

Характеристическое уравнение системы 4го порядка:

где:

,

,

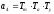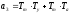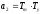
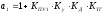
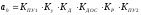
Для моего варианта:

, ,,,

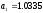Условия устойчивости: 1) 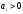, 2)

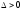
Определитель Гурвица:

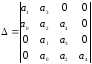
a1*a2*a3-a0*(a3^2)-(a1^2)*a4;

Так как Δ<0,то система неустойчивая.

Все исследования проводятся в рабочей области с использованием следующих операторов:

h1=tf(Kd,[Tm*Ta Tm 1]);

h2=tf(Ku,[Tu 1]);

h3=tf(Kpu);

h4=tf(Ktg);

h5=tf(220);

h6=tf(Kpu);

h7=tf(Kr,[1 0]);

hsr=feedback(h1*h2*h3,h4);

hssr=h5*h6*h7*hsr;

g=feedback(hssr,Kdos);

4.1.2. Анализ устойчивости по корням характеристического уравнения

>> pole(g)

Уравнение имеет 4 корня:

-43.8950 +33.6144i

-43.8950 -33.6144i

2.9716 +23.2060i

2.9716 -23.2060i

Т.к. имеются отрицательные действительные части в корнях, система является неустойчивой.

4.1.3. Анализ устойчивости по распределению корней

>> pzmap(g)

Рис. 4.

Расположение корней на комплексной плоскости

Из Рис. 4. видно, что система неустойчива. Ее параметры определить невозможно.

4.1.4. Анализ устойчивости по АФЧХ

>> nyquist(hssr)

Рис. 5.

Характеристика nyquist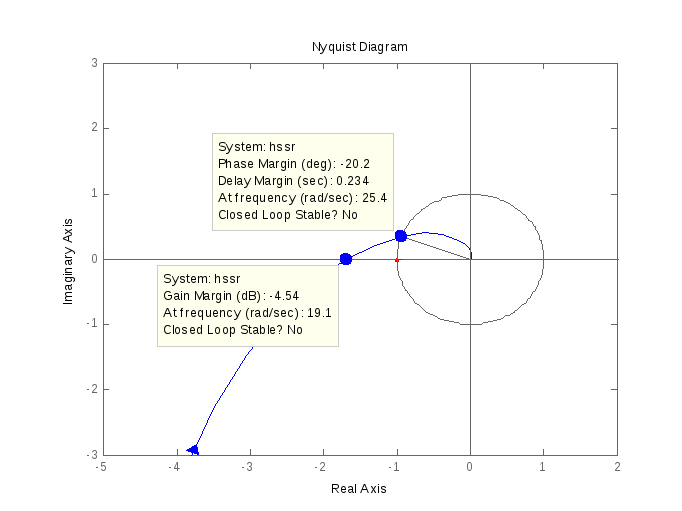

На рис 5. представлена АФЧХ разомкнутой системы. Т.к текущий угол больше 180°,то система неустойчива.

4.1.5. Анализ устойчивости по ЛАЧХ и ЛФЧХ разомкнутой системы

>> bode(hssr)

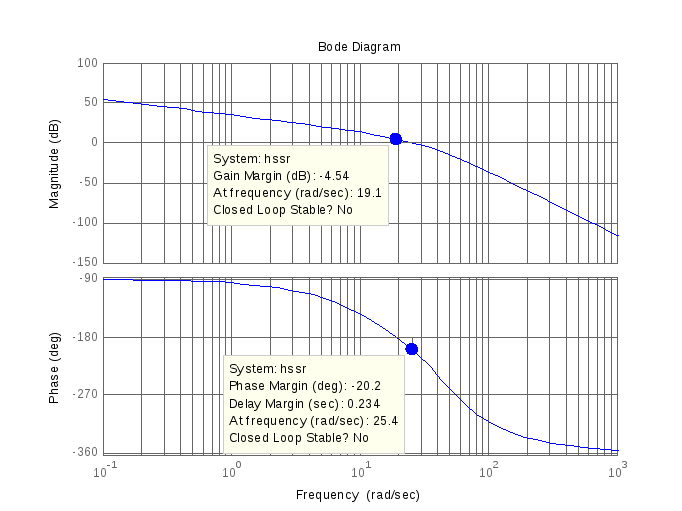
Рис. 6.

ЛАЧХ и ЛФЧХ разомкнутой системы

На рис. 6 показаны запасы по амплитуде и запас по фазе. Т.к. ∆L>0, то система неустойчива

4.2. Анализ показателей качества САР скорости и СС

4.2.1. Анализ показателей качества САР скорости

По условиям работы САР скорости должна иметь h_уст= 1060 [об/мин]

>> hsr0=220*hsr

>>step(hsr0)

Рис. 7.

График переходной характеристики САР скорости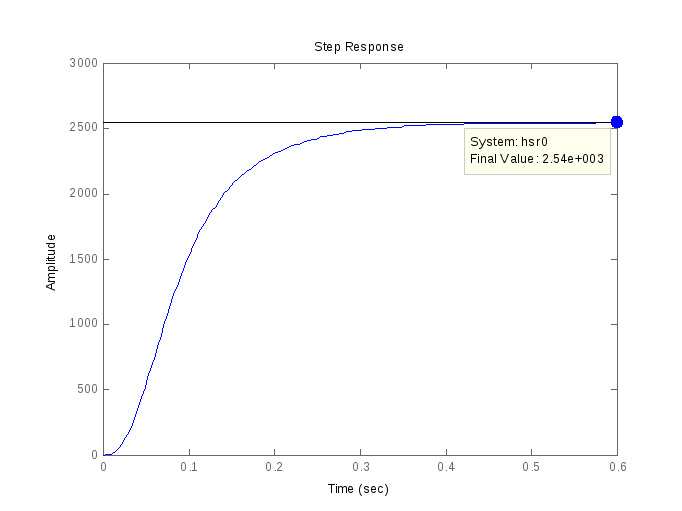

Из рис. 7. Видим, что не равняется заданной частоте вращенияn= 1060 об/мин.

Подбираем коэффициент К_пу2:

>>h3=tf(0.899)

>>hsr=feedback(h1*h2*h3,h4)

>>hsr0=220*hsr

>>step(hsr0)

Получаем график ПХ САР скорости в соответствии с заданными параметрами регулирования (Рис. 8.): h_уст = n = 1060 об/мин; К_пу2 = 0.899;

Рис. 8.

ПХ настроенной САР