
- •9.4. Обратная связь по производной от скорости исполнительного вала 32
- •9.5. Обратная связь по второй производной от скорости исполнительного вала или по разности скоростей 33
- •9.6. Обратная связь по производной от скорости двигателя 34
- •1. Техническое задание.
- •2. Исходные данные.
- •Введение
- •3. Выбор электродвигателя.
- •4. Трехмассовая упругая система.
- •5. Приведение к двухмассовой системе.
- •6.Математическая модель электромеханической системы подчинённого управления с упругой механической связью
- •7 Анализ статического и динамического режима работы электромеханической системы электропривода
- •8.2. Настройка контура скорости на симметричный оптимум.
- •8.3 Моделирование одномассовой системы со стандарными настройками.
- •9 Двухмассовая система
- •9.1. Моделирование двухмассовой системы со стандартными настройками.
- •9.2. Настройкаэлектромеханической системы с учётом упругости. Настройка двухмассовой системы без применения корректирующих устройств.
- •9.3 Настройка двухмассовой системы с корректирующими устройствами
- •9.4. Обратная связь по производной от скорости исполнительного вала
- •9.5. Обратная связь по второй производной от скорости исполнительного вала или по разности скоростей
- •9.6. Обратная связь по производной от скорости двигателя
- •10. Исследование влияния нелинейности на работу двухмассовой системы.
- •11. Заключение
- •11.Список используемой литературы.
7 Анализ статического и динамического режима работы электромеханической системы электропривода
7.1 Расчетные параметры тиристорного преобразователя
Коэффициент усиления силового преобразователя:
Ктп
=
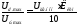 ,
,
Ктп
=
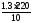 = 28.6;
= 28.6;
где
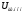 -
номинальное напряжение двигателя,
-
номинальное напряжение двигателя,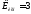 -
коэффициент использования двигателя
-
коэффициент использования двигателя
Постоянная времени преобразователя принимается равной Ттп = 0,01 с.
7.2 Расчет коэффициентов передачи датчиков обратной связи
Коэффициент передачи датчика тока:
Кост
=
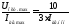 ,
,
Кост
=
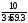 = 0,067 В /A.
= 0,067 В /A.
Коэффициент передачи датчика скорости:
Косс
=
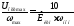 ,
,
Косс
=
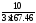 = 0,021 Вc
/ рад
= 0,021 Вc
/ рад
8 Стандартные настройки одномассовой системы.
Расчет динамических характеристик системы электропривода, настроенной на технический оптимум
8.1 Контур тока якоря

Рис.6 Структурная схема контура тока
В практике проектирования систем подчиненного управления электроприводами широкое применение находят стандартные настройки регулирования. Передаточная функция регулятора Wрег(p):
 (8.1)
(8.1)
Где
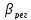 - коэффициент усиления регулятора;
- коэффициент усиления регулятора;
 -
постоянная времени регулятора.
-
постоянная времени регулятора.
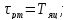 (8.2)
(8.2)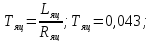
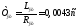 (8.3)
(8.3)
где
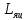 - индуктивность якорной цепи;
- индуктивность якорной цепи;
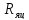 -
сопротивление якорной цепи.
-
сопротивление якорной цепи. 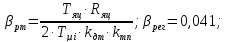
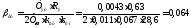 (8.4)
(8.4)
где
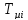 - малая постоянная времени токового
контура;
- малая постоянная времени токового
контура;
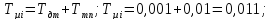 (8.5)
(8.5)
 –соответственно,
постоянная времени датчика тока и
тиристорного преобразователя.
–соответственно,
постоянная времени датчика тока и
тиристорного преобразователя.
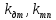 –соответственно,
коэффициент усиления датчика тока и
тиристорного преобразователя.
–соответственно,
коэффициент усиления датчика тока и
тиристорного преобразователя. 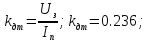
Согласно передаточной функции (6.1) составим, передаточная функция контура тока будет выглядеть следующим образом:

 (8.6)
(8.6)
Техническая реализация выражения (6.8) возможна при помощи схемы, представленной на рис.
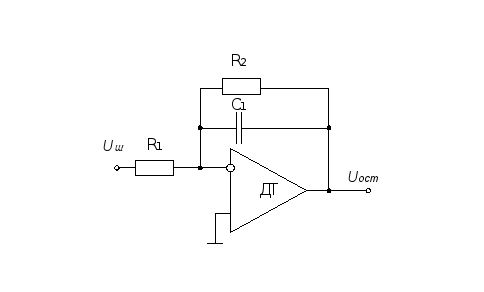
Реализация контура тока в Matlab показана на рис.
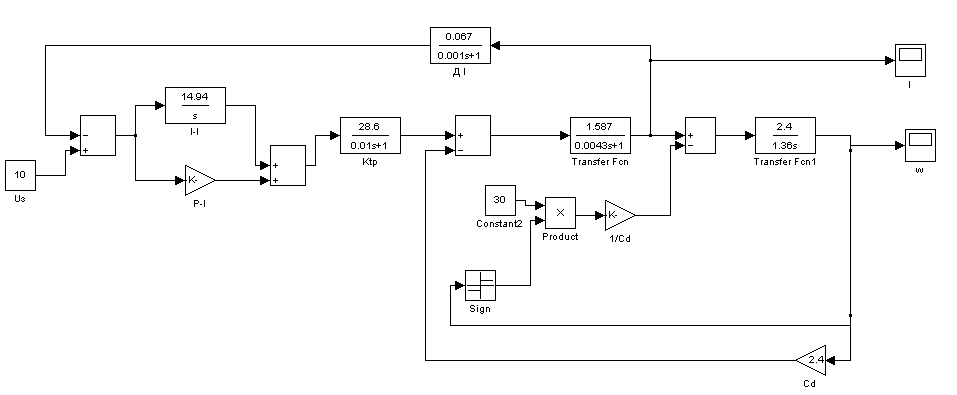
Рис.8 Реализация контура тока в Matlab
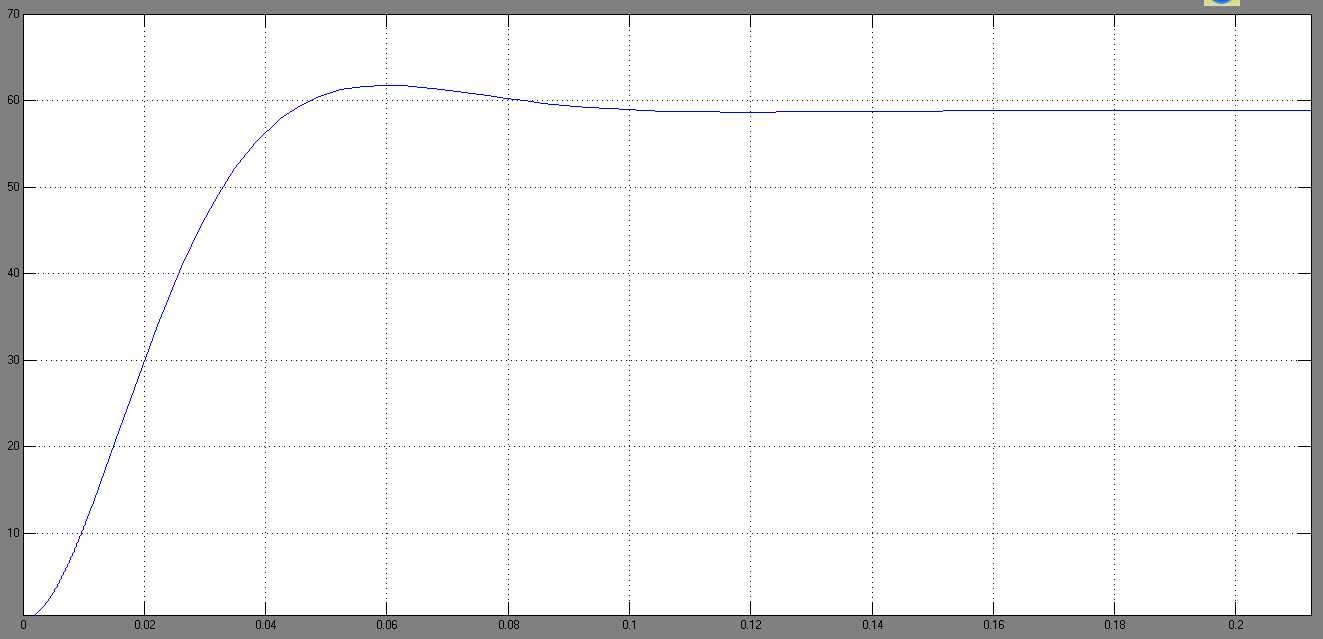
Рис.9 Переходная характеристика по току при настроике контура тока на модульный оптимум
Как видно из рисунка величина перерегулирования составляет 4,3%.
8.2. Настройка контура скорости на симметричный оптимум.
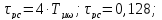 (8.7)
(8.7)
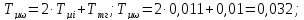 (8.8)
(8.8)
где
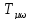 - малая постоянная времени контура
скорости;
- малая постоянная времени контура
скорости;
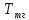 -
постоянная времени тахогенератора;
-
постоянная времени тахогенератора;
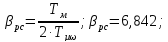
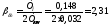 (8.9)
(8.9) 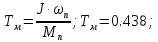
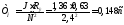 (8.10)
(8.10) 
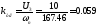 (6.13)
(6.13)
где
 – механическая постоянная времени;
– механическая постоянная времени;
 -
коэффициент усиления тахогенератора;
-
коэффициент усиления тахогенератора;
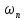 -
номинальная частота вращения двигателя.
-
номинальная частота вращения двигателя.
Передаточная функция контура скорости будет иметь вид:
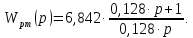
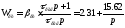 (8.11)
(8.11)
Техническая реализация выражения (6.14) возна при помощи схемы, представленной на рис.
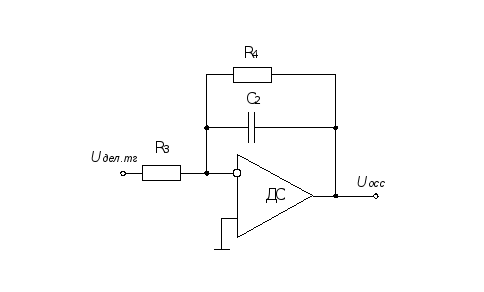
Применеие симметричного оптимума для насройки контура скорости связано с необходимостью уменьшения пусковых токов в контуре тока; применение для контура скорости модального оптимума приводит к превышению пусковым током 10 номинальных значений, что недопустимо.
8.3 Моделирование одномассовой системы со стандарными настройками.
Ниже на рис.11 приведена структурная схема системы двухконтурного управления одномассового ЭП на основе ДПТ НВ. 1- ЭМ и М элементы ДПТ НВ, 2- модель нагрузки (Мс), 3- тиристорный преобразователь, 4-ПИ регулятор тока, 5-контур тока якоря, 6-ПИ регулятор контура скорости, 7- контур скорости.
На рис.12 Приведены графики переходных процессов в системе по току и скорости. Из них видно, что величина перерегулировния требуемого параметра- скорости на валу двигателя не привышает величины 5 %, при этом величина броска тока при пуске соответсвует перегрузочной способности данной машины.
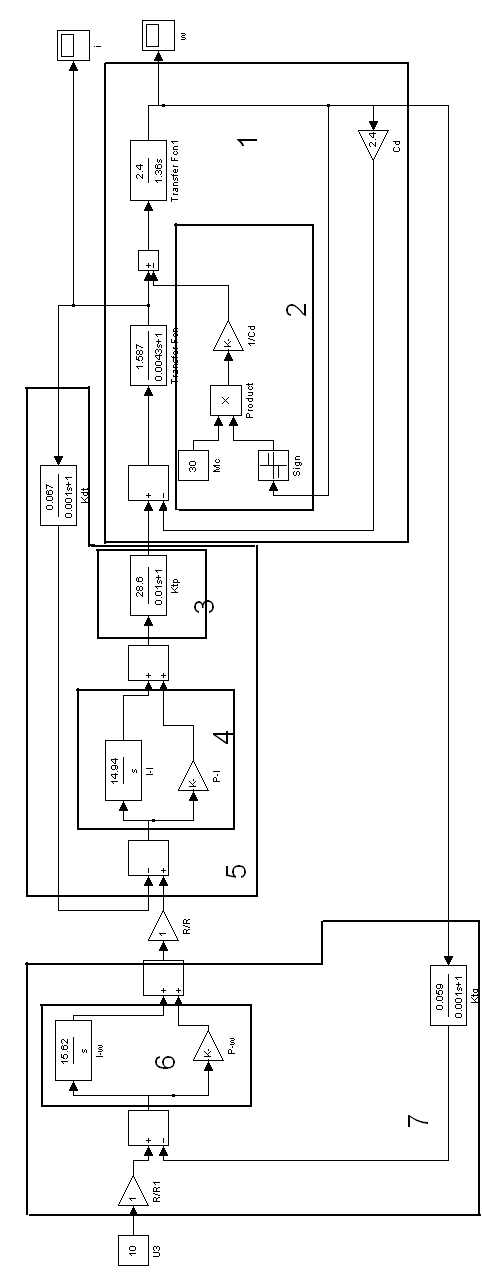
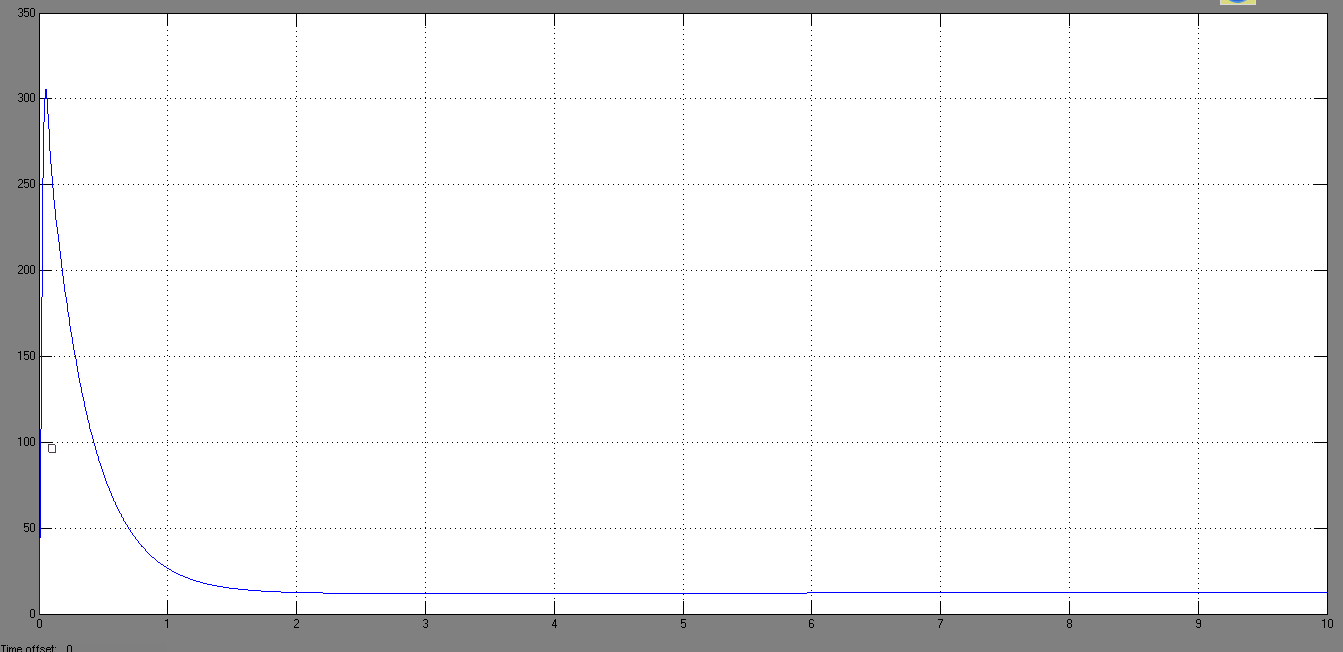
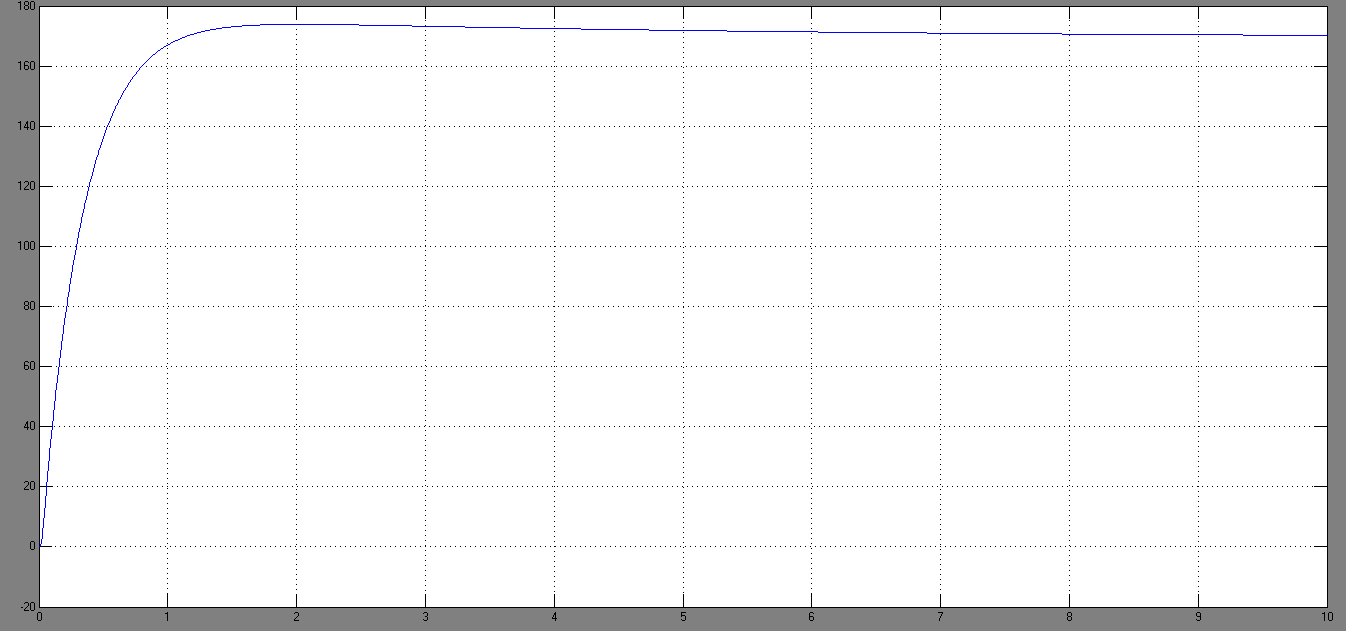
Рис.12 Графики переходных процессов в системе по току и скорости.
Далее представим систему в нормированном виде, для чего воспользуемся структурной схемой рис.4б. При этом:
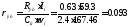 ;
;
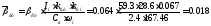

Тогда схема системы приобретёт вид, показанный на рис.13. Переходные характеристики нормированных величин тока и скорости показаны на рис.14.
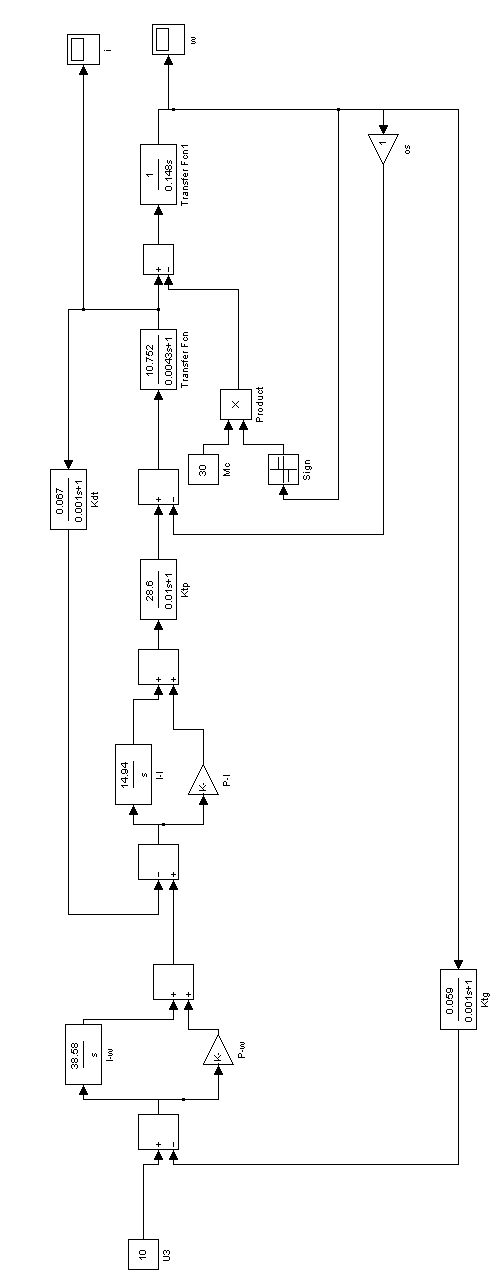
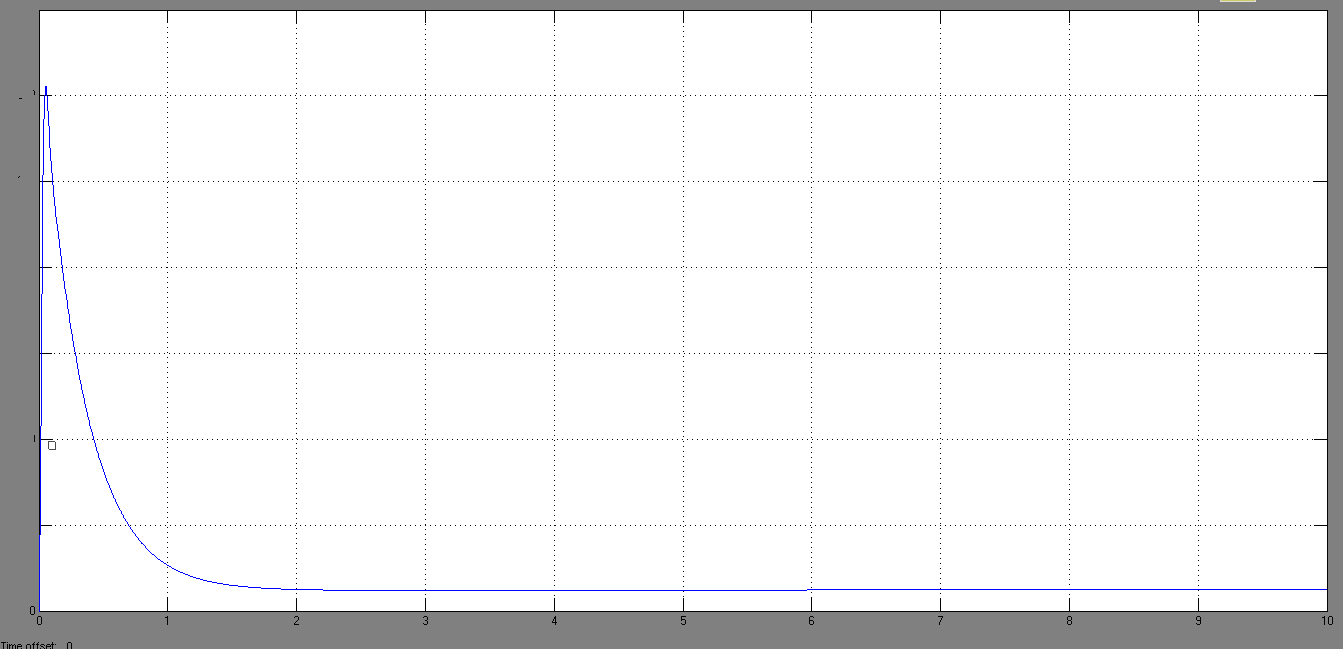

Рис.14 Переходные характеристики нормированных величин тока и скорости
