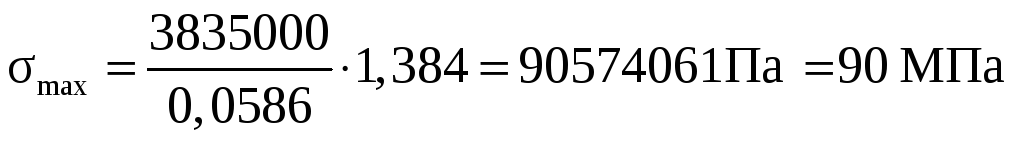- •1 Компоновка самолёта
- •Iряд – число рядов кресел;
- •4.1 Расчёт центровки в снаряжённом состоянии
- •5 Нагрузки, действующие на фюзеляж
- •6 Определение реакций, действующих на фюзеляж от крыла
- •10 Построение эпюр qу и mz
- •11 Предварительное проектирование силового набора фюзеляжа
- •12 Проектировочный расчет трех сечений фюзеляжа
- •15 Расчет типового шпангоута
10 Построение эпюр qу и mz
Определим неизвестные реакции расчётной балки R1 и R2 на основании двух уравнений равновесия (10.1) и (10.2):
![]() , (10.1)
, (10.1)
![]() , (10.2)
, (10.2)
Из уравнения (10.1) составим уравнение моментов относительно точки 1. Получим:
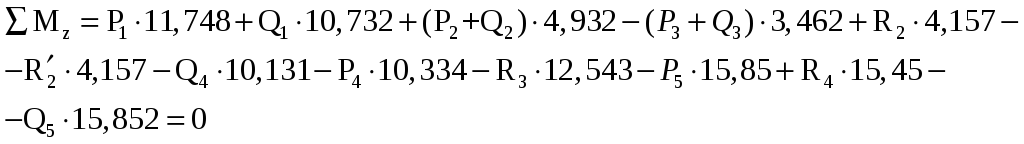
Массовые силы от распределенной нагрузки будут равны:
![]()
![]()
![]()
![]()
![]()
Подставим значения известных нам сил:

Преобразуем:
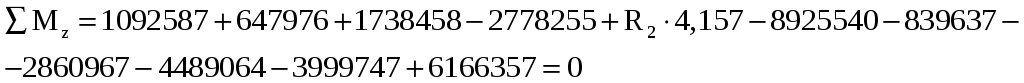
Откуда выражаем неизвестную реакцию R2:
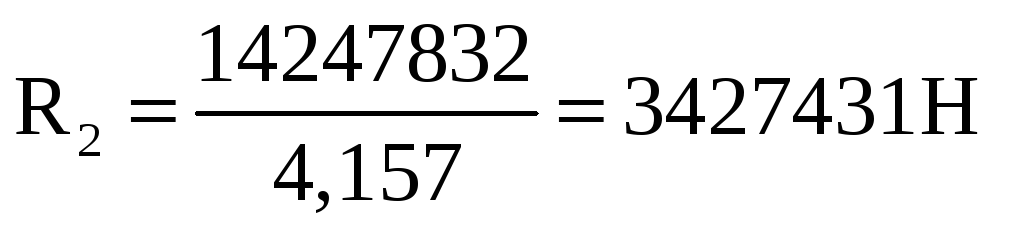
Из уравнения (10.2) находим неизвестную реакцию R1:
![]()
Подставим значения:

Отсюда находим:
![]() .
.
Зная все реакции и силы, мы можем приступить непосредственно к построению эпюр. Для этого делаем разбивку нашей балки на 11 участков, в соответствии с приложенными нагрузками, и для каждого из участков находим:
Участок I
П![]() роизведем
расчет эпюр перерезывающих сил Qy.
Расчет начинаем вести от начала координат
(нос самолета) путем последовательного
приращения сил в точках приложения
сосредоточенных сил или изломов
распределенных нагрузок. При этом будем
иметь 12 участков (приложение Г):
роизведем
расчет эпюр перерезывающих сил Qy.
Расчет начинаем вести от начала координат
(нос самолета) путем последовательного
приращения сил в точках приложения
сосредоточенных сил или изломов
распределенных нагрузок. При этом будем
иметь 12 участков (приложение Г):
Участок I
![]()
![]()
Участок II
![]()
![]()
![]()
![]()
У![]() часток
III
часток
III
У![]() часток
IV
часток
IV
![]()
![]()
![]()
![]()
У![]() часток
V
часток
V
![]()
![]()
![]()
У![]() часток
VI
часток
VI
![]()
![]()
![]()
У![]() часток
VII
часток
VII
![]()
![]()
У![]() часток
VIII
часток
VIII
![]()
У![]()
![]() часток
IX
часток
IX
![]()
![]()
У![]()
![]() часток
X
часток
X
![]()
![]()
![]()
У![]() часток
XI
часток
XI
Расчет изгибающих моментов будем вести в два этапа. На первом этапе идем от начала координат шесть участков. Далее проходим пять участков с конца и соединяем эпюру Mz (данный подход значительно сокращает объем расчетов).
Э![]() тап
1
тап
1
Участок I
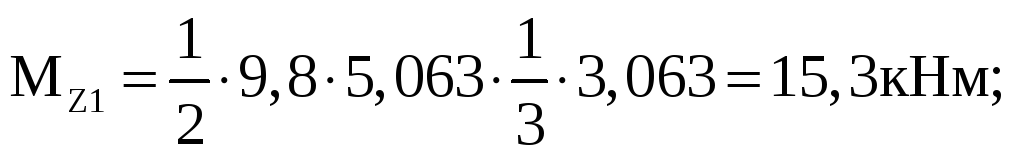
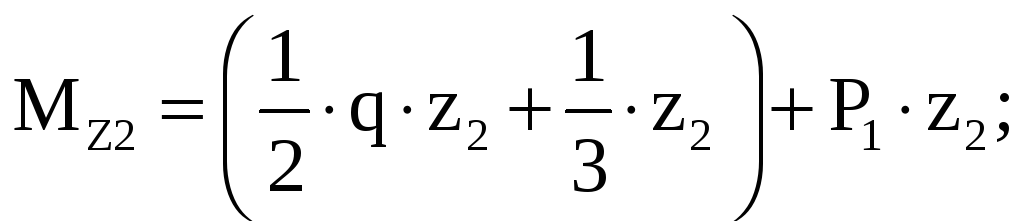
участок II
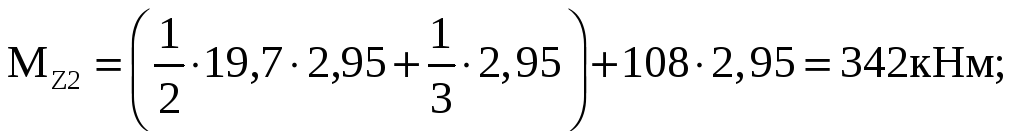
![]()
участок III
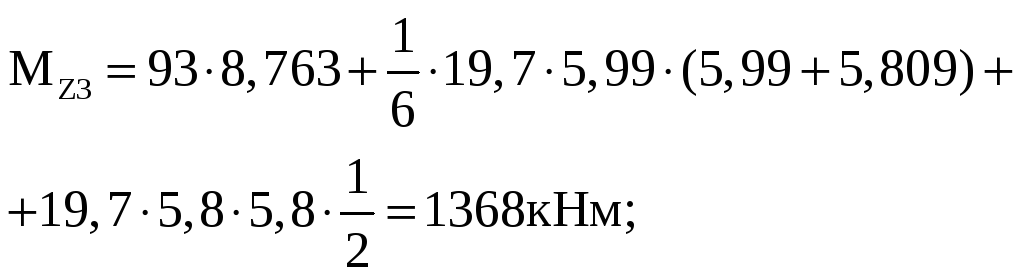
![]()
участок IV
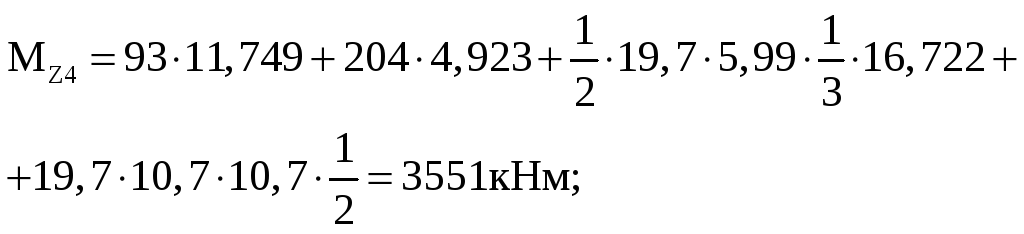
у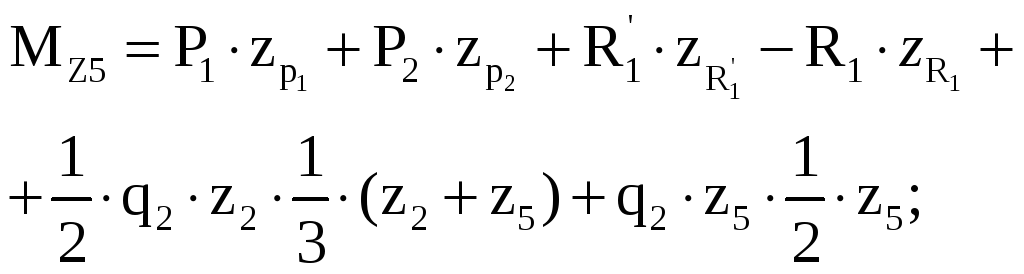 часток
V
часток
V
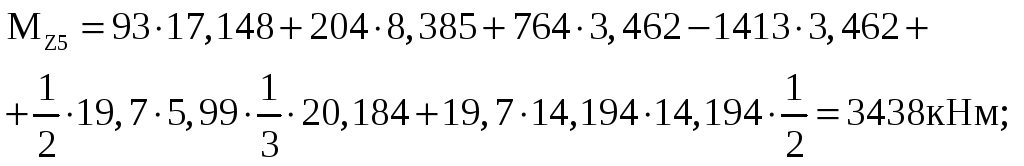
у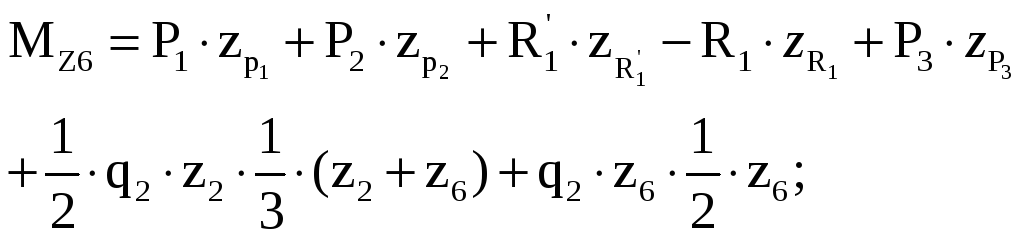 часток
VI
часток
VI

Э![]() тап
2
тап
2
участок XI
![]()
у![]() часток
X
часток
X
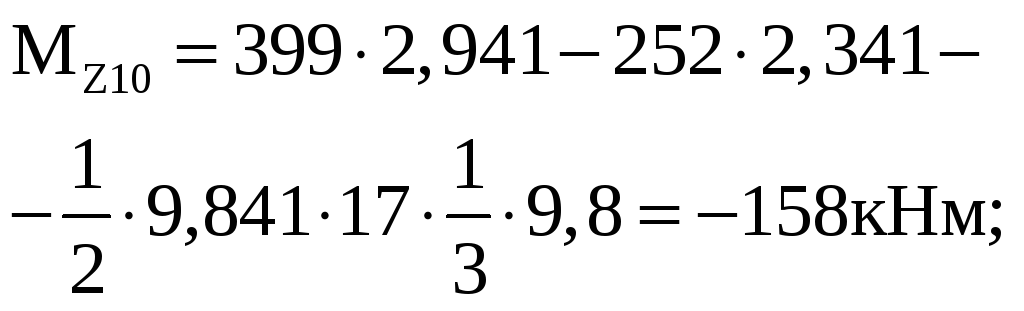
![]()
участок IX
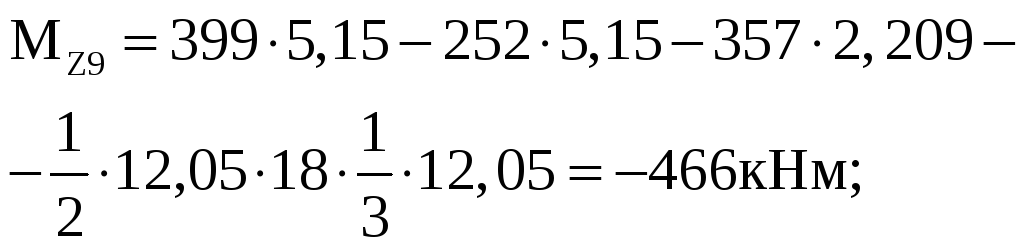
У![]() часток
VIII
часток
VIII
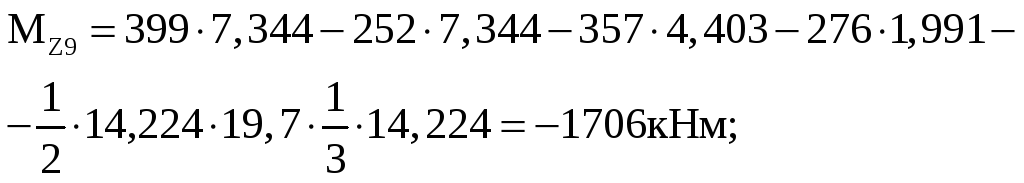
У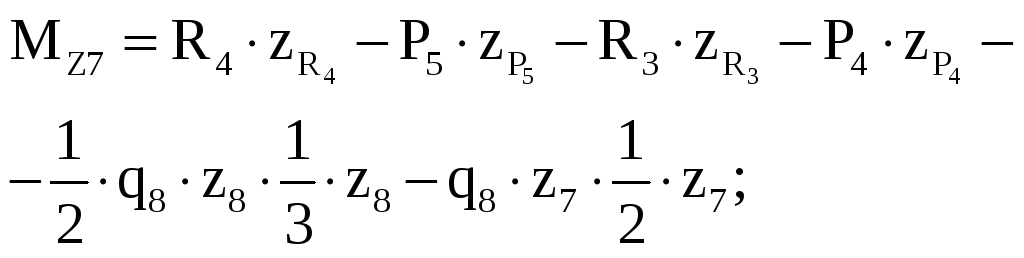 часток
VII
часток
VII

На рисунке 15 показаны эпюры перерезывающих сил Qу и изгибающих моментов Mz.
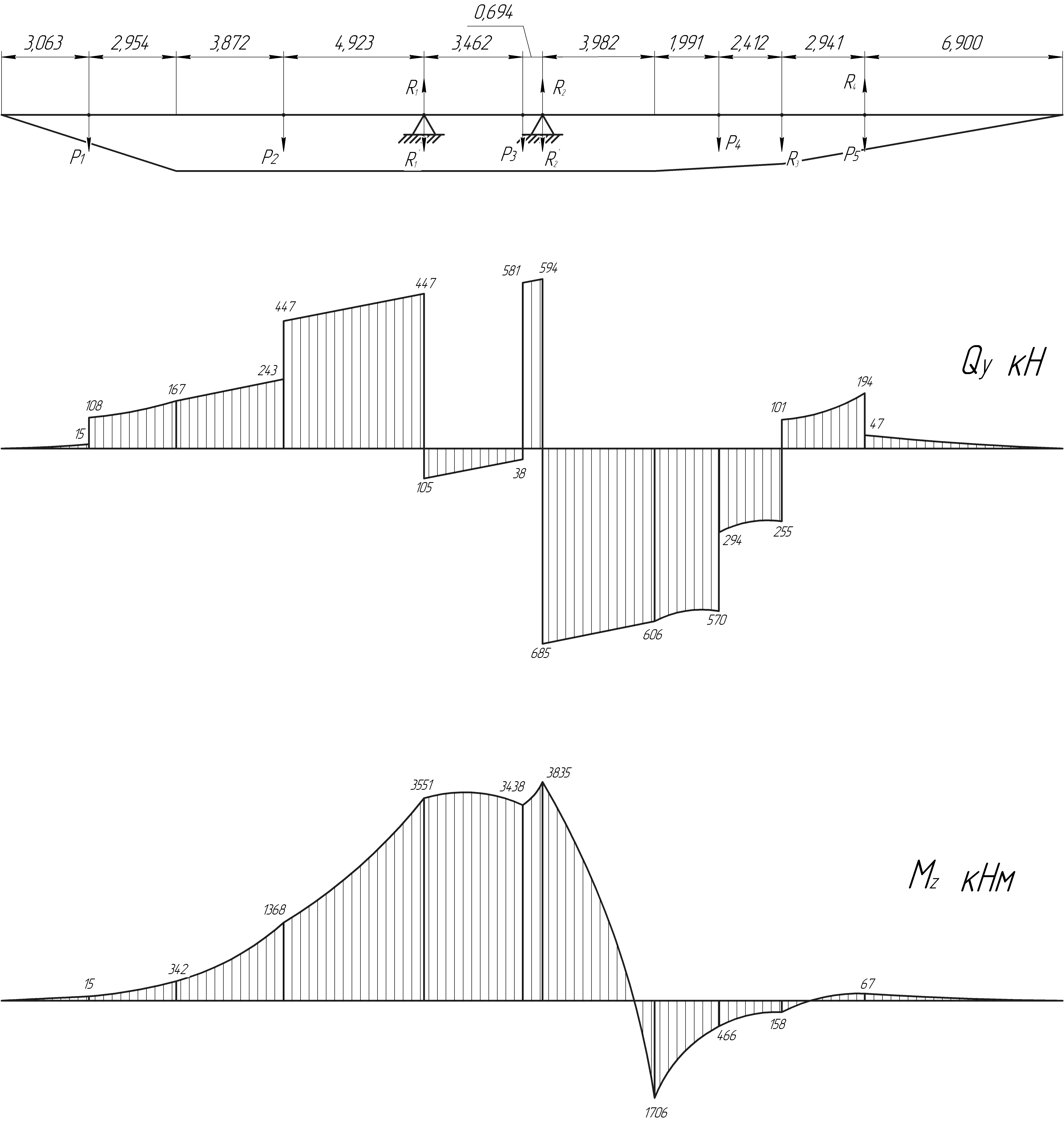
Рисунок 15 – Эпюры Qу и Mz.
11 Предварительное проектирование силового набора фюзеляжа
Силовой набор балочно-стрингерного фюзеляжа (монокок).
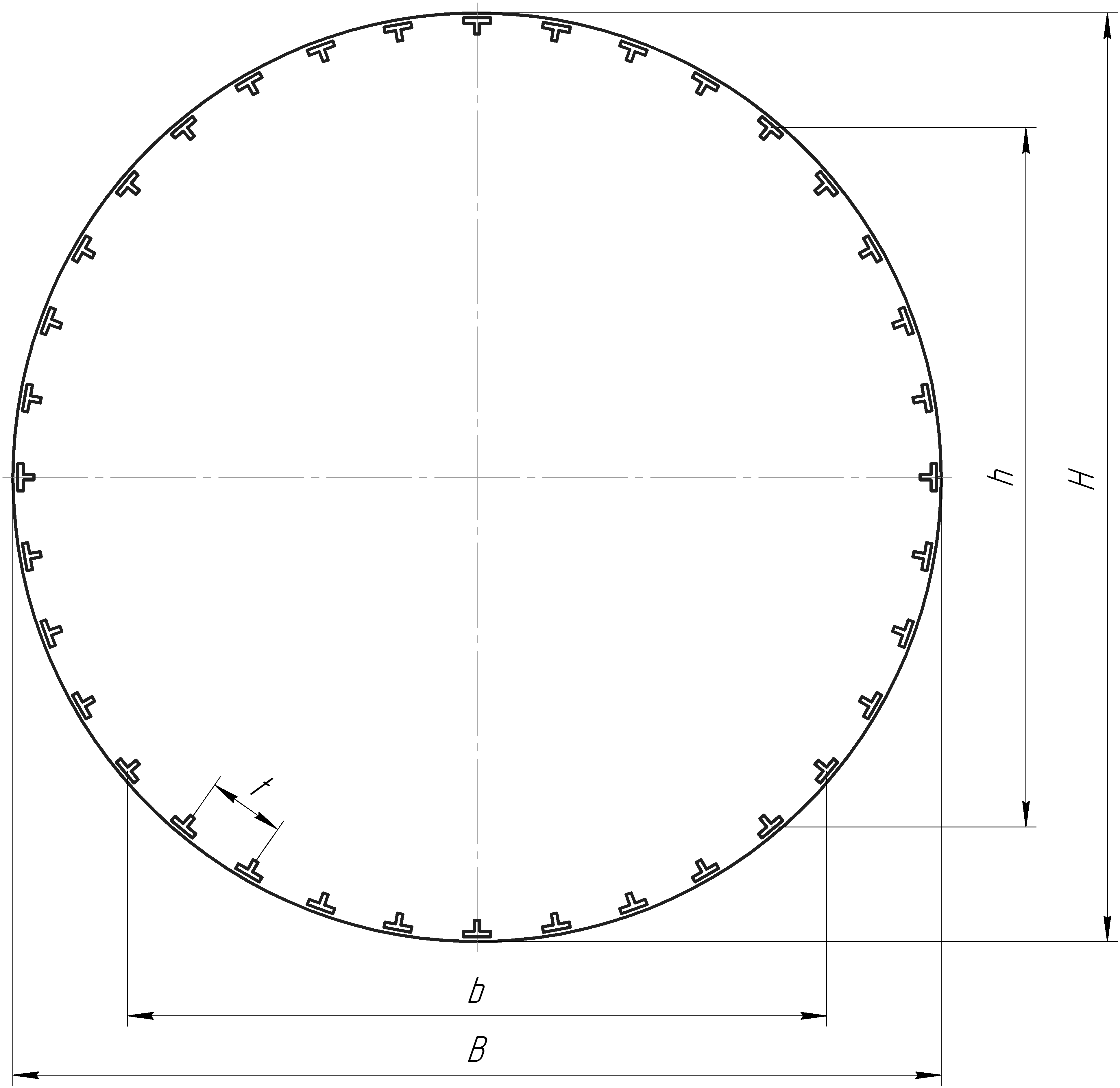
Рисунок 16 – Поперечное сечение балочно-стрингерного фюзеляжа
Для силового набора балочно-стрингерного фюзеляжа примем следующие параметры и соотношения (рисунок 16)
Н – высота сечения фюзеляжа, мм;
h=0,7H – высота боковины фюзеляжа, мм;
В – ширина сечения фюзеляжа, мм;
b=0,7B – ширина свода фюзеляжа, мм;
fстр – площадь стрингера, мм2.
В нашем случае
Н=2900 мм;
h=2030 мм;
b=2030 мм;
fстр=2000 мм2;
В=2900 мм.
Рассчитаем количество стрингеров n:
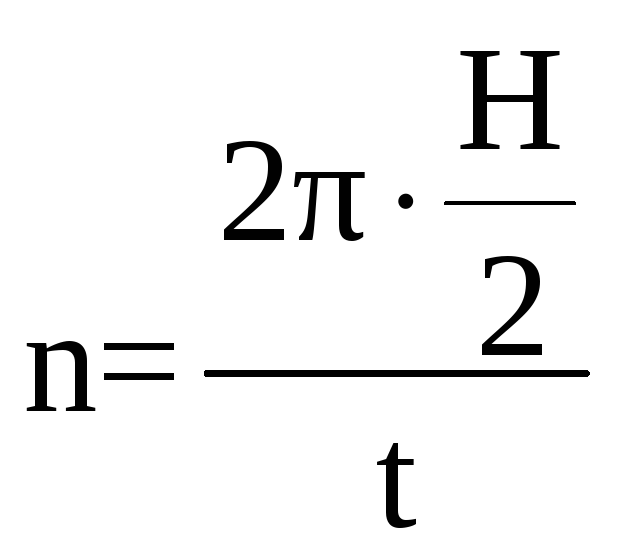 (11.1)
(11.1)
где t – шаг стрингеров, мм.
Примем шаг стрингеров равным t=230 мм, тогда количество стрингеров
![]()
Рассчитаем геометрические размеры стрингера (рисунок 17):
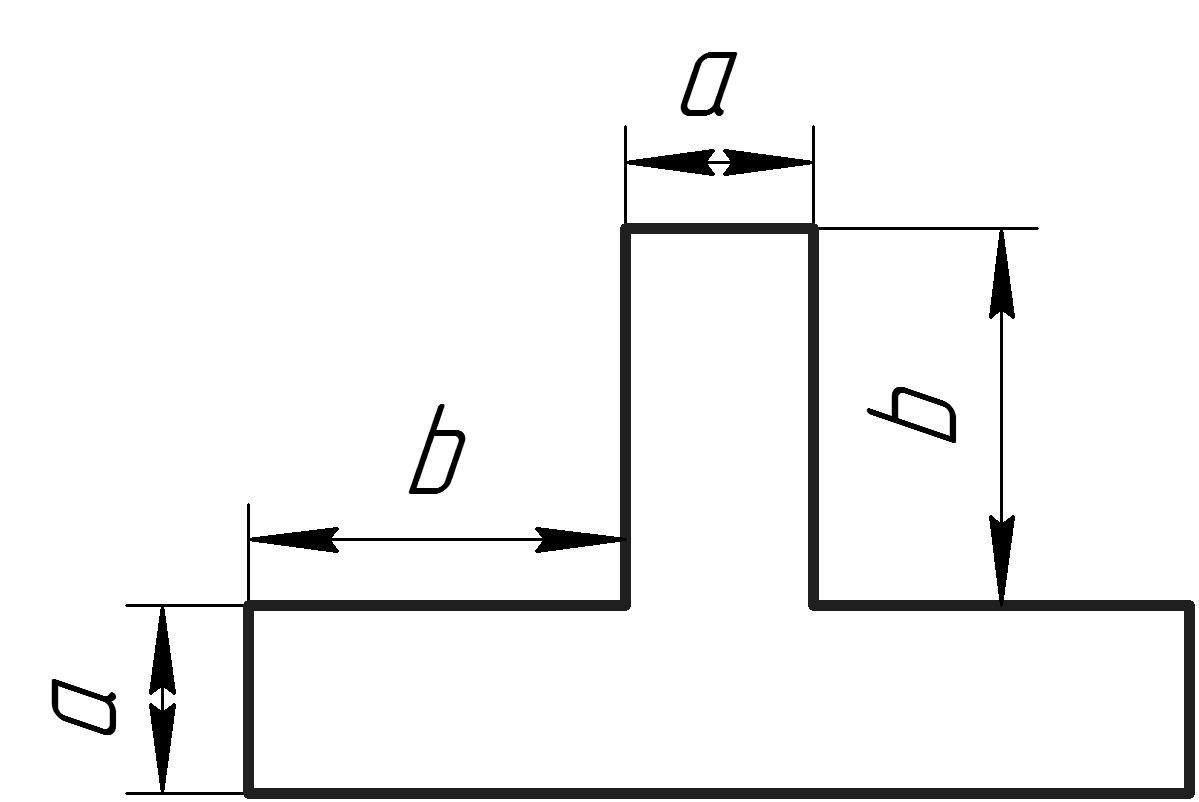
Рисунок 17 – Сечение стрингера
Площадь стрингера:
![]() ;
;
![]() ;
;
![]() .
.
Примем, что:
![]()
Тогда:
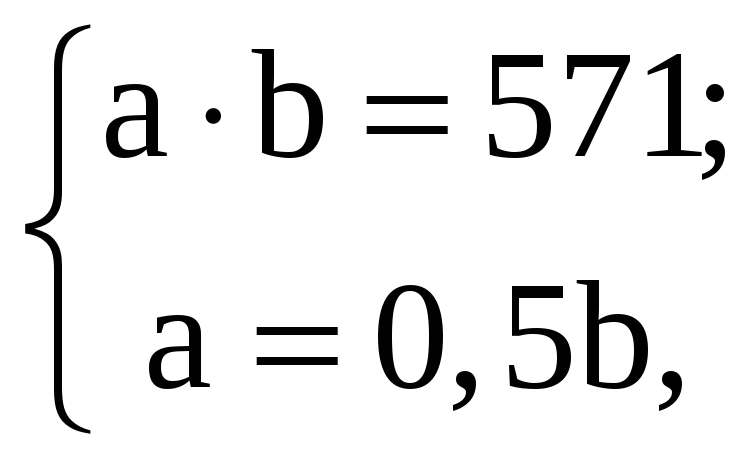
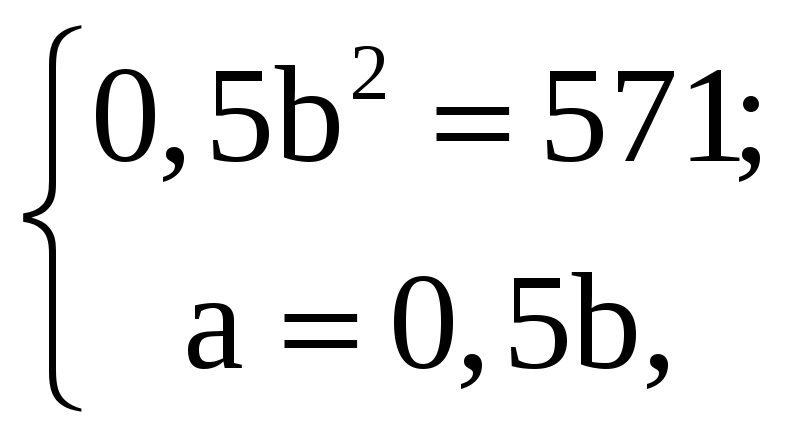
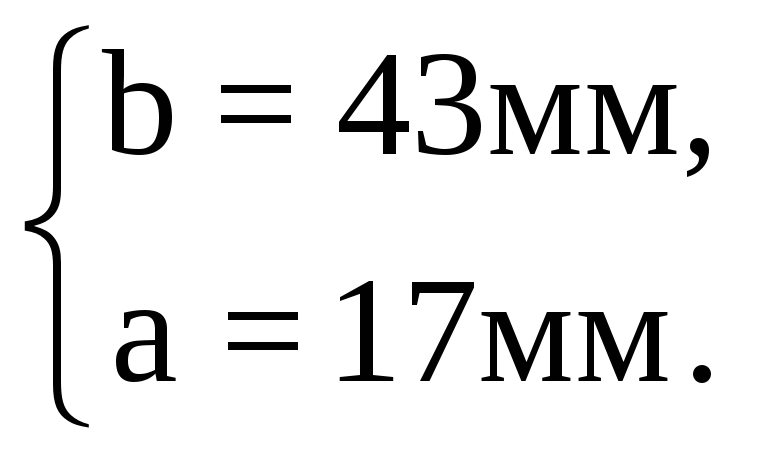
С учетом полученных
геометрических размеров площадь
стрингера
![]() .
.
12 Проектировочный расчет трех сечений фюзеляжа
Определение толщины
обшивки фюзеляжа
![]()
Толщина обшивки фюзеляжа может быть определена по формуле:
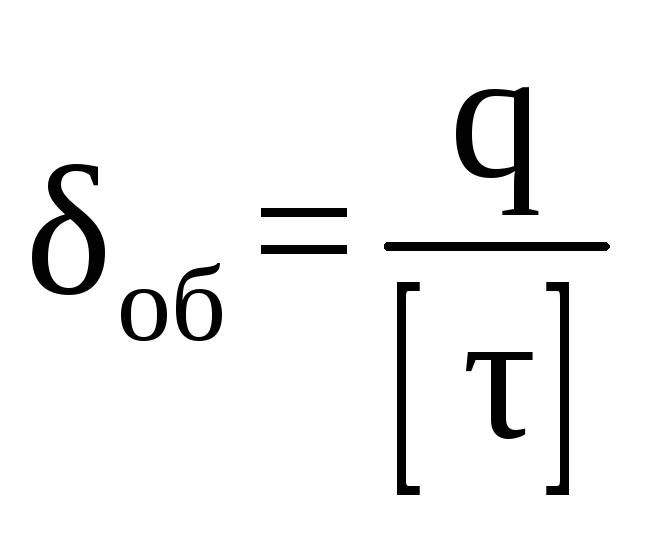 , (12.1)
, (12.1)
![]() . (12.2)
. (12.2)
Касательное, распределенное по обшивке усилие q выбираем как наибольшее из величин q1 и q2.
q1 – касательное усилие от действия вертикальной поперечной силы, Н/м;
q2 – касательное усилие, возникающее от боковой силы Pво, на ВО, Н/м.
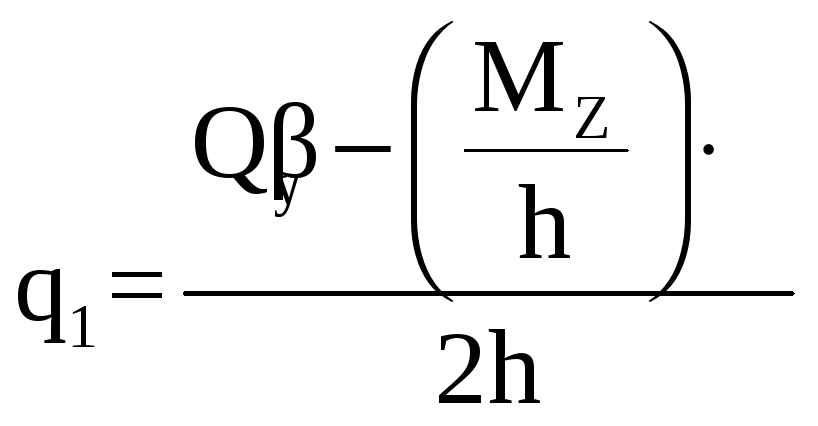 , (12.3)
, (12.3)
где
![]() – перерезывающая сила, H;
– перерезывающая сила, H;
![]() – изгибающий
момент, Нм;
– изгибающий
момент, Нм;
h – высота боковины фюзеляжа, м;
β – угол между лонжеронами при виде на фюзеляж сбоку, рад.
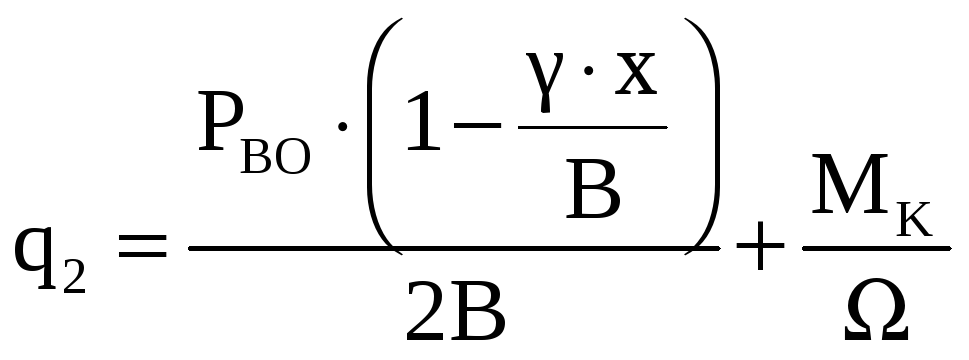 , (12.4)
, (12.4)
![]() , (12.5)
, (12.5)
где
![]() – площадь сечения фюзеляжа, м2;
– площадь сечения фюзеляжа, м2;
В – ширина сечения фюзеляжа, м;
γ – угол между лонжеронами при виде на фюзеляж сверху, рад;
x – расстояние по вертикали от вектора силы PВО от рассматриваемого
сечения, м.
1) Рассчитаем
толщину обшивки для первого сечения
(![]() кН/м,
кН/м,
![]() кН):
кН):
Т.к β=0, получим:
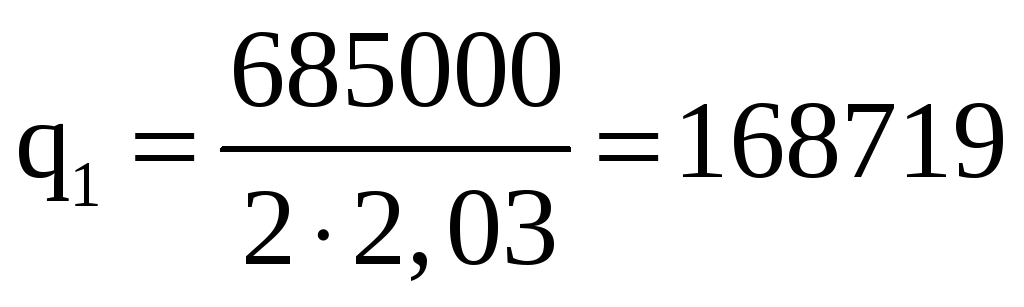 Н/м.
Н/м.
Т.к γ=0, получим:
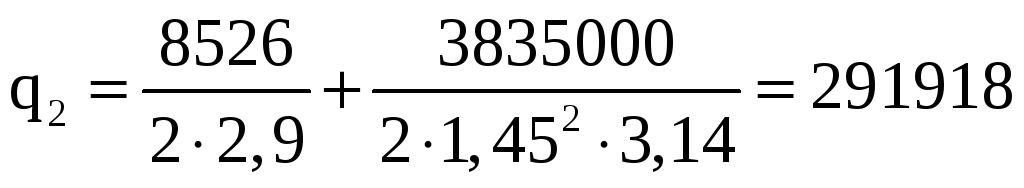 Н/м.
Н/м.
Толщина обшивки с учетом того, что q1>q2
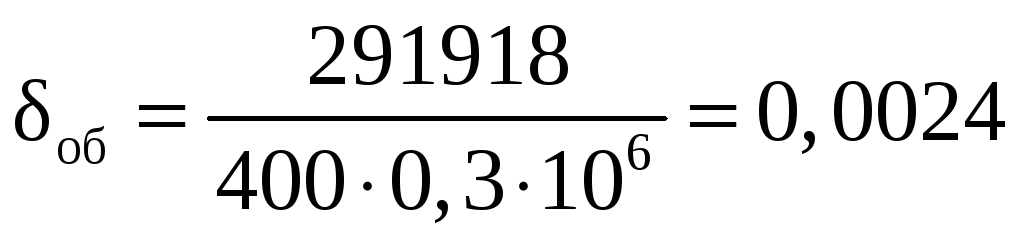 м.
м.
2) Рассчитаем
толщину обшивки для второго сечения
(![]() кН/м,
кН/м,
![]() кН):
кН):
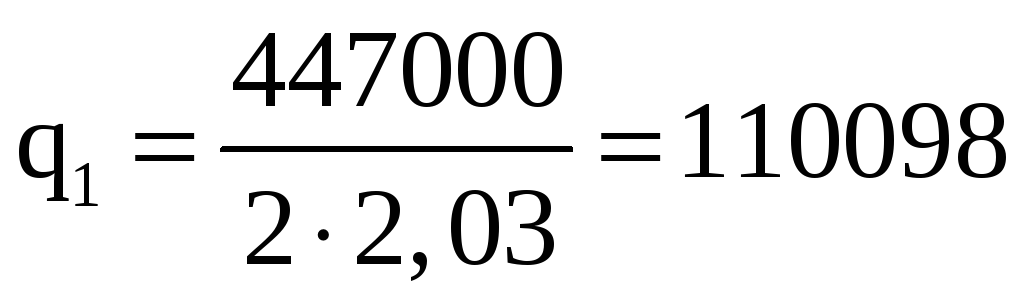 Н/м,
Н/м,
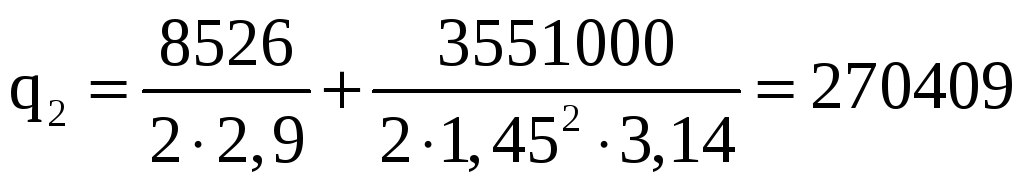 Н/м.
Н/м.
Толщина обшивки с учетом того, что q1>q2
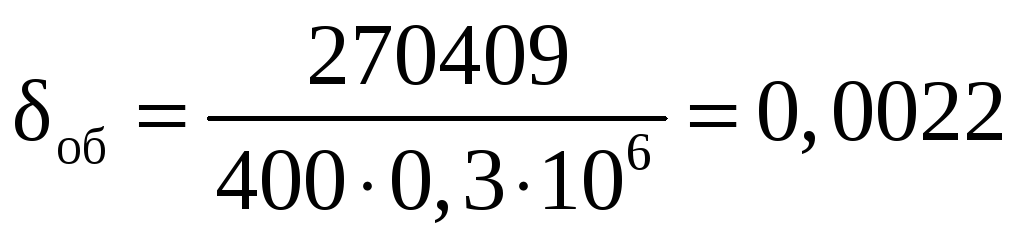 м.
м.
3) Рассчитаем
толщину обшивки для третьего сечения
(![]() кН/м,
кН/м,
![]() кН):
кН):
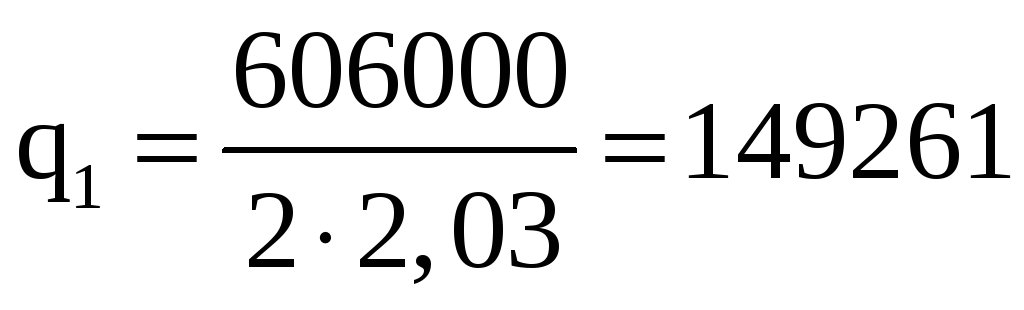 Н/м,
Н/м,
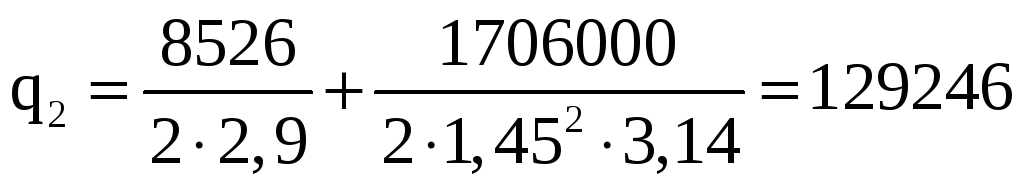 Н/м.
Н/м.
Толщина обшивки с учетом того, что q1<q2
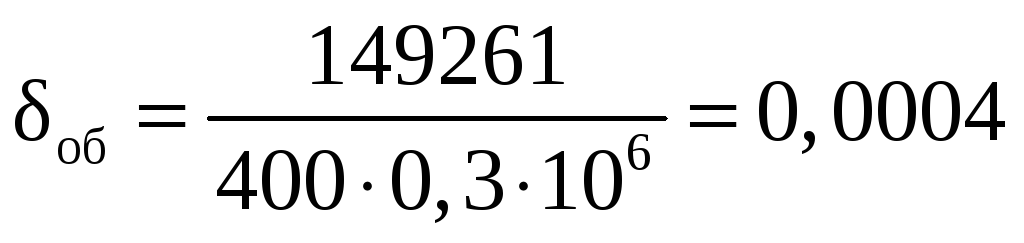 м.
м.
13 Определение напряжений в наиболее нагруженном сечении фюзеляжа
Определение максимальных напряжений в сечении фюзеляжа может быть рассчитано по формуле:
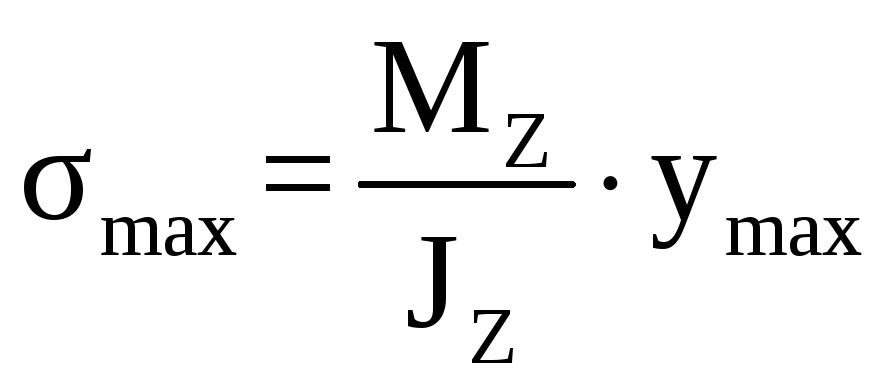 (13.1)
(13.1)
где
![]() – максимальный изгибающий момент,
действующий на фюзеляж. Его
– максимальный изгибающий момент,
действующий на фюзеляж. Его
величину возьмем
с эпюры моментов
![]() ;
;
![]() – максимальное
расстояние по вертикали от центра
тяжести сечения
– максимальное
расстояние по вертикали от центра
тяжести сечения
фюзеляжа до крайнего элемента этого сечения;
![]() – момент инерции
сечения фюзеляжа относительно оси 0Z,
– момент инерции
сечения фюзеляжа относительно оси 0Z,
проходящей через центр тяжести сечения фюзеляжа.
Таким образом,
задача расчета максимальных напряжений,
действующих в сечении фюзеляжа сводиться
к определению положения центра тяжести
сечения фюзеляжа
![]() и расчету момента инерции сечения
и расчету момента инерции сечения
![]() .
Т.к сечение фюзеляжа симметрично
относительно оси 0Z,
то необходимо определить только момент
инерции сечения
.
Т.к сечение фюзеляжа симметрично
относительно оси 0Z,
то необходимо определить только момент
инерции сечения
![]() .
.
14 Определение
момента инерции сечения фюзеляжа
![]() относительно оси 0Z,
проходящей через центр тяжести сечения
фюзеляжа
относительно оси 0Z,
проходящей через центр тяжести сечения
фюзеляжа
Момент инерции
сечения фюзеляжа
![]() определится по формуле:
определится по формуле:
![]() , (14.1)
, (14.1)
где
![]() ,
,
![]() ,
,
![]() – собственные моменты инерции стрингеров
1, 2, …n;
– собственные моменты инерции стрингеров
1, 2, …n;
![]() ,
,
![]() ,
,
![]() – координаты центров тяжести элементов
1, 2, …n
– координаты центров тяжести элементов
1, 2, …n
сечения фюзеляжа относительно центра тяжести всего сечения фюзеляжа.
14.1 Определение собственных моментов инерции сечений
Примем следующие обозначения (рисунок 18):
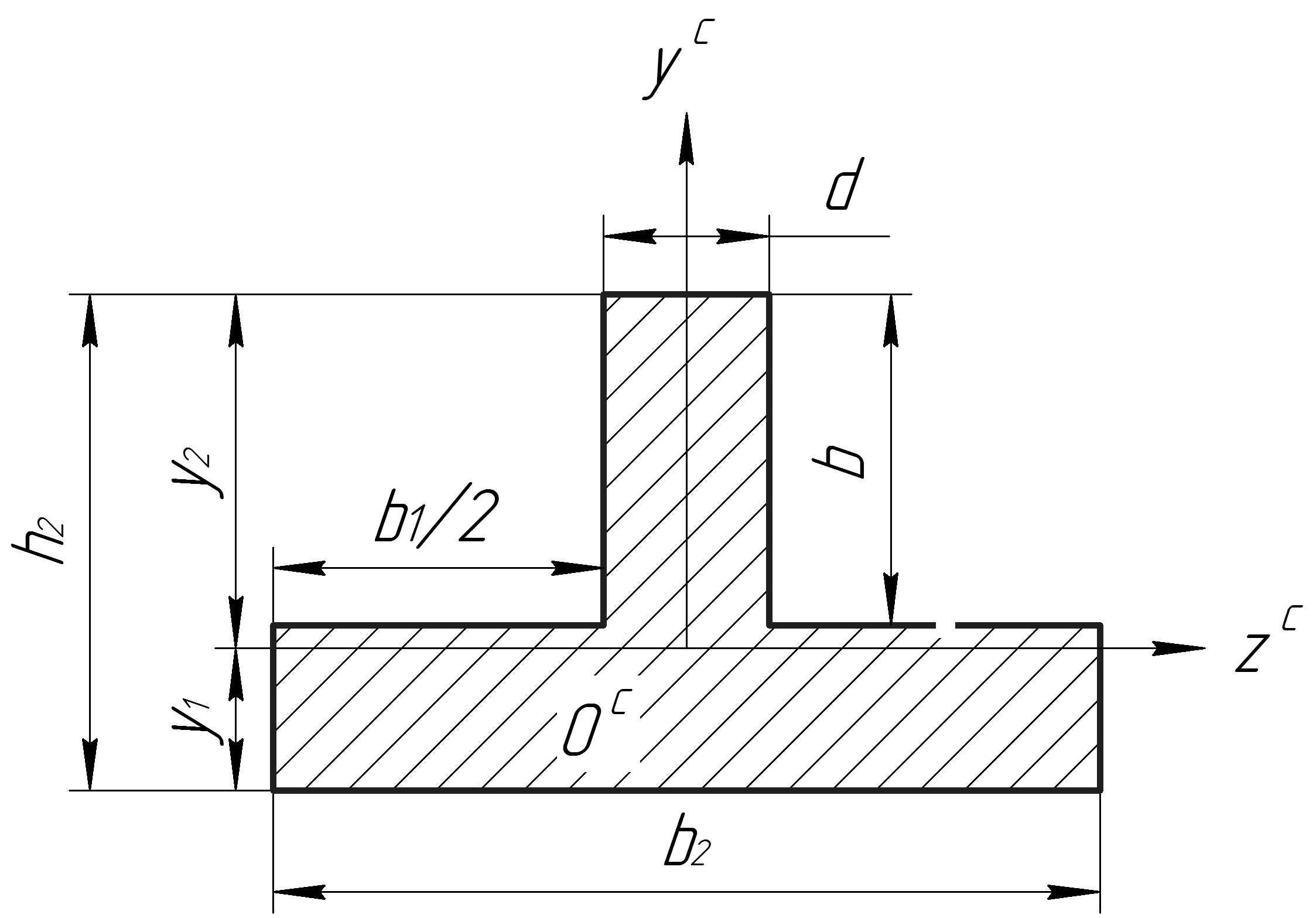
Рисунок 18 – Определение собственного момента инерции
Приняты следующие обозначения:
b1 = b2 – d
b1 = 85 – 17 = 68 мм
h1 = y1 – d
![]()
![]() мм
мм
Координата Ц.Т тавра y1 относительно его основания:
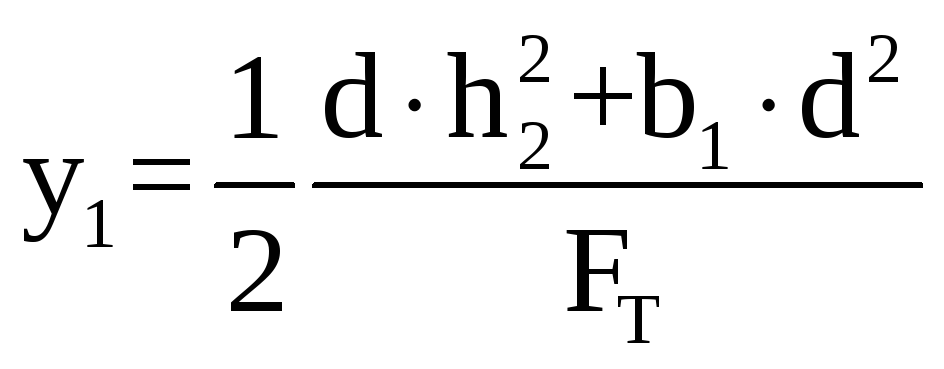 , (14.2)
, (14.2)
где
![]() – площадь сечения тавра, мм2.
– площадь сечения тавра, мм2.
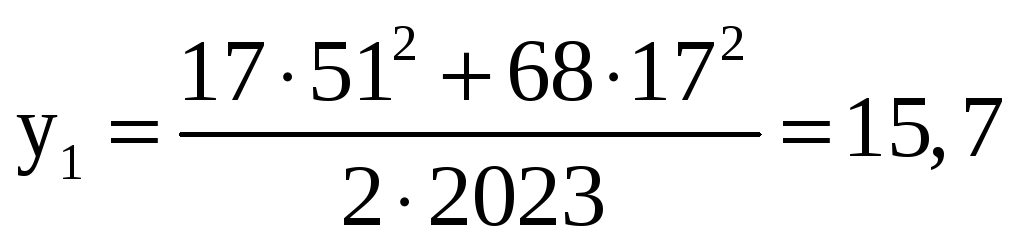 мм.
мм.
Моменты инерции
тавра относительно осей 0сzc
и 0сyc,
проходящих через Ц.Т –
![]() и
и
![]() :
:
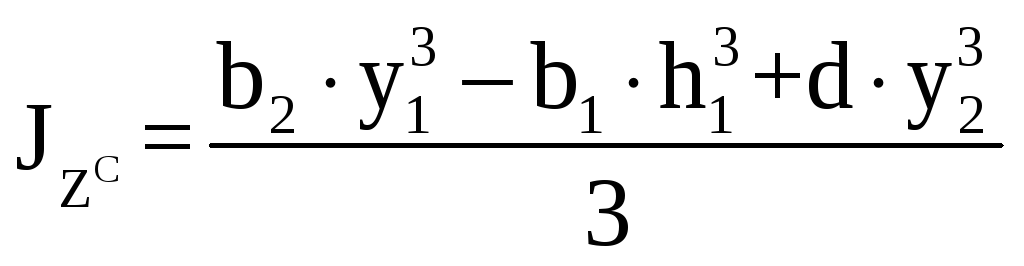 , (14.3)
, (14.3)
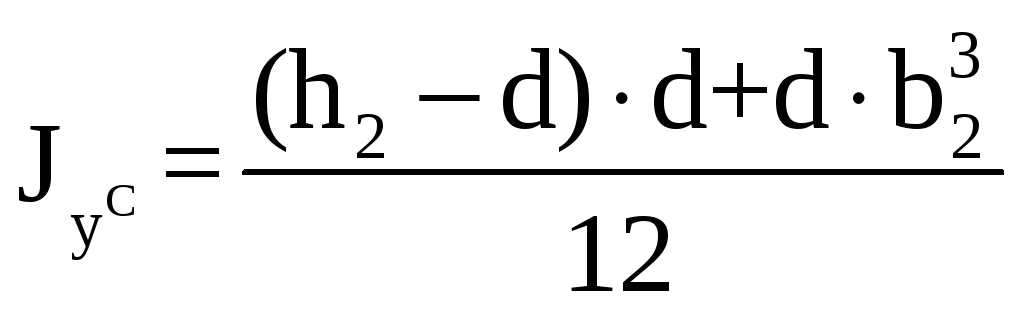 , (14.4)
, (14.4)
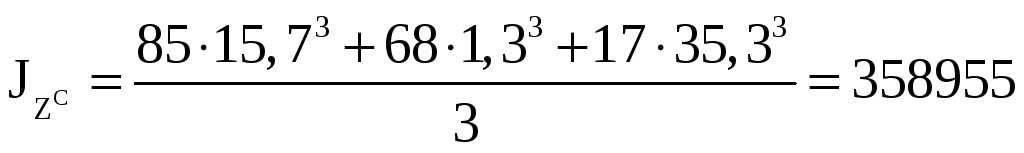 мм4
мм4
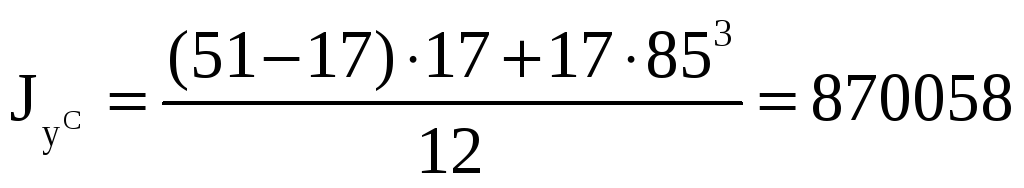 мм4
мм4
Минимальный момент сопротивления сечения тавра относительно 0сZc:
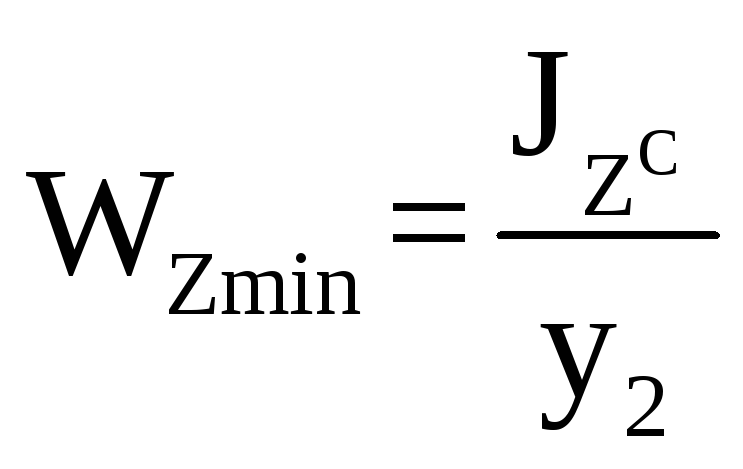 , (14.5)
, (14.5)
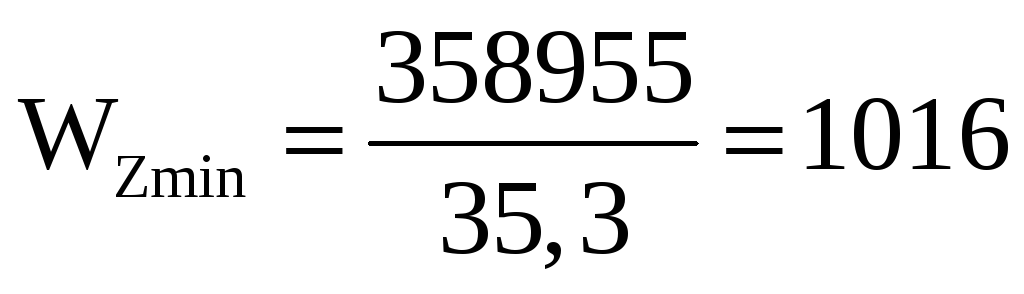 мм3
мм3
Определим моменты инерции сечений профилей, относительно произвольных осей, проведенных через Ц.Т сечений по формуле:
![]() (14.6)
(14.6)
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() .
.
Рассчитаем момент
инерции сечения фюзеляжа
![]() по формуле (14.1):
по формуле (14.1):

Максимальное напряжение в сечении фюзеляжа: