5 Нагрузки, действующие на фюзеляж

Фюзеляж данного самолёта условно разбит на 5 отсеков. Найдём суммарную вертикальную силу P_i в каждом отсеке.

В первом отсеке длиной 6127 мм действует суммарная вертикальная сила, P₁ которая находится по формуле:

, (5.1)

где n_р – расчетная перегрузка.

, (5.2)

где f – коэффициент безопасности;

n_э – эксплуатационная перегрузка.

Найдем расчетную перегрузку:

Тогда суммарная вертикальная сила P₁ будет равна:

.

Во втором отсеке длиной 7525 мм действует суммарная вертикальная сила P₂, которая находится по формуле:

, (5.3)

Определяем суммарную вертикальную силу P₂:

.

В третьем отсеке длиной 9245 мм действует суммарная вертикальная сила P₃, которая находится по формуле:

, (5.4)

Определяем суммарную вертикальную силу P₃:

.

В четвёртом отсеке длиной 4500 мм действует суммарная вертикальная сила P₄, которая находится по формуле:

, (5.5)

Находим суммарную вертикальную силу P₄:

.

В пятом отсеке длиной 5788 мм действует суммарная вертикальная сила P₅, которая находится по формуле:

, (5.6)

Находим суммарную вертикальную силу P₅:

.

Нагрузки, действующие на фюзеляж, показаны на рисунке 9.

Рисунок 9 – Нагрузки, действующие на фюзеляж

6 Определение реакций, действующих на фюзеляж от крыла

Подъёмная сила крыла определяется по формуле:

, (6.1)

.

Суммарный вес крыла равен:

, (6.2)

где G_кр – вес конструкции крыла, кг;

G_т – вес топлива, располагаемого в крыле, кг;

G_оснст – вес основных стоек шасси, расположенных в крыле, кг;

G_снаркр – вес снаряжения крыла, кг.

Вес конструкции крыла G_кр =8700 кг, масса топлива расположенного в крыле G_т =15844 кг, вес основных стоек шасси G_оснст =2610 кг, вес снаряжения крыла примем 5% от веса конструкции крыла G_снаркр =0,0058700=435 кг.

Отсюда получим:

.

Расчётная нагрузка от суммарного веса крыла:

, (6.3)

Получим:

.

Суммарная вертикальная сила , действующая на крыло, определяется по формуле:

, (6.4)

.

Дополнительный момент определяется по формуле:

, (6.5)

.

Определим реакции и , действующие на узлы крепления крыла к фюзеляжу (рисунок 10). Для этого составим два уравнения равновесия:

1 – центр давления; 2 – центр тяжести

Рисунок 10 – Определение реакций крыла, действующих на фюзеляж

(6.6)

Отсюда находим:

, (6.7)

Откуда:

, (6.8)

.

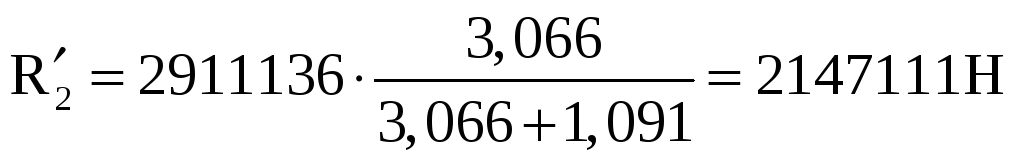, (6.9)

.

Делаем проверку по формуле:

, (6.10)

,

Реакции и найдены верно.

7 Определение реакций, действующих на фюзеляж от горизонтального и вертикального оперения

Подъёмная сила горизонтального оперения находится по формуле (7.1):

, (7.1)

Площадь горизонтального оперения , .

Суммарная вертикальная сила , действующая на горизонтальное оперение, находится по формуле (7.2):

, (7.2)

.

Определим нагрузки, действующие от ВО в вертикальной плоскости на фюзеляж:

В точке 5 на фюзеляж от вертикального оперения действует суммарная сила (в вертикальной плоскости) , равная:

.

На рисунке 11 показана схема нагружения хвостовой части фюзеляжа в вертикальной плоскости.

Рисунок 11 – Двухопорная балка

Определим суммарные нагрузки, действующие на фюзеляж от оперения (при помощи двух уравнений равновесия):

При перенесении силы из точки 6 в точку 5, возникает дополнительный момент М_ГО, равный:

, (7.3)

Размеры с₁, d₁ и b₁ показаны на рисунке12, отсюда .

В результате, в точке 5 на фюзеляж, вертикальной плоскости, от ГО и ВО будет действовать суммарная сила , и изгибающий момент М_ГО, причем:

(9.4)

,

,

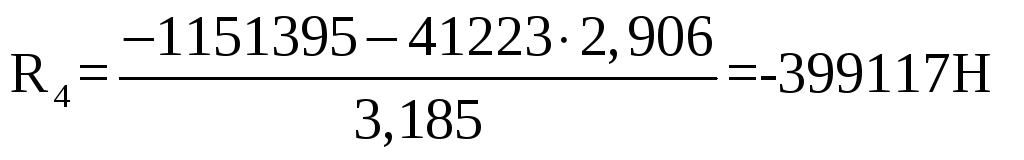
Из уравнений следует, что сила R₄ направлена вверх.

Рисунок 12 – Хвостовая часть фюзеляжа

8 Определение распределенных массовых сил от веса конструкции фюзеляжа

Распределенные массовые силы от веса конструкции фюзеляжа q_Ф находится по формуле (8.1):

, (8.1)

где H_iФ – текущая высота фюзеляжа, м;

S_бок – площадь боковой проекции фюзеляжа на плоскость XOY, м².

Боковая площадь была вычислена при помощи программы Компас 3D V12 и составляет .

Размеры H_1Ф=0 м; H_2Ф=2,9 м; H_3Ф=2,9 м; H_4Ф=2,9 м; H_5Ф=2,52 м взяты с чертежа и показаны в соответствии с рисунком 13.

;

;

;

.

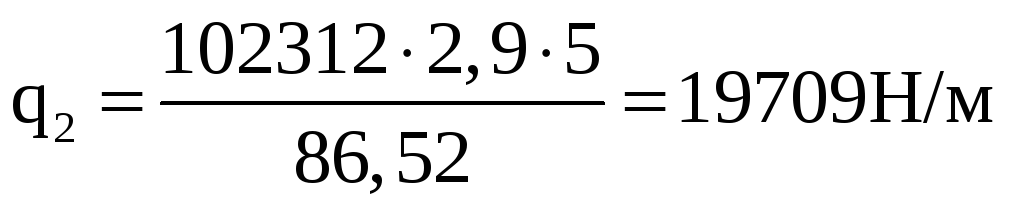Отсюда видно, что массовые силы от веса конструкции в отсеках 2 – 4 одинаковы.

Рисунок 13 – Эпюра распределённых сил

9 Расчет крутящего момента M_КР

Крутящий момент M_КР находится по формуле (9.1):

, (9.1)

где h_ВО – плечо силы до строительной горизонтали фюзеляжа;

– боковая сила (направлена параллельно оси OZ), действующая на ВО.

Сила рассчитывается по формуле (9.2):

, (9.2)

где – коэффициент боковой силы при отклонении руля направления;

– расчетная перегрузка в горизонтальной плоскости.

Перегрузка рассчитывается по формуле (9.3):

, (9.3)

где – эксплуатационная перегрузка в плоскости X0Z;

f – коэффициент безопасности.

Примем эксплуатационную перегрузку , коэффициент безопасности , коэффициент боковой силы , отсюда находим:

, ,

.

Общий крутящий момент M_КР, действующий на фюзеляж, необходимо распределить на силовые шпангоуты крепления киля к фюзеляжу, плоскости которых проходят через точки 3 и 4 рисунок 14.

Распределение момента M_КР рассчитывается по формуле (9.4) и (9.5):

, (9.4)

, (9.5)

Из данных уравнений:

, ,

Отсюда находим:

,

,.

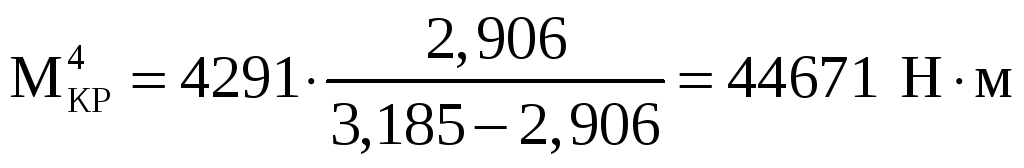Эпюра крутящих моментов, действующих на фюзеляж, изображена на рисунке 14.

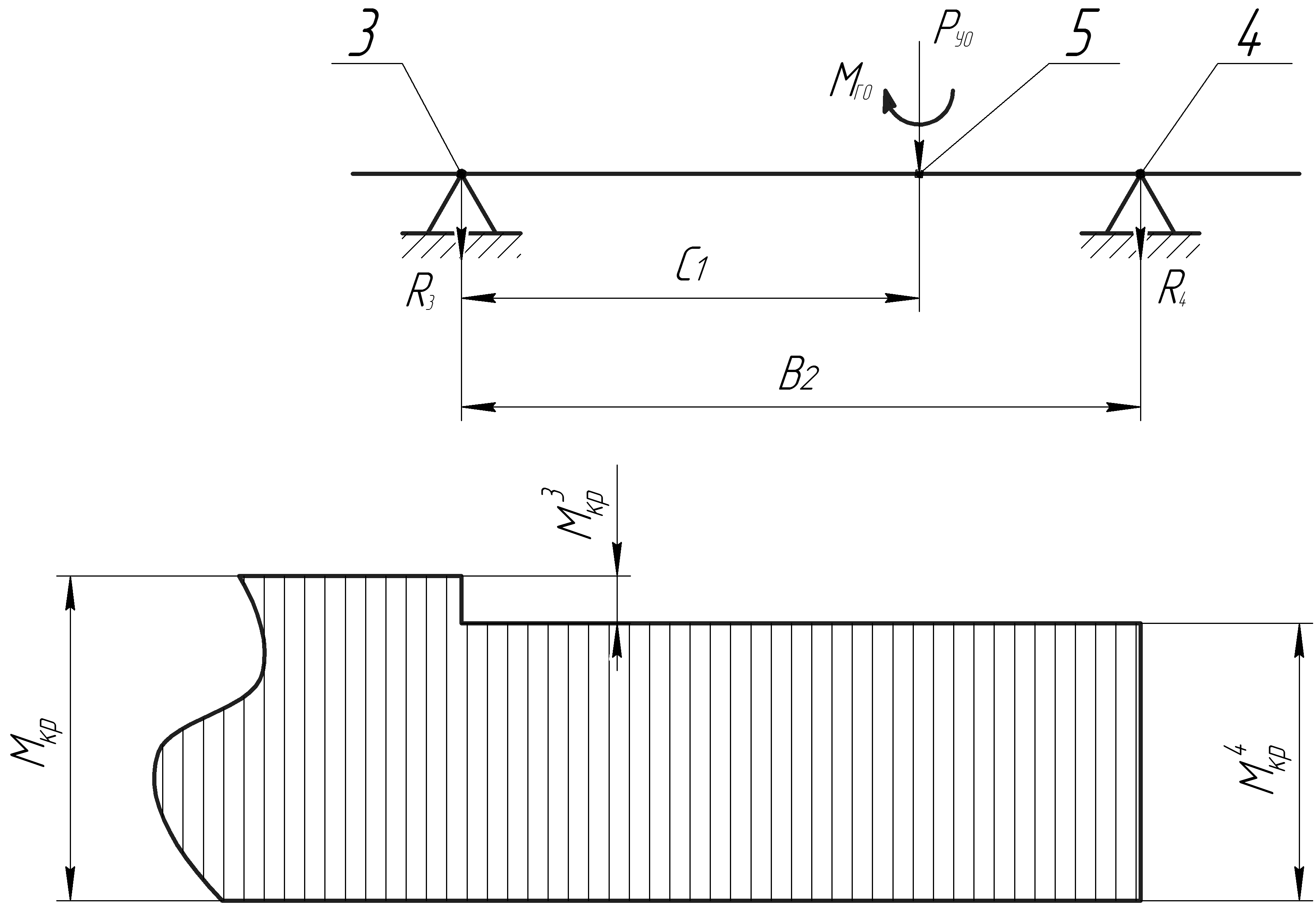
Рисунок 14 – Схема нагружения хвостовой части фюзеляжа от ВО.