
- •1. Основные понятия теории вероятностей
- •1.1. Распределения вероятностей
- •Непрерывной случайной величины х
- •1.1.2. Теоретические распределения вероятностей
- •Распределения Пирсона
- •1.3. Моделирование реализации случайных процессов
- •2 Экспериментальные факторные математические модели
- •2.1. Особенности экспериментальных факторных моделей
- •2.1.1. Основные принципы планирования эксперимента
- •2.1.2 План эксперимента
- •2.2. Регрессионный анализ
- •2.2.1. Оценка параметров регрессионной модели
- •2.3. Корреляционный анализ
- •2.3.1. Основные понятия
- •3.2.1. Точечные оценки параметров
- •2.3.3. Приемы вычисления выборочных
- •2.3.4. Проверка значимости параметров связи
- •2.3.5. Интервальные оценки параметров связи
- •2.4. Трехмерная модель
- •2.4.1. Основные параметры модели
- •Условное распределение при заданном z
- •Условное распределение при заданном (х, у)
- •2.4.2. Оценивание и проверка значимости параметров
- •3. Методы многомерной классификации
- •3.1. Классификация без обучения. Кластерный анализ
- •3.1.1. Основные понятия
- •3.1.2. Расстояние между объектами и мера близости
- •Расстояние махаланобиса (общий вид)
- •Обычное евклидово расстояние
- •"Взвешенное" евклидово расстояние
- •Хеммингово расстояние
- •3.1.3. Расстояние между кластерами
- •3.1.4. Функционалы качества разбиения
- •3.1.5. Иерархические кластер-процедуры
- •3.2. Дискриминантный анализ
- •3.2.1. Методы классификации с обучением
- •3.2.2. Линейный дискриминантный анализ
- •3.2.3. Дискриминантный анализ при нормальном законе распределения показателей
3.2.3. Дискриминантный анализ при нормальном законе распределения показателей
Имеются две генеральные совокупности Х и У, имеющие трехмерный нормальный закон распределения с неизвестными, но равными ковариационными матрицами. Из них взяты обучающие выборки с объемами n1yX и n2yY.
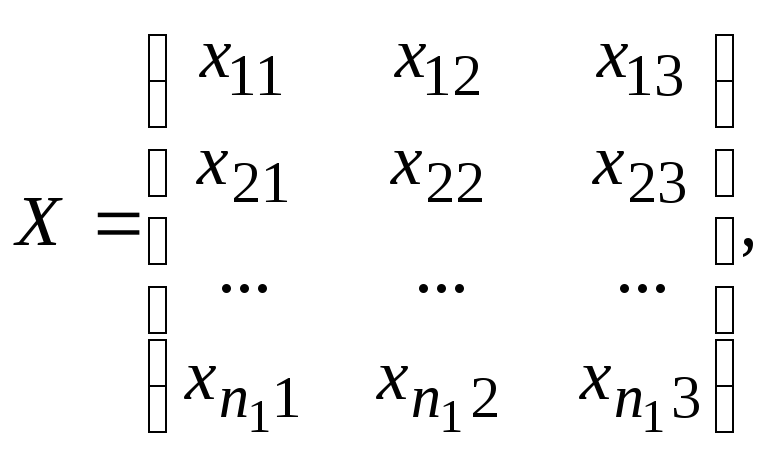 (157)
(157)
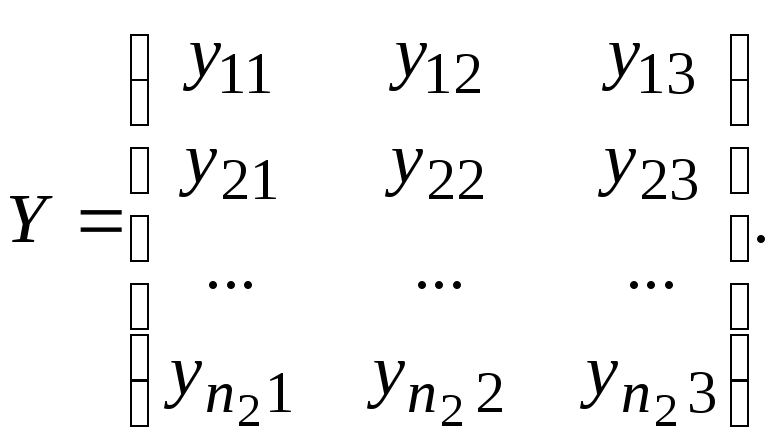 (158)
(158)
Целью дискриминантного анализа является отнесение нового наблюдения (строки матрицы Z) либо к X, либо к Y.
 (159)
(159)
Для решения задачи по обучающим выборкам определим векторы средних:
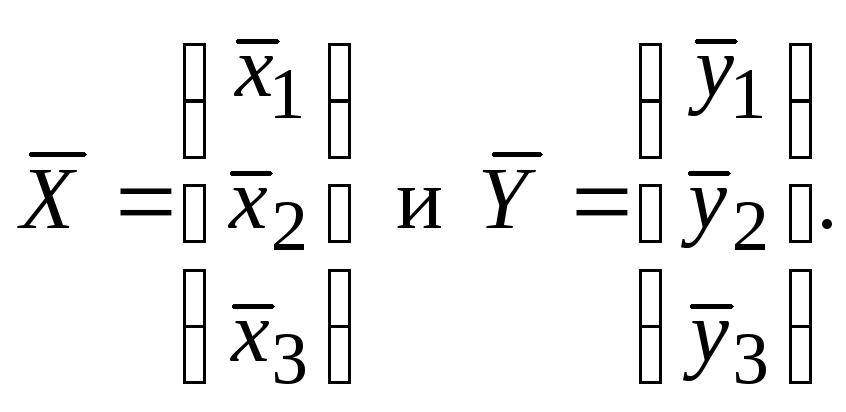
1. Определим оценки ковариационных матриц:
![]()
Найдем элемент матрицы Sх:
![]()
где
![]() и
и
![]() — средние
значения.
— средние
значения.
2. Рассчитаем несмещенную оценку суммарной ковариационной матрицы:
![]()
3.
Определим матрицу
![]() ,
обратную к
,
обратную к
![]()
4.
Вычислим вектор оценок коэффициентов
дискриминантной функции
![]()
5.
Рассчитаем оценки векторов значений
дискриминантной функции для матриц
исходных данных
![]()
![]() .
.
6. Вычислим средние значения оценок дискриминантной функции:
![]()
![]()
7.
Определим константу
![]()
Дискриминантную функцию для v-ого наблюдения, подлежащего дискриминации, получим, решив уравнение
![]()
Если
![]() ,
тоv-е
наблюдение надо отнести к совокупности
х,
если же
,
тоv-е
наблюдение надо отнести к совокупности
х,
если же
![]() ,
тоv
-е наблюдение следует отнести к
совокупности у.
,
тоv
-е наблюдение следует отнести к
совокупности у.
