2.4. Трехмерная модель

2.4.1. Основные параметры модели

Для изучения основных задач и особенностей корреляционного анализа удобно рассматривать генеральную совокупность трех признаков х, у и z.

Трехмерная непрерывная случайная величина (х, у, z) называется нормально распределенной, если плотность совместного распределения одномерных случайных величин х, у и z задается в виде

где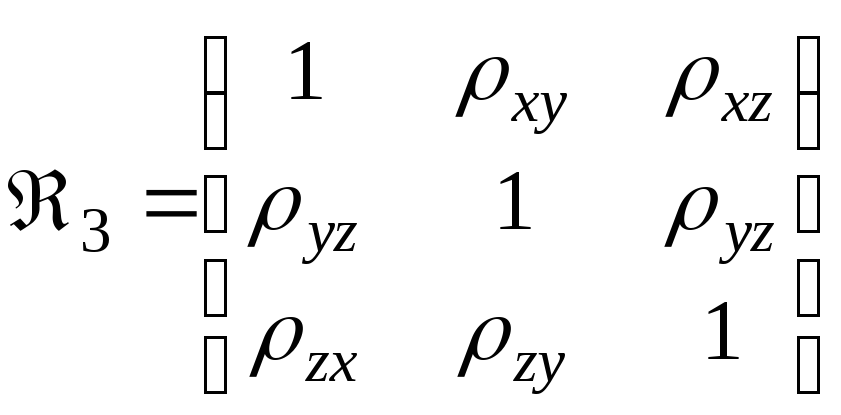— симметрическая положительно определенная матрица парных коэффициентов корреляции, соответствующих частным двумерным распределениям случайных величин(х,у), (х, z) и (y,z);

—определитель матрицы , обобщенная дисперсия случайной величины (х, у, z);

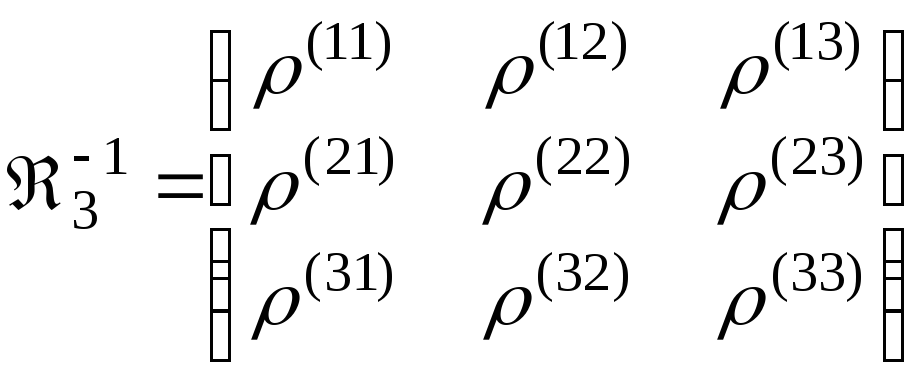- матрица, обратная :

- минор матрицы ,

дополнительный к

элементу _ji, j,i=1,2,3;

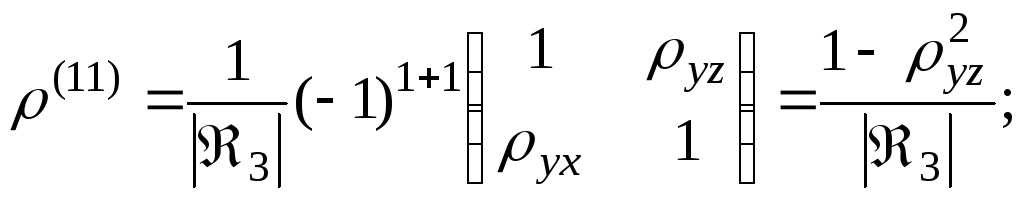
матрица — симметрическая, положительно определенная;

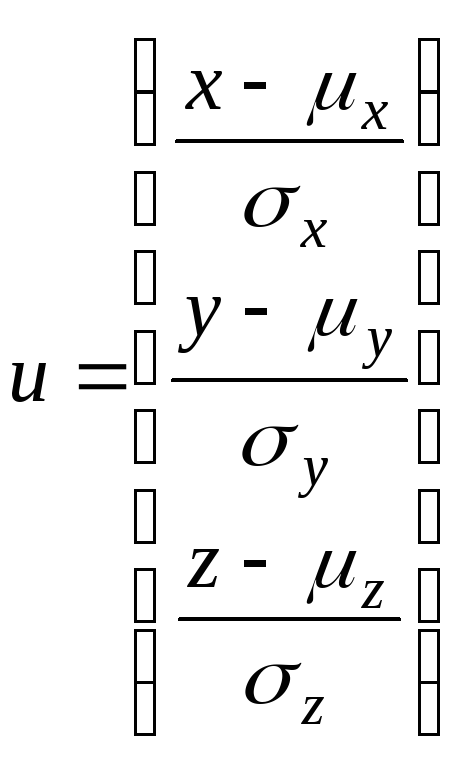- вектор значений нормированных случайных

величин x, y, z;

u^T — транспонированный вектор и:

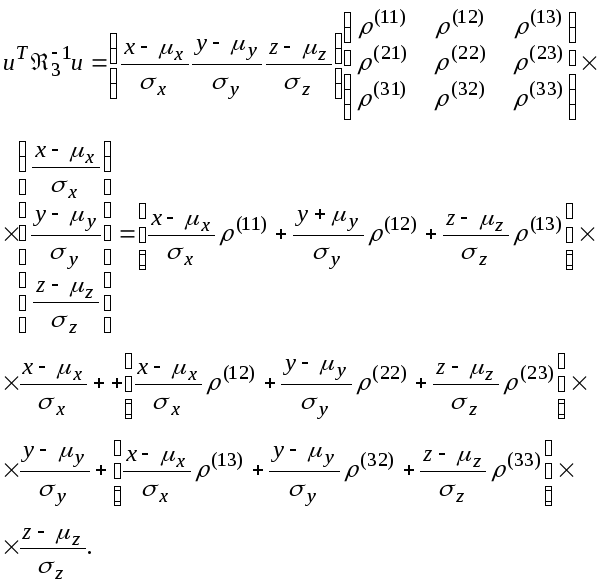
Таким образом, трехмерная нормально распределенная случайная величина определяется девятью параметрами:

тремя математическими ожиданиями:

тремя дисперсиями (или средними квадратическими отклонениями):

тремя парными коэффициентами корреляции:

Следует отметить, что частные одномерные (х, у и z), двумерные ((x,y),(x,z) и (y,z)) распределения компонент, а также условные распределения при фиксировании одной ((x,y)/z, (x,z)/y, (y,z)/x) и двух (х/у,z; у/хz; z/x,y) компонент являются нормальными. Поэтому поверхности и линии регрессии являются плоскостями и прямыми соответственно.

Для трехмерной (и других многомерных) корреляционной модели важную роль играют частные и множественные коэффициенты корреляции или детерминации (коэффициент детерминации равен квадрату соответствующего коэффициента корреляции).

Частным коэффициентом корреляции между х и у при фиксированных остальных компонентах (т. е. z) является выражение

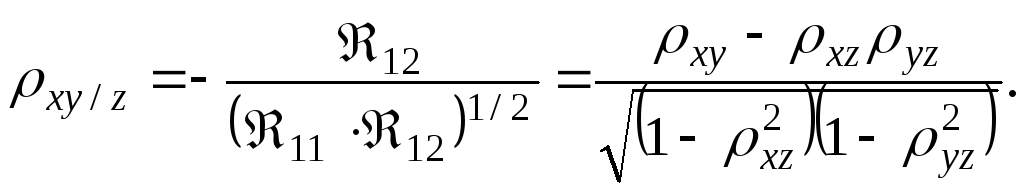(125)

Остальные частные коэффициенты корреляции _xz/y и _yz/x определяют путем замены соответствующих индексов в приведенных формулах.

Для нормального распределения частный коэффициент корреляции _xy/z совпадает с парным коэффициентом корреляции между величинами x и у при фиксированном z (в двумерном условном распределении ((x,y)/z). Частный коэффициент корреляции обладает всеми свойствами парного коэффициента корреляции.

Он служит показателем линейной связи между двумя переменными случайными величинами независимо от влияния остальных случайных переменных. Если частный коэффициент детерминации меньше, чем соответствующий парный коэффициент детерминации, то взаимозависимость между двумя величинами обусловлена частично (или целиком при равенстве нулю частного коэффициента детерминации) воздействием на эту пару остальных, фиксируемых, случайных величин. Если же, наоборот, частный коэффициент детерминации больше соответствующего парного, то фиксируемые величины ослабляют, затушевывают связь.

Множественный коэффициент корреляции между одной величиной z и двумя другими величинами (х,у) определяется по формуле

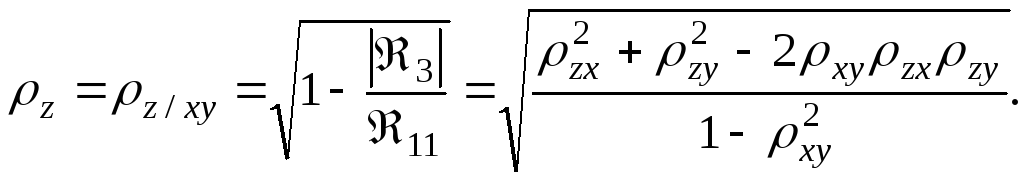(126)

Для трехмерной нормально распределенной случайной величины (x,y,z) множественный коэффициент корреляции является мерой связи между одной случайной величиной и двумя остальными. Он заключен между нулем и единицей. При _z = 1 связь между величинами z и (х,у) является функциональной, линейной: точки (x,y,z) расположены в плоскости регрессии z на (х,у). При _z = 0 одномерная случайная величина z и двумерная случайная величина (х,у) являются независимыми (в силу нормальности распределения). Множественный коэффициент детерминации показывает долю дисперсии случайной величины z, обусловленную изменением случайных величин (х,у).

Из определяющей _z формулы можно получить следующие неравенства:

Отсюда можно заметить, что коэффициент множественной корреляции может только увеличиться, если в модель включать дополнительные признаки — случайные величины, и не увеличиться, если из имеющихся признаков производить исключение.

Далее, если _z= 0, то _zx =_zy =_zx/y = _zy/x = 0.

Если, например, и, то и,. Последние неравенства можно получить исходя из формул:

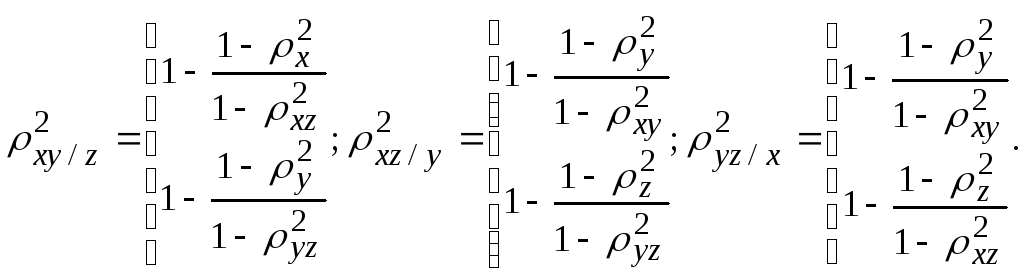
Таким образом, наибольшему множественному коэффициенту детерминации соответствуют большие частные коэффициенты детерминации (например, соответствуюти).

Приведем некоторые характеристики, подлежащие корреляционному анализу трехмерной случайной величины. При этом будем рассматривать лишь по одному условному распределению (двумерному и одномерному), так как остальные совпадают с рассматриваемыми с точностью до перестановки букв.