2.3.4. Проверка значимости параметров связи

В двумерной модели параметрами связи являются коэффициент корреляции  (или квадрат, называемый коэффициентом детерминации) и коэффициенты регрессии _yx и _xy.

Заметим, что в двумерной модели достаточно проверить значимость только коэффициента корреляции. Если коэффициент корреляции незначим, то признаки х и у считаются независимыми в генеральной совокупности.

Статистика r, вычисляемая для выборки из двумерной нормально распределенной совокупности с  = 0, связана со статистикой t, имеющей распределения Стьюдента с v=n-2 степенями свободы, формулой

(123)

Зная границы для t, соответствующие обычным уровням значимости (=10%, 5%, 2%, 1%), можно получить границы для r, воспользовавшись этой формулой. Границы для r табулированы. Таким образом, для проверки гипотезы H_{0: }=0 по данным  и v =п-2 находим r_табл . Если |r_набл | > r_табл , то гипотеза Но отвергается с вероятностью ошибки , если же |r_набл | < r_табл, то гипотеза не отвергается. При v> 100 для проверки H_{0: }=0 следует пользоваться нормированным нормальным законом распределения статистики

Если наблюдаемая величина (t или ) расположена в доверительном интервале[-t_1-, t_1-], то гипотеза Н₀ не отвергается; в противном случае H₀ отвергается с уровнем значимости .

2.3.5. Интервальные оценки параметров связи

Для значимых параметров связи имеет смысл найти интервальные оценки.

При нахождении доверительного интервала для коэффициента корреляции  используют статистику, введенную Фишером:

,

которая при n>10 распределена приблизительно нормально с

генеральным средним и дис

персией .

Тогда доверительный интервал, оценивающий MZ_r с надежностью =1-, имеет вид

(124)

где t_ — находится по таблицам интеграла Лапласа для данного  (или  =1-).

Для перехода от Z к  имеется таблица, составленная Фишером и Иейтсом, после использования которой получаем интервальную оценку с надежностью  вида

где r_min и r_max выбираются с учетом того, что Z_r — функция нечетная. При этом поправочным членом уMZ_r пренебрегают.

Если коэффициент корреляции значим, то коэффициенты регрессии также значимо отличаются от нуля (с тем же уровнем ). Интервальные оценки для них получаются по формулам:

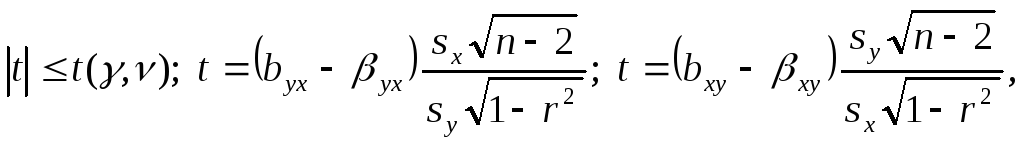
где t имеет распределение Стьюдента с v =n-2 степенями свободы.

Переход от неравенства |к интервальным оценкам для коэффициента регрессии осуществляется с помощью тождественных алгебраических преобразований.

Для значимого коэффициента корреляции  некоторые авторы рекомендуют более предпочтительную оценку, чем r:

Предпочтительной оценкой ² является выражение

Этими точечными оценками следует пользоваться при небольших объемах n выборки.

Кроме нахождения интервальной оценки для , с помощью преобразования

можно решить следующие задачи.

1. Проверить, согласуется ли выборочный коэффициент корреляции r с предполагаемым значением генерального коэффициента корреляции ₀. Для этого, взяв уровень значимости , проверяем, попадает ли абсолютная величина разности |Z_r -Z_ | в интервал [0,t1- /]. Если попадает, то гипотеза Н_0: =₀ не отвергается. В противном случае отвергается с уровнем .

1. Проверить гипотезу об однородности коэффициентов корреляции. Пусть r₁, r₂, ..., r_k. — коэффициенты корреляции, полученные из k нормально распределенных совокупностей по выборкам с объемами n₁, n₂, ..., n_k. Проверяется гипотеза

Статистика

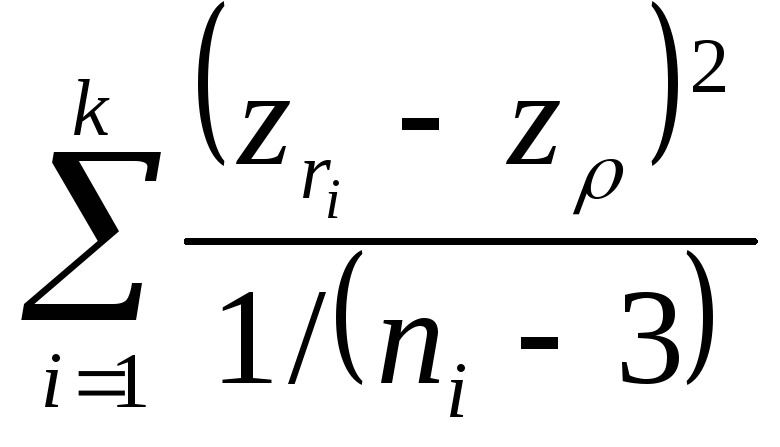
имеет тогда распределение ² с k степенями свободы. Если заменить z_ на среднее арифметическое

то получим, что

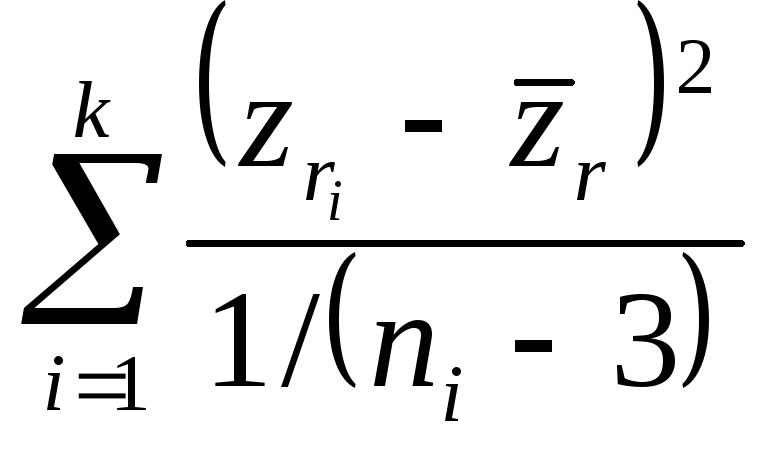
распределена по закону ² с v=k-1 степенями свободы. Если теперь для заданных а и v=k-1

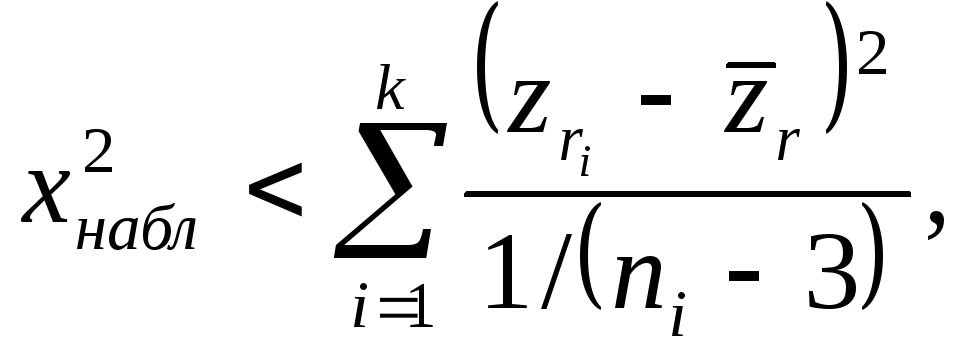
то гипотеза однородности отвергается с уровнем . В противном случае гипотеза Н₀ не отвергается.

В случае принятия гипотезы однородности предпочтительной точечной оценкой  является значение r, полученное обратным преобразованием из z_r.