7. Норма и число обусловленности матрицы

Матричная норма- это некоторая скалярная числовая характеристика, которую ставят в соответствие матрице. В задачах линейной алгебры используются раз­личные матричные нормы:

■ первая нормаквадратной матрицыА =:

■ вторая норма квадратной матрицыA={а_ij}:

где - максимальное собственное значение матрицыА;

■ евклидова норма квадратной матрицыА =:

■ бесконечная норма квадратной матрицы А:

Число обусловленности матрицы А используется для определения меры чув­ствительности системы линейных уравненийАх = b к погрешностям задания вектораb. Чем больше число обусловленности, тем более неустойчив процесс нахождения решения системы. Существует несколько вариантов нахождения числа обусловленности, но все они связаны с нормой матрицы и равны произ­ведению нормы исходной матрицы на норму обратной:

■ число обусловленности матрицы, вычисленное в норме :

■ число обусловленности матрицы, вычисленное в норме :

■ число обусловленности матрицы, вычисленное в норме :

■ число обусловленности матрицы, вычисленное в норме

ЗАДАЧА 13.

Вычислить нормы и числа обусловленности матрицы А.

В листинге приведен фрагмент документа, в котором происходит вы­числение норм матрицы А с помощью функцииnormи по соответствующим формулам.

Листинг 79

» А=[5 7 6 5;7 10 8 7;б 8 10 9;5 7 9 10]; \

» %Первая норма

» norm (АД)

ans =

33

» max(sum(abs(A)))

ans =

33

» % ---------------

» %Вторая норма »

norm(А,2)

ans =

30.2887

» sqrt(max(eig(A*A')))

ans =

30.2887

» % ----------------

» %Бесконечная норма

» norm(A,inf)

ans =

33

» max(sum(abs(A^’)))

ans =

33

» % ------------

» %Евклидова норма

» norm(A,'fro')

ans =

30.5450

» sqrt(sum(diag(A*A')))

ans =

30.5450

Значения чисел обусловленности отображены в следующем листинге. Их вычисле­ние было проведено при помощи функции cond(A) и по формулам, отражаю­щим зависимость числа обусловленности от соответствующей нормы матрицы.

Листинг 80.

» cond(A,l)

ans =

4.4880е+003

» norm(А,1)*norm(inv(A))

ans =

3.2512е+003

» norm(A,l)*norm(inv(A),1)

ans =

4.4880e+003

» cond(A,l)

ans =

4.4880e+003

» norm(A,l)*norm(inv(A),1)

ans =

4.4880e+003

» cond(A,2)

ans =

2.9841e+003

» norm(A,2)*norm(inv(A),2)

ans =

2.9841e+003

>> cond(A,inf) ans =

4.4880e+003

» norra(A,inf)*norm(inv(A),inf)

ans =

4.4880e+003

» cond(A,'fro')

ans =

3.0096e+003

» norm(A,'fro')*norm(inv(A) , 'fro')

ans =

3.0096e+003

8. Задания для самостоятельного решения

1.Для матрицА, В и С проверить выполнение следующих тождеств:

(А * В)* С= А * (В * Q и (А^Т+ В)*С=А^ТС+В* С, если:

A= 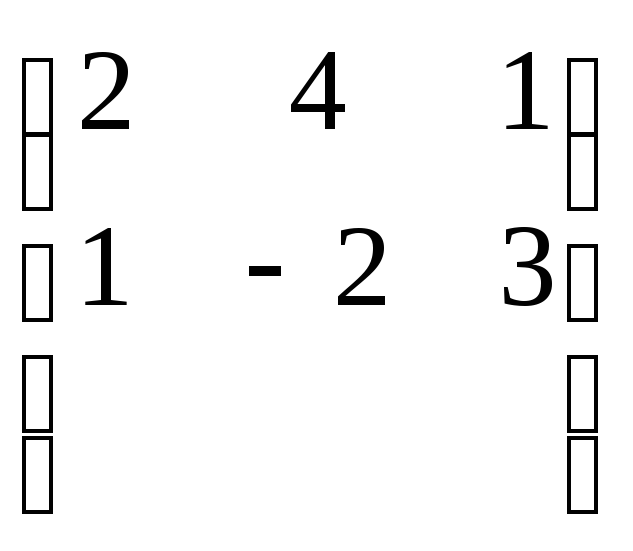, B=,C=

2.Выполнить действияА * (А²-В) - 2 *(В + А) * В над матрицами:

A=, =

3.Решить матричные уравнения АХ= В и ХА = В выполнить проверку, если:

A=B=

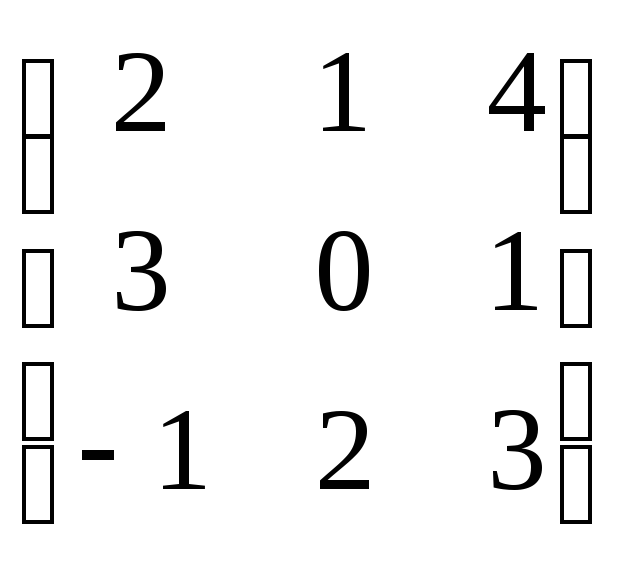
4.Решить систему линейных уравнений:

а) при помощи правила Крамера:

б) методом обратной матрицы:

в) методом Гаусса:

5. Найти собственные значения матрицы А:

A=

6. Привести заданную матрицу А (см. задание 5) к диагональному виду.

7. Вычислить нормы матрицы А (см. задание 5).

*Основное меню может отличаться от установленного на Вашем компьютере (здесь использована 32-битная версияMatlab^©ver. 7.11.0.584 (R2010b))

44