4. Амплитудная модуляция аналоговых сигналов

При ам­плитудной модуляции в соответствии с законом передаваемого со­общения меняется амплитуда модулируемого сигнала. Амплитудная модуляция - наиболее распространенный тип аналоговой модуляции в системах радиосвязи, радиовещания и телевидения.

Простейшая разновидность амплитудной модуляции -однотональная (от слова тон - звук одной частоты), при которой модулирующий сигнал представляет собой гармоническое колебание:

(39)

где - амплитуда модулирующего сигнала (максимальная высота синусоиды) ;

- круговая (угловая) частота, ;

- период модулирующего колебания;

- начальная фаза.

В качестве несущего колебания в системах связи и вещания практически всегда применяется высокочастотный гармонический сигнал.

Примем в качестве тестового аналогового сообщения синусои­дальный сигнал:

(40)

Несущие, т.е. модулируемые колебания

(41)

где частота несущих колебаний - частоты модулирующего колебания.

В результате воздействия колебания (40) на амплитуду несущих колебаний (41) получим сигнал с амплитудной модуляцией:

(42)

где - коэффициент амплитудной модуляции.

Графики трех названных колебаний приведены на рис. 13 и рис. 14.

Рис. 13.

Рис. 14

С целью наглядности на рис. 15, а, б изображены графики модулирующего колебания при , несущего – при.

1. Глубина амплитудной модуляции

Коэффициент (глубина) амплитудной модуляции (М) - коэффициент, равный отношению максимального приращения огибающей модулированных колебаний к амплитуде несущего колебания или отношению разности наибольшего и наименьшего значений модулированного сигнала к их сумме:

(47)

где - наибольшее, a- наименьшее значение, которого достигает амплитуда несущеговысокочастотного колебания при амплитудной модуляции – рис. 17.).

Это количественный параметр амплитудно-модулированных колебаний, характеризующий степень воздействия низкочастотного (модулирующего или управляющего) колебания (сигнала) на высокочастотное модулируемое или управляемое колебание (сигнал).

Рис. 17. Спектр однотонального амплитудно-

модулированного сигнала

Рис. 18. Спектр многотонального амплитудно-модулированного сигнала

Формулой (47) удобно пользоваться при экспериментальном определении коэффициента амплитудной модуляции, где чаще всего модуляция производится не гармоническим колебанием, а колебанием сложной формы [3].

В обычном режиме работы АМ-передатчик коэффициент в относительных единицах изменяется от 0 доили, если он измеряется в процентах, от 0 до 100 %. В этом случае амплитуда АМ-сигнала изменяется пределах от минимальнойдо максимальной.

Если , то возникает искажение АМ-сигнала, следовательно и передаваемого сообщения, называемогоперемодуляцией (Рис. 19), что может привести даже к потере передаваемой информации.

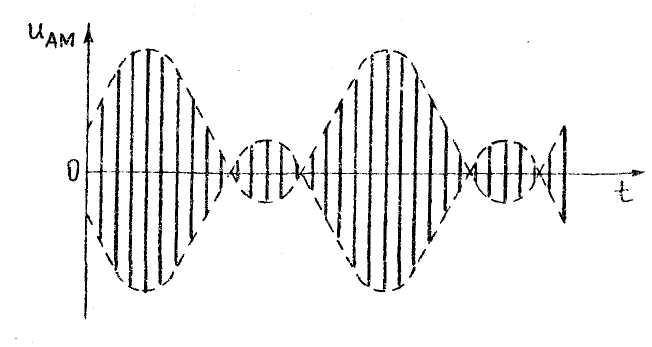
Рис. 19. Искаженный сигнал при перемодуляции

5. 1. Амплитудная модуляция цифровых сигналов

Примем в ка­честве тестового сообщения меандровый сигнал - последователь­ность битов с чередующимися 1 и 0 равной длительности (рис. 20,а). В результате наложения такого меандрового сигнала на несущие ко­лебания (41), получим модулированный сигнал (рис. 16,б).

Рассчитаем спектр меандра .

Спектральные составляющие можно также рассчитать по фор­муле:

(48)

где k - номер гармоники.

Из (48) и результатов расчета следует, что в спектре меандра содержатся только нечетные гармоники, т.е. частотой F, 3F, 5F и т.д., где F=1/T.

В результате амплитудной модуляции меандром несущие коле­бания приобретают вид, показанный на рис. 20,б.

При частоте несущих колебаний спектр модулированно­го сигнала подобен спектру меандра (рис. 21), но является почти симметричным и смещенным относительно начала координат на частоту f₀.

Амплитуда центральной спектральной со­ставляющей в этом спектре частотой равной 0,5АМ, а остальные спектральные составляющие уменьшены примерно в два раза по сравнению со спектром меандра.

Экзаменационный билет № 4

1. Импульсная модуляция

2. Виды детекторов и основные характеристики амплитудных детекторов. Особенности детектирования импульсных сигналов. Фазовые детекторы