- •Теоретический минимум к лабораторному практикуму по физике твердого тела
- •1. Элементы квантовой механики
- •1.1. Гипотеза де Бройля. Волновые свойства вещества
- •1.2. Соотношение неопределенностей
- •1.3. Уравнение Шрёдингера
- •1.4. Смысл пси-функции
- •1.6. Состояние электрона в атоме. Квантовые числа
- •1.7. Принцип Паули
- •2. Элементы квантовой статистики
- •2.1. Некоторые сведения из квантовой статистики
- •2.2. Вырожденный электронный газ в металлах
- •3. Элементы физики твердого тела
- •3.1. Понятие о зонной теории твердых тел
- •3.2. Металлы, полупроводники, диэлектрики
- •3.3. Собственная проводимость полупроводников
- •3.4. Примесная проводимость полупроводников
- •3.5. Контакт электронного и дырочного полупроводников (р-n переход)
- •3.6. Светодиоды
- •3.7. Фотопроводимость полупроводников
- •Библиографический список
- •Теоретический минимум к лабораторному практикуму по физике твердого тела
- •394026 Воронеж, Московский просп., 14
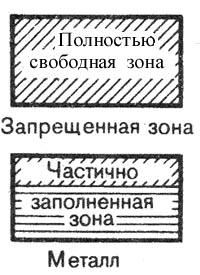
3.2. Металлы, полупроводники, диэлектрики
Зонная теория твердых тел позволила с единой точки зрения истолковать существование металлов, диэлектриков и полупроводников, объясняя различие в их электрических свойствах, во-первых, неодинаковым заполнением электронами разрешённых зон и, во-вторых, шириной запрещённых зон.
Степень заполнения энергетических уровней в зоне определяется заполнением соответствующих уровней в изолированных атомах. Если при этом какой-то энергетический уровень свободного атома полностью заполнен, то возникающая при образовании кристалла энергетическая зона так же заполнена целиком.
В общем случае можно говорить об энергетических зонах, которые полностью заполнены электронами и образованы из энергетических уровней внутренних электронов свободных атомов, и о валентных зонах, среди которых верхняя зона либо полностью заполнена электронами при Т = 0К, либо частично. Принято полностью заполненную электронами зону называтьвалентной зоной, а частично заполненную –свободной или зоной проводимости.
В зависимости от степени заполнения верхней зоны электронами и ширины последующей запрещённой зоны возможны следующие четыре случая распределения электронов, схематически представленные на рис. 3.6.
Если в энергетическом спектре валентных электронов твердого тела имеется зона, лишь частично заполненная электронами (рис. 3.6, а, б), то это тело являетсяпроводником электрического тока.
|
|
|
|
|
|
а) |
б) |
в) |
г) |
|
Рис. 3.6 | |||
В этом случае электрон, получив сколь угодно малую энергетическую «добавку», например, за счёт теплового движения или электрического поля, сможет перейти на более высокий энергетический уровень той же зоны, т.е. стать свободным и участвовать в проводимости. Внутризонный переход вполне возможен, так как, например, уже при Т = 1К энергия теплового движениякТ≈ 10-4эВ, что намного порядков больше разности энергий между соседними уровнями зоны, примерно равной 10-22эВ.
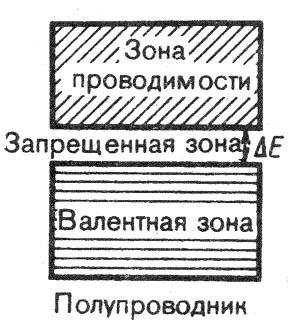
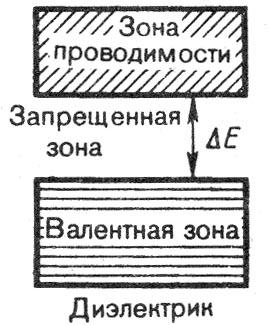
Твердые тела, у которых верхняя
энергетическая зона, содержащая
электроны, при Т= 0Кполностью
заполнена электронами, а последующая
разрешённая зона пуста (свободная зона)
являются или диэлектриками, или
полупроводниками, в зависимости от
ширины запрещённой зоны![]() между заполненной и свободной зонами
(рис. 3.6, в, г).
между заполненной и свободной зонами
(рис. 3.6, в, г).
Если запрещённая зона кристаллического
вещества достаточно мала (![]() порядка 1эВ), то переброс электронов
из валентной зоны в зону проводимости
может быть осуществлён либо путём
теплового возбуждения, либо за счёт
какого-либо внешнего источника, способного
передать электронам энергию
порядка 1эВ), то переброс электронов
из валентной зоны в зону проводимости
может быть осуществлён либо путём
теплового возбуждения, либо за счёт
какого-либо внешнего источника, способного
передать электронам энергию![]() ,
и вещество являетсяполупроводником(рис. 3.6,в). Если же ширина запрещённой
зоны
,
и вещество являетсяполупроводником(рис. 3.6,в). Если же ширина запрещённой
зоны![]() более 3эВ, то кристаллическое тело
является не проводником, т.е.диэлектриком(рис. 3.6,г).
более 3эВ, то кристаллическое тело
является не проводником, т.е.диэлектриком(рис. 3.6,г).
3.3. Собственная проводимость полупроводников
К собственным полупроводникам относят химически чистые полупроводники. Классическими примерами собственных полупроводников являются германий (Ge) и кремний (Si) высокой чистоты.
В собственных полупроводниках наблюдаются два механизма проводимости: электронный и дырочный.
При 0 Ки отсутствии других внешних факторов собственные полупроводники ведут себя как диэлектрики.
При повышении же температуры электроны с верхних уровней валентной зоны могут быть переброшены на нижние уровни зоны проводимости (рис. 3.7).
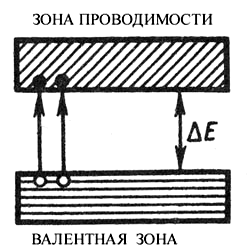
Рис. 3.7
При наложении на кристалл электрического поля электроны в зоне проводимости перемещаются против поля и создают электрический ток. Составляющая проводимости собственных полупроводников, обусловленная электронами, называется электронной проводимостьюилипроводимостью n-типа (от лат.negative– отрицательный).
В результате тепловых забросов электронов из валентной зоны в зону проводимости в валентной зоне возникают вакантные состояния, получившие название дырок. Во внешнем электрическом поле на освободившийся уровень валентной зоны (дырку) в одном месте кристалла может переместиться электрон с соседнего уровня и дырка появится в другом месте, откуда «ушёл» электрон и т.д. Такой процесс заполнения дырок электронами равносилен перемещению дырок в направлении, противоположном движению электронов, как если бы дырка была некоторой частицей и обладала положительным зарядом, равным по величине заряду электрона. Дырка представляет собой условную частицу, или, как говорят, квазичастицу. Составляющую проводимости собственных полупроводников, обусловленную квазичастицами – дырками называютдырочной проводимостьюилипроводимостью р-типа(от лат.positive– положительный).
Число электронов в зоне проводимости
равно числу дырок в валентной зоне.
Следовательно, в собственных полупроводниках
концентрация электронов в зоне
проводимости равна концентрации дырок
в валентной зоне
![]() .
.
Определенная концентрация электронов и дырок в полупроводнике при Т=constустанавливается в результате действия двух процессов – термическойгенерациисвободных носителей тока и ихрекомбинации. В полупроводнике происходит не только переброс электронов из валентной зоны в зону проводимости, но и переход электронов из зоны проводимости в валентную (дырочную) зону. При обратном переходе электрон и дырка связываются, и пара носителей уничтожается. Этот акт называют рекомбинацией носителей.
В собственном полупроводнике уровень Ферми при Т= 0Кнаходится в середине запрещённой зоны (рис. 3.8).

Рис. 3.8
Действительно, при появлении электрона
в зоне проводимости в валентной зоне
обязательно возникает дырка. Следовательно,
энергия активации
![]() ,
затраченная на образование пары
носителей тока, должна делиться на две
равные части, откуда
,
затраченная на образование пары
носителей тока, должна делиться на две
равные части, откуда
![]() .
.
Плотность тока
![]() при собственной проводимости полупроводника
складывается из плотности тока электронов
и дырок:
при собственной проводимости полупроводника
складывается из плотности тока электронов
и дырок:
![]() .
(3.1)
.
(3.1)
Обозначим равные друг другу концентрации
электронов и дырок
![]() и средние скорости упорядоченного
движения электронов и дырок
и средние скорости упорядоченного
движения электронов и дырок![]() и
и![]() .
Тогда
.
Тогда
![]() ,
,![]() .
(3.2)
.
(3.2)
Используя формулу закона Ома в дифференциальной форме
![]() ,
(3.3)
,
(3.3)
и формулы (3.2), получим:
![]() ,
(3.4)
,
(3.4)
затем, если разделить обе части (3.4) на
![]() и ввести подвижность электронов и дырок
и ввести подвижность электронов и дырок![]() и
и![]()
![]() и
и![]() , (3.5)
, (3.5)
то найдем
![]() .
(3.6)
.
(3.6)
Так как для собственных полупроводников
![]() ,
то распределение Ферми-Дирака (2.9)
переходит в распределение Максвелла-Больцмана
(2.3). Положив в (2.9)
,
то распределение Ферми-Дирака (2.9)
переходит в распределение Максвелла-Больцмана
(2.3). Положив в (2.9)![]() ,
,
получим
![]() .
(3.7)
.
(3.7)
Концентрация
![]() электронов и дырок, очевидно, пропорциональна
электронов и дырок, очевидно, пропорциональна![]() ,
т.е.
,
т.е.
![]() .
(3.8)
.
(3.8)
Подставляя (3.8) в (3.6), получим, что удельная проводимость собственных полупроводников быстро растёт с температурой, изменяясь по закону
![]() ,
(3.9)
,
(3.9)
где
![]() –
ширина запрещенной зоны,
–
ширина запрещенной зоны,![]() –
величина, изменяющаяся с температурой
гораздо медленнее, чем экспонента, в
связи с чем ее можно в первом приближении
считать постоянной.
–
величина, изменяющаяся с температурой
гораздо медленнее, чем экспонента, в
связи с чем ее можно в первом приближении
считать постоянной.
Логарифмируя (3.9), получим
![]() .
.
Видно, что зависимость
![]() от
от![]() линейная. Примерный график этой
зависимости приведён на рис. 3.9.
линейная. Примерный график этой
зависимости приведён на рис. 3.9.
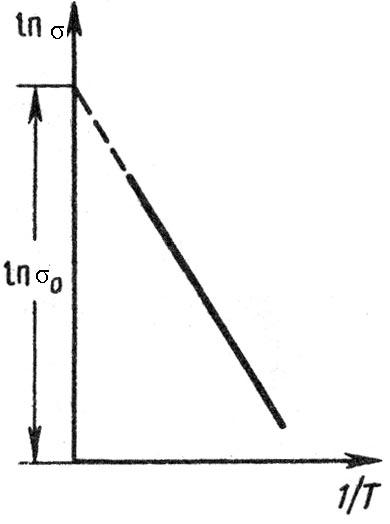
Рис. 3.9
По наклону отрезка прямой можно определить
ширину запрещенной зоны
![]() ,
а по пересечению продолжения прямой с
осью
,
а по пересечению продолжения прямой с
осью![]() –
величину
–
величину![]() (прямая отсекает на оси ординат отрезок,
равный
(прямая отсекает на оси ординат отрезок,
равный![]() ).
).