1.3. Уравнение Шрёдингера

В развитие идеи де Бройля о волновых свойствах частиц Шрёдингер в 1926 году предложил своё знаменитое уравнение. Шрёдингер сопоставил движущейся микрочастице комплексную функцию координат и времени, которую он назвал волновой функцией и обозначил греческой буквой «пси» . Её принято называть пси-функцией.

Состояние микрочастицы характеризует пси-функция, которая является решением уравнения Шрёдингера:

. (1.5)

Здесь m– масса частицы, i– мнимая единица,, – оператор Лапласа, результат действия которого на некоторую функцию представляет собой сумму вторых частных производных по координатам:

.

Символом U в уравнении (1.5) обозначена функция координат и времени, градиент которой, взятый с обратным знаком, определяет силу, действующую на частицу. В случае, когдаUне зависит явно от времени, она имеет смысл потенциальной энергии частицы.

В этом случае уравнение (1.5) преобразуется к виду

. (1.6)

Здесь ,Е– полная энергия частицы.

Уравнение (1.6) называется уравнением Шрёдингера для стационарных состояний.

В теории дифференциальных уравнений доказывается, что уравнения вида (1.6) имеют решения, удовлетворяющие стандартным условиям, налагаемым на -функцию, при дискретных значениях энергииЕ. Таким образом,квантование энергииполучается из основных положений квантовой механики без каких-либо дополнительных предположений.

1.4. Смысл пси-функции

Впервые правильная интерпретация пси-функции была дана Борном в 1926 году. Согласно Борну квадрат модуля пси-функции определяет вероятность того, что частица будет обнаружена в пределах объёма:

,

где А– постоянная нормирования,– квадрат модуля– функции,– функция, комплексно сопряжённая с.

Для нормированной – функциипостояннаяА= 1. В этом случае

. (1.7)

Из (1.7) следует, чтоквадрат модуля пси–функции имеет смысл плотности вероятности нахождения частицы в соответствующем месте пространства.

5. Туннельный эффект

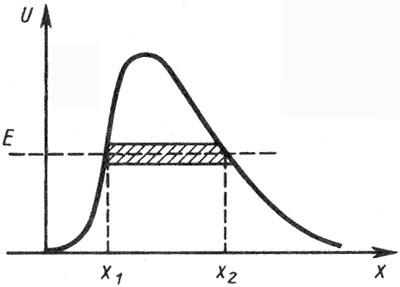
Туннельным эффектом называется прохождение частицы сквозь потенциальный барьер – ограниченную область пространства, где полная энергия Ечастицы меньше уровня потенциальной энергии. Туннельный эффект имеет квантовую природу и связан с наличием у частиц волновых свойств.

На рисунке представлена некоторая произвольная зависимость потенциальной энергии Uот координатыхчастицы в области одномерного потенциального барьера.

Коэффициентом прозрачности Dпотенциального барьера называется величина

,

где – интенсивность волны де Бройля, прошедшей сквозь потенциальный барьер,– интенсивность волны, падающей на барьер.

Для прямоугольного потенциального барьера

, (1.8)

где m– масса частицы,Е– ее энергия,L– ширина барьера.

Для потенциального барьера произвольной формы (рисунок).

. (1.9)

Согласно условию неопределенностикоординатыхчастицы будет соответствовать неопределенность импульса частицы, что не позволяет говорить об определенном значении кинетической энергиичастицы. Это значит, что неопределенность кинетической энергии частицы, вызванная фиксированием её координаты, превышает разность между высотой потенциального барьераи энергиейЕчастицы:

.

Неопределенность кинетической энергии частицы устраняет парадокс отрицательности кинетической энергии частицы в области потенциального барьера.