
- •1. Множества и бинарные отношения
- •Множества
- •Определения и примеры
- •1.1.1 Множество
- •Операции над множествами
- •Элементы комбинаторики
- •Бинарные отношения
- •Определения и примеры
- •2.1.2 Отображения
- •Операции над отношениями
- •Выполнение операций над отношениями
- •Свойства отношений
- •Эквивалентность и толерантность
- •2.4.1 Эквивалентность
- •2.4.3 Толерантность
- •2.4.6 Задача о наименьшем покрытии (ЗНП)
- •Алгоритм решения ЗНР
- •Отношения порядка
- •Строгий порядок
- •Свойства строгого порядка
- •Некоторые свойства дерева
- •Анализ отношений порядка
- •2.5.8 Решетки
- •2.5.10 Решетка
- •2.5.11 Булева решетка
- •Нормированные булевы решетки
- •Модели нормированной булевой решетки
- •Булевы функции (БФ)
- •Определения и примеры
- •Равенство булевых функций
- •3.3.1 СДНФ
- •3.3.3 СКНФ
- •3.3.5 Представление формул в СДНФ и СКНФ
- •Минимизация булевых функций
- •3.4.1 Импликанта
- •Полные системы булевых функций
- •2. Математическая логика
- •Логика высказываний
- •Основные понятия
- •4.1.7 Логическое следствие
- •4.1.8 Теоремы о логическом следствии
- •Логика предикатов
- •5.0.13 Связанные и свободные переменные
- •Предваренная нормальная форма
- •Стандартная нормальная форма
- •Подстановки и унификация
- •Метод резолюций для логики первого порядка
- •Исчисление высказываний
- •3. Графы
- •Определения и примеры
- •Определения графа
- •Части графа
- •Изоморфизм графов
- •Задание графов с помощью матриц
- •Матрица инциденций
- •Матрица соседства вершин
- •Матрица смежности
- •Типы графов
- •Обыкновенные графы
- •Графы Бержа
- •Помеченные и взвешенные графы
- •Другие способы задания графа
- •Связность графов
- •Маршруты, цепи, циклы
- •Число маршрутов
- •Компоненты связности
- •Нахождение компонент и бикомпонент
- •Кратчайшие цепи
- •Алгоритм Форда
- •Алгоритм Дейкстры
- •Обходы графа
- •Поиск в глубину на графе
- •Поиск в ширину на графе
- •Эйлеровы цепи и циклы
- •Эйлеровы пути
- •Гамильтоновы цепи и циклы
- •Цикломатика графов
- •Цикломатическое число
- •Деревья
- •Свойства дерева
- •Каркасы
- •Алгоритм нахождения каркаса графа.
- •Кратчайший каркас графа.
- •Алгоритм Прима.
- •Теорема о хорде каркаса.
- •Число каркасов графа.
- •Разрезы
- •Пространства суграфов
- •Пространство циклов
- •Пространство разрезов.
- •Потоки в сетях
- •Задача о максимальном потоке
- •Постановка задачи
- •Экстремальные части графа
- •Основные понятия
- •Покрытия
- •Задача о наименьшем покрытии
- •Паросочетания
- •Раскраска вершин графа
- •Хроматическое число
- •Оценки хроматического числа
- •Точные алгоритмы раскраски вершин

8.3. Каркасы |
249 |
|
|
|
|
Следовательно, граф имеет циклы, что противоречит определению дерева.
Свойство 5 следует из определения дерева; действительно, добавление ребра (разумеется, без добавления вершины) приводит к увеличению ¸ на единицу, то есть к появлению цикла.
Свойство 6 можно проверить непосредственно, учитывая, что в дереве нет циклов.
Свойство 7 следует из свойства 6 и теоремы 2.3 (вершины, не являющиеся точками сочленения, есть висячие вершины). £
Свойство 4 можно представить в следующей форме:
Теорема 8.4 Конечный неориентированный граф является деревом тогда и только тогда, когда для любых его вершин x; y существует цепь из x в y, притом простая и единственная.
При x = y эта цепь имеет нулевую длину.
Следствие. Из любого графа G можно удалить ¸(G) ребер так, чтобы полученный суграф T не имел циклов и обладал тем же числом компонент связности, что и G. Всякий же суграф, полученный из G удалением менее чем ¸(G) ребер имеет циклы.
8.3 Каркасы
Изучение графов без циклов позволит нам выяснить смысл цикломатического числа в тех случаях, когда оно отлично от нуля.
Определение. Всякий суграф T графа G, у которого
m(T ) = m(G) ¡ ¸(G);
·(T ) = ·(G);
¸(T ) = 0;
называется каркасом графа G
(синонимы: oстов,´ стягивающее дерево, spanning tree, ST).
В определении каркаса любые два условия влекут третье, в силу равенства n(T ) = n(G) и определению цикломатического числа.
Существование хотя бы одного каркаса у каждого графа следует из свойств дерева и следствий из них. Справедлива и более сильная теорема о существовании каркаса.
250 |
Глава 8. Цикломатика графов |
|
|
Теорема 8.5 (теорема Коцига). Пусть T 0 – произвольный связный суграф графа G, не имеющий циклов. Тогда у графа G есть по крайней мере один каркас T , содержащий все ребра T 0 (т.е. T 0 является суграфом T ).
Д о к а з а т е л ь с т в о . Если данный граф G не содержит циклов, то он сам и есть искомый каркас, то есть T = G; так как при ¸(G) = 0 граф G, по определению, каркас. Если же ¸(G) > 0; то в G найдется цикловое ребро, не принадлежащее суграфу T 0 (иначе T 0 имел бы циклы). Удаление этого ребра из G уменьшит ¸(G) на единицу; при этом ·(G) не изменится. Если в полученном суграфе еще есть циклы, то снова удалим цикловое ребро, не принадлежащее T 0 и т.д. После ¸(G) таких шагов получим искомый каркас T . £
8.3.1Алгоритм нахождения каркаса графа.
Вэтом алгоритме мы воспользуемся той же разметкой, которую мы применяли для нахождения кратчайшей цепи в связном графе.
Шаг 1. Выберем произвольную вершину и пометим ее меткой 0. Шаг 2. Все непомеченные вершины, смежные с вершинами, имеющими метку k, помечаем меткой k + 1: Разметка продолжается до тех пор, пока все вершины не будут помечены. При такой разметке метки смежных вершин не могут отличаться более чем на единицу.
Шаг 3. После окончания разметки будем просматривать вершины в любом порядке и удалять некоторые ребра по следующим правилам:
²если в данный момент мы находимся в вершине x с меткой l(x), то удаляем все те еще не удаленные ранее ребра, которые соединяют x с вершинами, имеющими ту же метку;
²из ребер, соединяющих x с вершинами, имеющими метку l(x) ¡ 1, удаляем все, кроме любого одного.
Покажем, что суграф T , оставшийся после такого удаления ребер, является каркасом.
1. ·(T ) = ·(G), так как правила удаления таковы, что разметка сохраняется и для суграфа T . Поэтому число вершин, соединимых с вершиной, имеющей метку 0, одинаково в T и в G.

8.3. Каркасы |
251 |
|
|
|
|
2. Разметка такова, что ребро между двумя вершинами с одинаковыми метками – цикловое. Далее, мы отыскиваем для каждой вершины единственную цепь, соединяющую эту вершину с вершиной, имеющей метку 0, отсекая все другие возможные цепи.
Пример 8.1.
|
|
|
G |
|
|
|
|
T |
|
|
0 |
|
1 |
|
2 |
|
|
|
|
||
|
r |
¡ |
r |
A |
|
r |
r |
r |
A |
r |
|
|
¡ A |
ArA |
|
|
r@ |
A |
|
ArA |
|
|
¡ |
|
|
|
|
|
|
|||
1 |
r@ |
|
2 |
|
|
|
|
|||
|
r |
@@r |
|
AA |
r |
r |
@@r |
|
AAr |
|
2 |
|
2 |
|
3 |
|
|
|
|
||
Граф G и один из его возможных каркасов T (на графе G указана разметка для нахождения каркаса). J
8.3.2Кратчайший каркас графа.
Рассмотрим связный обыкновенный граф со взвешенными ребрами G = (X; U); вес ребра (xi; xj) обозначим через cij или c(xi; xj). Если нет ребра (xi; xj), то c(xi; xj) = 1.
Задача заключается в том, чтобы из всех каркасов графа найти один такой, что сумма весов его ребер – наименьшая. Назовем такой каркас кратчайшим (shortest spannig tree –SST). Задача нахождения SST возникает, например, в том случае, если какие-либо пункты (города, дома в городе, клеммы электрической сети и т.д.) нужно связать кратчайшей сетью коммуникаций (трубопроводов, электрических проводов, дорог и т.д.). Задача нахождения кратчайшего каркаса (SST ) – это одна из немногих задач теории графов, которую можно считать полностью решенной.
Подход к построению алгоритма нахождения SST состоит в следующем. Пусть в процессе построения SST уже построены его поддеревья
T1; T2; : : : ; Tk
с соответствующими подмножествами вершин
X1; X2; : : : ; Xk:
252 |
Глава 8. Цикломатика графов |
|
|
Для двух поддеревьев Ti; Tj рассмотрим все соединяющие их ребра, если они имеются, и выберем кратчайшее из них (с наименьшим весом), т.е. ребро с весом
min [min c(x |
; x )]; i = j: |
|||
¢ij = xi |
Xi |
i |
j |
6 |
|
2 |
|
|
|
Покажем, что это ребро принадлежит SST , и деревья Ti и Tj можно срастить в одно поддерево с включением этого ребра.
Д о к а з а т е л ь с т в о (от противного). Пусть на некоторой итерации алгоритма, например, на k-й, построены поддеревья, принадлежащие окончательному SST , а ребро (x?i ; x?j ) – кратчайшее между деревьями Ti; Tj, в SST не содержится. Так как в конце концов деревья Ti и Tj должны быть связаны, то в SST должно существовать некоторое ребро (xi; xj), такое, что, xi 2 Xi; xj 2 Xj. Если теперь мы удалим ребро (xi; xj) и добавим ребро (x?i ; x?j ), то получим новое дерево, более короткое, чем SST , что противоречит определению SST .
Таким образом, ребро (x?i ; x?j ) можно добавить к частично сформированному на k-й итерации SST . Заметим, что результат не зависит от выбора поддеревьев Ti; Tj. Поскольку на начальном этапе (пока еще никакие ребра не выбраны) предположение о принадлежности ребер к SST автоматически выполнено, то многократно выбирая кратчайшие ребра, в конце концов получим SST . £
8.3.3 Алгоритм Прима.
Алгоритм строит кратчайший каркас, который начинается с одной вершины и разрастается при добавлении на каждой итерации по одному ребру. Вершины при этом рассматриваются как отдельные поддеревья кратчайшего каркаса. Поддерево T постепенно разрастается за счет добавления ребер (x; y), где x 2 T , а y 62T ; при этом добавляемое к каркасу ребро должно иметь наименьший вес c(x; y). Процесс продолжается до тех пор, пока число ребер в T не станет равным n ¡ 1. Тогда дерево T и будет искомым
SST .
В алгоритме применяется разметка вершин, очень похожая на ту, которая используется в алгоритме Дейкстры нахождения кратчайшей цепи.
Обозначения :
Y – текущее множество вершин, входящих в SST ;
V – текущее множество ребер, входящих в SST ;
8.3. Каркасы |
253 |
|
|
|
|
Составная метка вершины x имеет вид [ p(x); l(x)]; здесь p(x) – метка предшествования: вершина, предшествующая x и определяющая ребро (p(x); x), а l(x) – метка, соответствующая весу этого ребра.
Представим алгоритм в следующем виде. Шаг 1. Инициализация.
Y := fyg; (y – произвольно выбранная вершина )
p(y) := y; l(y) := 0;
V = Â;
Шаг 2. Для каждой вершины x 62Y найти вершину q 2 Y , такую,
что
c(q; x) = min[c(z; x)];
z2Y
p(x) := q; l(x) := c(q; x);
Если такой вершины нет, т.е. x несмежна с вершинами из Y , то
p(x) := x; l(x) := 1;
Под 1 здесь понимается любое число, заведомо большее, чем вес любого из ребер графа G.
Шаг 3. Выбрать такую вершину z, что
l(z) = min [ l(x)]
z62Y
(Вершина z – ближайшая к уже построенному поддереву SST ).
(Обновить данные).
Y := Y [ fzg; V := V [ f(p(z); z)g;
Если jY j = n, то останов; ( Ребра из V образуют SST ). Если jY j < n, то на Шаг 4.
Шаг 4. Для всех x 62Y , таких, что x 2 ¡z (смежных с вершиной z) обновить метки следующим образом :
если l(x) > c(z; x), то l(x) := c(z; x); p(x) := z;
на Шаг 3. Пример 8.2.
Пусть задан граф
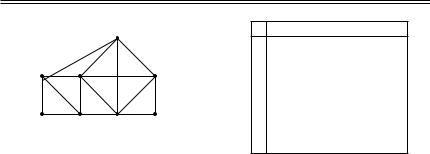
254 |
|
|
|
Глава 8. |
Цикломатика графов |
||||||||
|
|
3 |
|
C |
1 |
2 |
3 |
4 |
5 |
6 |
|
7 |
8 |
|
|
|
|
|
|||||||||
|
|
|
|
1 |
0 |
3 |
4 |
1 1 1 |
7 |
2 |
|||
|
|
|
4 |
2 |
3 |
0 |
5 |
6 |
1 |
8 |
|
8 |
1 |
1 |
2 |
|
3 |
4 |
5 |
0 |
9 |
1 2 |
|
1 1 |
|||
|
|
|
C = 4 1 6 |
9 |
0 |
9 |
3 |
1 1 |
|||||
|
|
|
|
5 |
1 1 1 |
9 |
0 |
3 |
|
1 1 |
|||
|
|
|
|
6 |
1 8 |
2 |
3 |
3 |
0 |
|
9 |
1 |
|
8 |
7 |
6 |
5 |
7 |
7 |
8 |
1 1 1 9 |
|
0 |
5 |
|||
|
|
|
|
8 |
2 |
1 1 1 1 1 |
5 |
0 |
|||||
с матрицей весов C.
Требуется найти кратчайший каркас. Действуем в соответствии с предписаниями алгоритма.
|
?1 |
|
?3 |
?4 |
?6 |
?7 |
?5 |
|
?2 |
|
|
Y |
1 |
|
2 |
3 |
4 |
5 |
6 |
7 |
8 |
V C |
|
|
|
|
|
|
|
|
|
||||
1 |
[1; 0] |
[1; 3] [1; 4] |
[4; 1] [5; 1] |
[6; 1] [1; 7] |
[1; 2] |
(1; 8) |
2 |
||||
8 |
£ |
|
[1; 3] [1; 4] |
[4; 1] [5; 1] |
[6; 1] |
[8; 5] |
£ |
(1; 2) |
3 |
||
2 |
£ |
|
£ |
[1; 4] |
[2; 6] [5; 1] |
[2; 8] [8; 5] |
£ |
(1; 3) |
4 |
||
3 |
£ |
|
£ |
£ |
[2; 6] [5; 1] |
[3; 2] |
[8; 5] |
£ |
(3; 6) |
2 |
|
6 |
£ |
|
£ |
£ |
[6; 3] |
[6; 3] |
£ |
[8; 5] |
£ |
(6; 4) |
3 |
4 |
£ |
|
£ |
£ |
£ |
[6; 3] |
£ |
[8; 5] |
£ |
(6; 5) |
3 |
5 |
£ |
£ |
£ |
£ |
£ |
£ |
[8; 5] |
£ |
(8; 7) 5 |
||
Примечания.
Шаг 1. Y := f1g: Выбираем произвольную вершину 1. p(1) = 1; l(1) = 1:
Отмечаем вершину 1 как вошедшую в каркас с номером 1 знаком
?1.
V = Â ; Суммарный вес каркаса C = 1: Шаг 2. Помечаем вершины 2, 3, 7, 8.
p(2) := 1; l(2) := 3; p(3) := 1; l(3) := 4; p(7) := 1; l(7) := 7; p(8) := 1; l(8) := 2;
Остальные метки: p(x) := x; l(x) := 1.
Шаг 3. Наименьшая метка l(x) – у вершины 8 ;
Y := f1g [ f8g; V := f(1; 8)g; Отмечаем вершины 1 и 8, как включенные в Y . Длина ребра (1,8) равна 2. Текущей вершиной z становится вершина 8. Отмечаем вершину 8 (как новый элемент Y ) знаком ?2.
Шаг 4. Для всех вершин, смежных с вершиной 8, обновляем метки:
8.3. Каркасы |
255 |
|
|
|
|
p(7) := 8; l(7) := 5. Остальные метки остаются прежними. На
Шаг 3.
Шаг 3. Наименьшая метка l(x) – у вершины 2;
Y := f1; 8; 2g; V := f(1; 8); (1; 2)g; c := 3; z := 2:
Отмечаем вершину 2 (как элемент Y ) знаком ?3.
Шаг 4. Обновляем метки: p(4) := 2; l(4) := 6; p(6) := 2; l(6) := 8:
Остальные метки остаются прежними. Шаг 3. Наименьшая метка l(x) – у вершины 3.
Y = f1; 8; 2; 3g; V = f(1; 8); (1; 2); (1; 3)g; c := 4; z := 3:
Отмечаем вершину 3 (как элемент Y ) знаком ?4.
Шаг 4. Обновляем метки: p(6) := 3; l(6) := 2: Остальные метки остались прежними.
Шаг 3. Наименьшая метка l(x) – у вершины 6.
Y := f1; 8; 2; 3; 6g; V := f(1; 8); (1; 2); (1; 3); (3; 6)g; c := 2; z := 6:
Отмечаем вершину 6 знаком ?5.
Шаг 4. Обновляем метки: p(4) := 6; l(4) := 3; p(5) := 6; l(5) := 3:
Остальные метки без изменений.
Шаг 3.Наименьшая метка l(x) – у вершины 4.
Y := f1; 8; 2; 3; 6; 4g; V := f(1; 8)6; (1; 2); (1; 3); (3; 6); (6; 4)g; c := 3; z := |
||
4: Отмечаем вершину 4 знаком ? . |
||
Шаг |
4. |
Все метки остаются без изменений. |
Шаг |
3. |
Наименьшая метка l(x) – у вершины 5; |
Y := f1; 8; 2; 3; 6; 4; 5g; V := f(1; 8); (1; 2); (1; 3); (3; 6); (6; 4); (6; 5)g; c := 3; z := 5:
Отмечаем вершину 5 знаком ?7.
Шаг 4. Все метки остаются без изменений. Шаг 3. Наименьшая метка l(x)– у вершины 7.
Y := f1; 8; 2; 3; 6; 4; 5g; V := f(1; 8); (1; 2); (3; 6); (6; 4); (6; 5); (8; 7)g; c := 5; jY j = 8 = n:
Суммарный вес : 22. Кратчайший каркас приведен на рисунке.
|
|
|
|
3 |
|
|
|
1 |
|
|
|
|
|
4 |
|
|
|
|
|
|
|||
|
2 |
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
8 |
7 |
6 |
5 |
||||
J
