
- •1. Множества и бинарные отношения
- •Множества
- •Определения и примеры
- •1.1.1 Множество
- •Операции над множествами
- •Элементы комбинаторики
- •Бинарные отношения
- •Определения и примеры
- •2.1.2 Отображения
- •Операции над отношениями
- •Выполнение операций над отношениями
- •Свойства отношений
- •Эквивалентность и толерантность
- •2.4.1 Эквивалентность
- •2.4.3 Толерантность
- •2.4.6 Задача о наименьшем покрытии (ЗНП)
- •Алгоритм решения ЗНР
- •Отношения порядка
- •Строгий порядок
- •Свойства строгого порядка
- •Некоторые свойства дерева
- •Анализ отношений порядка
- •2.5.8 Решетки
- •2.5.10 Решетка
- •2.5.11 Булева решетка
- •Нормированные булевы решетки
- •Модели нормированной булевой решетки
- •Булевы функции (БФ)
- •Определения и примеры
- •Равенство булевых функций
- •3.3.1 СДНФ
- •3.3.3 СКНФ
- •3.3.5 Представление формул в СДНФ и СКНФ
- •Минимизация булевых функций
- •3.4.1 Импликанта
- •Полные системы булевых функций
- •2. Математическая логика
- •Логика высказываний
- •Основные понятия
- •4.1.7 Логическое следствие
- •4.1.8 Теоремы о логическом следствии
- •Логика предикатов
- •5.0.13 Связанные и свободные переменные
- •Предваренная нормальная форма
- •Стандартная нормальная форма
- •Подстановки и унификация
- •Метод резолюций для логики первого порядка
- •Исчисление высказываний
- •3. Графы
- •Определения и примеры
- •Определения графа
- •Части графа
- •Изоморфизм графов
- •Задание графов с помощью матриц
- •Матрица инциденций
- •Матрица соседства вершин
- •Матрица смежности
- •Типы графов
- •Обыкновенные графы
- •Графы Бержа
- •Помеченные и взвешенные графы
- •Другие способы задания графа
- •Связность графов
- •Маршруты, цепи, циклы
- •Число маршрутов
- •Компоненты связности
- •Нахождение компонент и бикомпонент
- •Кратчайшие цепи
- •Алгоритм Форда
- •Алгоритм Дейкстры
- •Обходы графа
- •Поиск в глубину на графе
- •Поиск в ширину на графе
- •Эйлеровы цепи и циклы
- •Эйлеровы пути
- •Гамильтоновы цепи и циклы
- •Цикломатика графов
- •Цикломатическое число
- •Деревья
- •Свойства дерева
- •Каркасы
- •Алгоритм нахождения каркаса графа.
- •Кратчайший каркас графа.
- •Алгоритм Прима.
- •Теорема о хорде каркаса.
- •Число каркасов графа.
- •Разрезы
- •Пространства суграфов
- •Пространство циклов
- •Пространство разрезов.
- •Потоки в сетях
- •Задача о максимальном потоке
- •Постановка задачи
- •Экстремальные части графа
- •Основные понятия
- •Покрытия
- •Задача о наименьшем покрытии
- •Паросочетания
- •Раскраска вершин графа
- •Хроматическое число
- •Оценки хроматического числа
- •Точные алгоритмы раскраски вершин
2.5. Отношения порядка |
97 |
|
|
|
|
q4
q3
q2
q1
a
|
|
f1; 2; 3g |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
¡¡@q@ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
¡ |
|
|
@ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
f1; 2g |
¡ |
|
f1; 3g@f2; 3g |
|
1; 2 |
|
|
1; 3 |
|
|
2; 3 |
|
|||||||||
|
|
q@@ ¡¡@q@ ¡¡q |
|
|
f |
|
|
g f |
|
g f |
|
|
q |
g |
|||||||
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
¡@ ¡@ |
|
|
|
|
|
q@@ ¡¡@q |
@¡¡ |
|
|
||||||||||
|
|
¡ |
@¡ |
@ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
1 |
|
q@@ |
|
q2 |
g¡ |
¡¡q |
3 |
|
|
|
¡¡@@¡¡@@ |
|
|
|
|||||||
|
|
|
|
|
|
|
|
||||||||||||||
f |
g |
@ |
|
f |
|
f |
g |
|
1q |
|
|
2q |
|
|
3q |
|
|||||
|
|
|
@¡ |
|
|
|
|
f g |
f g |
f g |
|||||||||||
|
|
|
?q |
|
|
|
|
|
|
|
|
|
c |
|
|
|
|
|
|
||
|
|
|
b |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
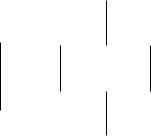
Рис. 2.15. Диаграммы Хассе
2. Семейство
B(f1; 2; 3g) = f?; f1g; f2g; f3g; f1; 2g; f1; 3g; f2; 3g; f1; 2; 3gg
упорядочено отношением включения µ. Диаграмма Хассе представлена на рис. 2.15, b.
3. Семейство множеств A = ff1g; f2g; f3g; f1; 2g; f1; 3g; f2; 3gg упорядочено отношением включения µ. Диаграмма Хассе для этого упорядоченного множества представлена на рис. 2.15, c. J Любая точка, из которой нет восходящей линии – это один из максимальных элементов множества, и если такая точка только одна, она представляет наибольший элемент
множества.
Точки, из которых не исходят нисходящие линии, представляют минимальные элементы (если он один, то наименьший).Наибольший (наименьший) элемент представляет точную верхнюю (нижнюю) грань этого множества.
Пусть h4; Mi – частично упорядоченное Решетка множество.
Определение. h4; Mi является решеткой тогда и только тогда, когда каждая пара элементов a; b 2 M имеет точную верхнюю и точную нижнюю границы.
Обозначим supfa; bg = a _ b; inffa; bg = a ^ b. Тогда определение решетки можно записать так:
8a; b 2 M[9!i = a ^ b; i 2 M & 9!s = a _ b; s 2 M]

98 |
Глава 2. Бинарные отношения |
|
|
где 9! означает “существует один и только один".
Операции ^ и _ можно также рассматривать как отображения M £ M в M, которые каждой паре ha; bi (a; b 2 M) ставят в соответствие элементы a _ b; a ^ b.
Пусть a; b; c 2 M. Можно доказать, что решетка обладает следующими свойствами.
1.a _ b = b _ a; a ^ b = b ^ a (коммутативность);
2.a_(b_c) = (a_b)_c; a^(b^c) = (a^b)^c (ассоциативность);
3.a _ a = a; a ^ a = a (идемпотентность);
4.a _ (a ^ b) = a; a ^ (a _ b) = a (поглощение);
Определение. Решетка h4; Mi дистрибутивна, если для всех a; b; c 2 M
a _ (b ^ c) = (a _ b) ^ (a _ c); a ^ (b _ c) = (a ^ b) _ (a ^ c).
Примеры 2.34.
1. Нетрудно проверить, что решетки на рис. 2.16. дистрибутивны:
|
|
|
|
|
|
f1; 2; 3g |
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
¡ |
|
r@ |
|
|
|
|
|
|
|
f |
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
r |
4 |
1; 2 ¡¡ |
|
|
|
1@; 3@2; 3 |
d |
|
©©©raaa |
e |
||||||||||
|
|
|
|
||||||||||||||||||
|
|
|
|
|
|||||||||||||||||
|
3 |
f |
|
@ |
|
|
|
r |
|
g |
|
|
r |
, r |
|
||||||
|
|
¡@ ¡ |
|
|
|
||||||||||||||||
|
|
g |
|
|
|
f |
|
|
gf |
|
|
|
|
, |
|
|
|||||
|
r |
|
|
|
r |
¡@ |
r |
|
¡@ |
|
|
|
|
|
|
, |
|
|
|||
|
r2 |
|
¡ |
@¡ @ |
|
|
|
|
|
,, |
|
|
c |
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
r |
1 |
1 |
|
r@ |
|
r2 |
g¡ |
¡r |
3 |
g |
b |
HHH!!! |
|
||||||||
|
f |
g |
@ |
f |
|
f |
|
r |
r |
|
|||||||||||
|
|
|
|
|
|
@¡¡ |
|
|
|
|
|
|
|
ar |
|
||||||
|
|
|
|
|
|
|
?r |
|
|
|
|
|
|
|
|
|
|
|
|
||
Рис. 2.16. Дистрибутивные решетки
2. Решетка hµ; f?; f1g; f2g; f3g; f1; 2; 3ggi (рис. 2.17.) недистрибутивна. Действительно,
f1g _ (f2g ^ f3g) = f1g _ ? = f1g;
(f1g _ f2g) ^ (f1g _ f3g) = f1; 2; 3g _ f1; 2; 3g = f1; 2; 3g. Заметим, что для этой решетки операции _; ^ не могут
быть интерпретированы как теоретико-множественные операции [ и \.
2.5. Отношения порядка |
99 |
|
|
|
|
f1; 2q; 3g
¡@
¡@
¡@
f1g |
¡ |
fq2g |
@ |
@q |
¡qf3g |
@¡
@¡
@¡q
?
Рис. 2.17. Недистрибутивная решетка
3.Линейно упорядоченное множество является решеткой (дистрибутивной).
4.Контрпримеры: понятие отношения порядка не равносильно понятию решетки:
d |
|
|
fq |
|
|
e |
d |
|
|
e |
gq |
|
f |
||||||
|
q |
|
q |
|
|
|
q |
|
q |
|
q |
||||||||
b |
|
q |
aq |
|
q |
c |
b |
|
q |
aq |
|
|
|
|
|
|
q c |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
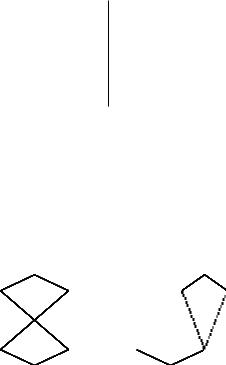
Рис. 2.18. Эти множества не являются решетками
На левой диаграмме пара элементов hd; ei имеет не единственную нижнюю грань: d ^ e = fb; cg. На правой диаграмме пара элементов hd; ei не имеет верхней грани. J
Определение. Если h4; Mi – решетка и M имеет наименьший и наибольший элементы, то решетка называется ограниченной. Обозначим через 1 верхнюю грань всей решетки, а через 0 – нижнюю грань всей решетки.
Определение. Ограниченная решетка h4; Mi называется
решеткой с дополнениями, если для каждого a 2 M существует такой элемент a¹ 2 M, что a _ a¹ =1 и a ^ a¹ =0.
Элемент a¹ называется дополнением элемента a. Пример 2.35. Для решетки, приведенной на рисунке 2.19:
¹ ¹ ¹ ¹ ¹
0 = 1; 1 = 0; a¹ = d; b = d; c¹ = d; d = a; d = c:

100 |
Глава 2. Бинарные отношения |
|
|
1q
AA
a¡q AA
¡A
¡A
b ¡q qc Aq d
@¡
@¡
@¡
@q¡
0
Рис. 2.19. Ограниченная решетка
Определение. Решетка h4; Mi называется решеткой с единственным дополнением, если для каждого элемента a 2 M существует только одно дополнение.
Примером решетки с единственным дополнением может служить
hµ; B(f1; 2; 3g)i.
Определение. Булева решетка– это дистрибутивная решетка с единственным дополнением.
(выполняются законы двойного дополне-
ния и де Моргана: a¹ |
|
|
¹ |
|
¹ |
|
|
||||
= a, a _ b = a¹ ^ b, a ^ b = a¹ _ b). |
|||||
Конечная булева решетка и решетка hµ; B(U)i изоморфны.
Запишем булеву решетку в виде
hB; +; ¢; ¹; 4; 0; 1i,
где B = fa; b; c; : : :g – некоторое (конечное или бесконечное) множество элементов, в котором выделены особые элементы 0 и 1. Операции +; ¢; ¹ удовлетворяют аксиомам булевой алгебры (включая законы де Моргана и законы поглощения a + ab = a; a(a + b) = a).
Отношение порядка 4 – нестрогое (рефлексивное, антисимметричное и транзитивное) связано с операциями следующим образом:

2.5. Отношения порядка |
101 |
|
|
|
|
1.a 4 a + b;
2.ab 4 a;
3.b 4 a ) a + b = a; ab = b;
4. b 4 a & c 4 a ) b + c 4 a, a 4 b & a 4 c ) a 4 bc;
5. b 4 a ) b + c 4 a + c; bc 4 ac;
6. a + b = max[a; b], ab = min[a; b] (если a и b сравнимы);
7. b 4 a |
¹ |
|
) a¹ 4 b. |
||
Векторная |
Рассмотрим два m-кортежа |
|
k = ha1; a2; : : : ; ami, |
||
решетка |
l= hb1; b2; : : : ; bmi,
вкоторых ai и bi; i = 1; m принадлежат од-
ному и тому же совершенному порядку (вполне упорядоченному множеству), строгому или нестрогому. Отношение порядка на M обозначим символом >.
Будем говорить, что k доминирует l (k < l) тогда и только тогда, когда
a1 > b1; a2 > b2; : : : ; am > bm.
Для строгого порядка обозначения, соответственно, > и
Â.
В этом случае будем говорить, что k  l (k строго доминирует l), если
a1 > b1; : : : ; ai > bi; : : : ; am > bm,
т.е. имеется по крайней мере один ai и один bi, для которых выполняется строгое соотношение >.
Говорят, что отношение доминирования индуцирует отношение порядка (совершенное или частичное) между кортежами k и l.
Пример 2.36.
k = h7; 3; 0; 5i, l = h2; 2; 0; 4i; p = h3; 4; 1; 4i;
