
- •1. Множества и бинарные отношения
- •Множества
- •Определения и примеры
- •1.1.1 Множество
- •Операции над множествами
- •Элементы комбинаторики
- •Бинарные отношения
- •Определения и примеры
- •2.1.2 Отображения
- •Операции над отношениями
- •Выполнение операций над отношениями
- •Свойства отношений
- •Эквивалентность и толерантность
- •2.4.1 Эквивалентность
- •2.4.3 Толерантность
- •2.4.6 Задача о наименьшем покрытии (ЗНП)
- •Алгоритм решения ЗНР
- •Отношения порядка
- •Строгий порядок
- •Свойства строгого порядка
- •Некоторые свойства дерева
- •Анализ отношений порядка
- •2.5.8 Решетки
- •2.5.10 Решетка
- •2.5.11 Булева решетка
- •Нормированные булевы решетки
- •Модели нормированной булевой решетки
- •Булевы функции (БФ)
- •Определения и примеры
- •Равенство булевых функций
- •3.3.1 СДНФ
- •3.3.3 СКНФ
- •3.3.5 Представление формул в СДНФ и СКНФ
- •Минимизация булевых функций
- •3.4.1 Импликанта
- •Полные системы булевых функций
- •2. Математическая логика
- •Логика высказываний
- •Основные понятия
- •4.1.7 Логическое следствие
- •4.1.8 Теоремы о логическом следствии
- •Логика предикатов
- •5.0.13 Связанные и свободные переменные
- •Предваренная нормальная форма
- •Стандартная нормальная форма
- •Подстановки и унификация
- •Метод резолюций для логики первого порядка
- •Исчисление высказываний
- •3. Графы
- •Определения и примеры
- •Определения графа
- •Части графа
- •Изоморфизм графов
- •Задание графов с помощью матриц
- •Матрица инциденций
- •Матрица соседства вершин
- •Матрица смежности
- •Типы графов
- •Обыкновенные графы
- •Графы Бержа
- •Помеченные и взвешенные графы
- •Другие способы задания графа
- •Связность графов
- •Маршруты, цепи, циклы
- •Число маршрутов
- •Компоненты связности
- •Нахождение компонент и бикомпонент
- •Кратчайшие цепи
- •Алгоритм Форда
- •Алгоритм Дейкстры
- •Обходы графа
- •Поиск в глубину на графе
- •Поиск в ширину на графе
- •Эйлеровы цепи и циклы
- •Эйлеровы пути
- •Гамильтоновы цепи и циклы
- •Цикломатика графов
- •Цикломатическое число
- •Деревья
- •Свойства дерева
- •Каркасы
- •Алгоритм нахождения каркаса графа.
- •Кратчайший каркас графа.
- •Алгоритм Прима.
- •Теорема о хорде каркаса.
- •Число каркасов графа.
- •Разрезы
- •Пространства суграфов
- •Пространство циклов
- •Пространство разрезов.
- •Потоки в сетях
- •Задача о максимальном потоке
- •Постановка задачи
- •Экстремальные части графа
- •Основные понятия
- •Покрытия
- •Задача о наименьшем покрытии
- •Паросочетания
- •Раскраска вершин графа
- •Хроматическое число
- •Оценки хроматического числа
- •Точные алгоритмы раскраски вершин

105
Глава 3
Булевы функции (БФ)
3.1 Определения и примеры
Булевы |
Булевы функции (функции алгебры ло- |
гики) определяются на множестве наборов |
|
функции |
(векторов), состоящих из нулей и единиц, |
|
и принимают значение 0 или 1. |
Определение. Булевы константы 0 и 1 образуют булево множество B = f0; 1g: Булева переменная – переменная, которая может принимать значение из B:
Булева функция (БФ) n переменных – это отображение
f : Bn 7!B:
Булеву функцию можно представить в виде
y= f(x1; x2; : : : ; xn);
вкотором каждая булева переменная xi и функция f могут принимать одно из двух возможных значений 0 или 1: Зна-
чение функции соответствует набору значений переменных ha1 ¢ ¢ ¢ ; ani 2 Bn, где ai есть фиксированное значение пере-
менной xi, ai 2 f0; 1g;
f(a1; ¢ ¢ ¢ ; an):

106 Глава 3. Булевы функции (БФ)
Булев вектор (набор) ha1 ¢ ¢ ¢ ; ani 2 Bn будем изображать в виде последовательности значений булевых переменных (компонент вектора) без скобок и запятых (для сокращения записи) a1a2 ¢ ¢ ¢ an: Длина вектора – число его компонент, а вес вектора – число единиц в нем.
Пример 3.1. Длина вектора ~a = a1a2a3a4a5 = 10101 равна 5, а его вес – 3. J
Теорема 3.1 jBnj = 2n (число различных векторов длины n равно 2n).
До к а з а т е л ь с т в о .
Векторы упорядочены отношением доминирования 4: для
~
векторов ~a = a1 : : : an; b = b1 : : : bn;
|
~ |
|
|
~a 4 b , 8i ai 6 bi (0 < 1): |
|
|
~ |
|
|
Доминирование строгое (~a Á b), если хотя бы для одного |
|
~i |
~ |
~ |
ai < bi. Если для векторов ~a; b не выполняются ни ~a 4 b, ни |
||
b 4 ~a, то векторы несравнимы. |
|
|
Пример 3.2. |
|
|
|
~a = 1011; |
|
|
~ |
|
|
b = 1001; |
|
|
~c = 1101; |
|
~ |
~ |
|
b Á ~a, b Á ~c, ~a и ~c несравнимы. J |
|
|
Векторы разных размерностей нельзя сравнивать по отношению доминирования.
Булев вектор можно рассматривать как двоичное представление целого неотрицательного десятичного числа. Если компоненты вектора ~a = a1 : : : an интерпретировать как числа 0 и 1, то десятичное число a 2 f0; 1; : : : ; 2n ¡ 1g есть
Xn
a = ai ¢ 2n¡i:
i=1
Например, вектор ~a = 1011 представляет число
1 ¢ 23 + 0 ¢ 22 + 1 ¢ 21 + 1 ¢ 20 = 8 + 0 + 2 + 1 = 11:
3.1. Определения и примеры |
107 |
|
|
|
|
В десятичном представлении векторы упорядочены в линейном порядке.
Множество всех булевых функций n переменных обозначим
Pn = ffjf : f0; 1gn 7!0f; 1gg:
Теорема 3.2
jPnj = 22n :
Д о к а з а т е л ь с т в о . Число булевых векторов длины n (число n-кортежей над двухэлементным множеством f0; 1g)
равно 2n. В свою очередь, jPnj есть число 2n-кортежей над f0; 1g, то есть jPnj = 22n :
Булеву функцию можно представить таблицей с 2n строками и n + 1 столбцами. В первых n столбцах перечисляются наборы значений аргументов a1 : : : an в лексикографическом порядке (по возрастанию чисел,
представленных векторами, от 0 до 2n¡1), а в (n+1)-м столбце
– значения функции для этих аргументов.
Таблица 3.1. Табличное представление БФ
|
|
x1 |
¢ ¢ ¢ |
xn |
|
f(x1; : : : ; xn) |
0 |
|
0 |
: : : |
0 |
|
f(0; : : : ; 0) |
1 |
|
0 |
: : : |
1 |
|
f(0; : : : ; 1) |
: : : |
|
: : : |
: : : |
: : : |
|
: : : |
2n ¡ 1 |
|
1 |
: : : |
1 |
|
f(1; : : : ; 1) |
Слева в таблице добавлен столбец с десятичными номерами векторов.
Если интерпретировать элементы множества f0; 1g как истинностные значения "ложь” и "истина” некоторых высказываний, то булеву функцию можно считать некоторым сложным высказыванием. При этом истинностное значение f зависит от истинностных значений переменных.
108 |
Глава 3. Булевы функции (БФ) |
|
|
С другой стороны, булеву функцию можно считать n- арной операцией на множестве f0; 1g. Таким образом, понятие логических операций :; ^; _; !; $ является частным случаем общего понятия логической операции. Таблицу, представляющую булеву функцию, можно считать таблицей истинности этой операции.
Примеры 3.3. 1. При n = 0 булевых функций две (220 = 21): константа 0 и константа 1.
2. Булевы функции одной переменной.
При n = 1 число булевых функций равно 4 (221 = 22):
Таблица 3.2. Булевы функции одной переменной |
|||||||
|
|
|
|
|
|
|
|
|
x |
|
f0(x) |
f1(x) |
f2(x) |
f3(x) |
|
|
0 |
|
0 |
0 |
1 |
1 |
|
|
1 |
|
0 |
1 |
0 |
1 |
|
Здесь в одной таблице представлены четыре функции одной переменной. Они имеют собственные названия:
f0(x) – 0, нуль;
f1(x) – тождественная функция;
f2(x) – : x,отрицание, инверсия (другие обозначения: x;¹ » x);
f3(x) – 1, единица.
3. Булевы функции двух переменных.
При n = 2 число булевых функций равно 16 (222 = 24):
Таблица 3.3. Булевы функции двух переменных
x1 |
x2 |
|
f0 |
f1 |
f2 |
f3 |
f4 |
f5 |
f6 |
f7 |
f8 |
f9 |
f10 |
f11 |
f12 |
f13 |
f14 |
f15 |
0 |
0 |
|
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
0 |
1 |
|
0 |
0 |
0 |
0 |
1 |
1 |
1 |
1 |
0 |
0 |
0 |
0 |
1 |
1 |
1 |
1 |
1 |
0 |
|
0 |
0 |
1 |
1 |
0 |
0 |
1 |
1 |
0 |
0 |
1 |
1 |
0 |
0 |
1 |
1 |
1 |
1 |
|
0 |
1 |
0 |
1 |
0 |
1 |
0 |
1 |
0 |
1 |
0 |
1 |
0 |
1 |
0 |
1 |
Обозначения и названия некоторых функций двух переменных:
f0 – 0, нуль;
f1 – x1 ^ x2, конъюнкция (другие обозначения: &; ¢);
f6 – x1 © x2, исключающее "или”, сложение по модулю 2; f7 – x1 _ x2, дизъюнкция, ( другое обозначение +);
f8 – x1 # x2, стрелка Пирса;
3.1. Определения и примеры |
109 |
|
|
|
|
f9 – x1 $ x2, эквиваленция (другие обозначения: »; ´); f13 – x1 ! x2, импликация (другие обозначения: ¾; )); f14 – x1jx2, штрих Шеффера;
f15 – 1, единица.
4. Мажоритарная функция (функция голосования, принимает значение 1, если "за” проголосовало большинство).
Таблица 3.4. Мажоритарная функция
|
|
x1 |
x2 |
x3 |
|
f(x1; x2; x3) |
0 |
|
0 |
0 |
0 |
|
0 |
1 |
|
0 |
0 |
1 |
|
0 |
2 |
|
0 |
1 |
0 |
|
0 |
3 |
|
0 |
1 |
1 |
|
1 |
4 |
|
1 |
0 |
0 |
|
0 |
5 |
|
1 |
0 |
1 |
|
1 |
6 |
|
1 |
1 |
0 |
|
1 |
7 |
|
1 |
1 |
1 |
|
1 |
|
|
|
|
|
|
|
Булевы функции с числом переменных n 6 2 называются
элементарными.
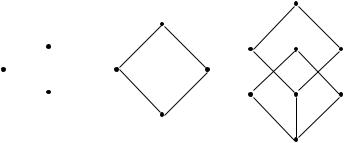
Область определения БФ n переменных множество Bn = f0; 1gn можно интерпретировать геометрически как булев n-мерный куб (гиперкуб). Вершинами гиперкуба являются n-мерные булевы векторы, упоря-
доченные отношением доминирования. Гиперкуб, как упорядоченное множество, можно представить с помощью диаграммы Хассе. Булевой функции ставится в соответствие то подмножество A µ Bn вершин куба, на которых функция равна 1:
fA(x1 |
; : : : ; xn) = |
1; |
fx1; : : : ; xng 2 A |
|
½ |
0; |
в противном случае |
Пример 3.4.
110 |
|
|
Глава 3. Булевы функции (БФ) |
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
111 |
|
|
||
|
1 |
11 |
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
011 |
|
|
|
|
110 |
||
|
|
|
|
101 |
|
|||
|
|
|
|
|
||||
0; 1 |
|
01 |
10 |
|
|
|
||
|
|
|
|
|
|
|
|
|
n = 0 |
0 |
001 |
|
010 |
|
100 |
||
|
n = 1 |
00 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
n = 2 |
000 |
|
|
||
|
|
|
|
|
n = 3 |
|
|
|
Рис. 3.1. Булевы гиперкубы.
Мажоритарной функции соответствует множество
f011; 101; 110; 111g на трехмерном кубе, сложению по модулю 2 – множество f01; 10g на двухмерном кубе. Функции 0 соответствует пустое множество ?, а функции 1 – множество всех вершин гиперкуба Bn: J
Представление вектором значений. Так как множество векторов упорядочено от 0 до 2n ¡ 1, то для представления функции достаточно задать значения функции в этом порядке.
Пример 3.5. Мажоритарная функция трех переменных задается вектором 00010111, сложение по модулю 2 (функция двух переменных) – вектором 0110.
Можно также перечислить десятичные номера тех векторов, на которых булева функция принимает значение 1: Для мажоритарной функции трех переменных f = f3; 5; 6; 7g; для сложения по модулю 2 (функции двух переменных) – f = f1; 2g: J
Представление Определение. Суперпозицией булевых
БФ формулами функций f0 и f1; : : : ; fm называется функция
f(x1; : : : ; xn) = f0(f1(x1; : : : ; xn); : : : ; fm(x1; : : : ; xn)):
Выберем некоторое подмножество функций n переменных x1; : : : ; xn
3.1. Определения и примеры |
111 |
|
|
|
|
© = ff1; : : : ; fmg; |
© µ Pn; |
|
Pn = ff(x1; : : : ; xn)jf : f0; 1gn 7!0f; 1gg:
Множество © называется базисом.
Определение. Формулой над базисом © = ff1; : : : ; fmg называется суперпозиция F = f(f1; : : : ; fm); где f 2 ©:
f называется главной (внешней) функцией (операцией), а fi – подформулой. Всякой формуле F однозначно соответствует некоторая булева функция f: Говорят, что формула F реализует функцию f и обозначают Ff .
Формулы над множеством элементарных функций называют просто формулами.
Пример 3.6. Рассмотрим базис © = f ¹ ; ^; _g. Это множество, состоящее из отрицания, конъюнкции и дизъюнкции называется стандартным базисом. Формулой над стандартным базисом будет любая переменная x; y; x1; x2; : : : ; xn: Далее, из переменных x; y можно построить новую формулу _(x; y) или ^(x; y). Для записи этих формул чаще используют инфиксную нотацию (x _ y); (x ^ y). Отрицание записывают в виде (¹x), а не¹(x).
В формулах над стандартным базисом используют ассоциативность операций ^ и _, используют соглашение о приоритете операций ( ¹; ^; _) и опускают внешние скобки. Например, вместо (¹(x _y) _((y ^z) ^v) записывают (x _ y) _y ^z ^v. Знак конъюнкции часто заменяют на ¢ или вовсе опускают, знак дизъюнкции заменяют на +. Тогда наша формула примет вид (x + y) + yzv. Порядок выполнения операций определяется приоритетом операций и расстановкой скобок.
Построим таблицу для функции f, которую реализует формула x¹ + xy + xy¹ .
x |
y |
|
f |
|
|
|
|
0 |
0 |
|
1 |
0 |
1 |
|
1 |
1 |
0 |
|
0 |
1 |
1 |
|
1 |
|
|
|
|
Полученная функция есть ни что иное как f13 из таблицы функций двух переменных – импликация. J
