
- •§9. Метрические пространства
- •Положим в (3) . Тогда
- •Примеры метрических пространств
- •§10. Геометрия метрического пространства Окрестность точки. Предельная точка множества
- •Внутренность, замыкание и граница множества
- •Открытые и замкнутые множества
- •Свойства открытых и замкнутых множеств
- •Некоторая дополнительная терминология
- •§11. Предел последовательности в метрическом пространстве Сходящиеся последовательности
- •Сходимость в пространствах RnиC[a,b]
- •1. Пространство Rn
- •2. Пространство c[a,b]
- •Фундаментальные последовательности
- •Полные метрические пространства
- •Примеры полных метрических пространств
- •§12. Линейные нормированные пространства Пусть множество, в котором:
- •§13. Гильбертовы пространства
- •Примеры предгильбертовых и гильбертовых пространств
Примеры полных метрических пространств
1. Пространство R полно.
Это следует
из критерия Коши сходимости числовой
последовательности: последовательность
![]() сходится тогда и только тогда, когда
она фундаментальная.
сходится тогда и только тогда, когда
она фундаментальная.
2. Пространство Rп полное пространство.
Это следует из полноты пространства R.
Пусть
![]() фундаментальная последовательность
точек пространстваRп,
то есть
фундаментальная последовательность
точек пространстваRп,
то есть
![]() .
.
Тогда
![]()
![]() .
.
Здесь
![]() .
Тогда
.
Тогда![]() тем более будут выполняться неравенства
тем более будут выполняться неравенства
![]()
![]() .
.
Это означает,
что последовательности
![]() ,
,![]() ,
- фундаментальные. Но тогда (из примера
1) они являются сходящимися, то есть
существуют пределы:
,
- фундаментальные. Но тогда (из примера
1) они являются сходящимися, то есть
существуют пределы:![]() ,
,![]() .
Пусть
.
Пусть![]() .
Очевидно:
.
Очевидно:
1.
![]() Rп,
Rп,
2.
![]() (так как сходимость последовательности
точек пространстваRnпонимается как сходимость по координатам).
(так как сходимость последовательности
точек пространстваRnпонимается как сходимость по координатам).
Таким образом доказано, что пространство Rnполно.
3. Пространство C[a,b] полно.
Сходимость последовательности точек пространства C[a,b]есть равномерная сходимость последовательности непрерывных функций. Пределом такой последовательности является непрерывная функция, то есть элемент пространстваC[a,b],что и требовалось доказать.
4. Пространство т полно.
5. Пространство
![]() полно.
полно.
§12. Линейные нормированные пространства Пусть множество, в котором:
1. введена операция, ставящая в соответствие
каждой паре элементов
![]() элемент из,
называемый суммой этих элементов и
обозначаемый
элемент из,
называемый суммой этих элементов и
обозначаемый![]() ,
причем выполнены следующие аксиомы:
,
причем выполнены следующие аксиомы:
1)
![]() (коммутативность сложения);
(коммутативность сложения);
2)
![]() (ассоциативность сложения);
(ассоциативность сложения);
3) существует
единственный элемент
![]() ,
называемый нулевым элементом или нулем,
такой, что
,
называемый нулевым элементом или нулем,
такой, что![]() ;
;
4) каждому
элементу
![]() соответствует единственный противоположный
элемент из,
обозначаемый
соответствует единственный противоположный
элемент из,
обозначаемый![]() ,
такой, что
,
такой, что![]() .
.
2. введена операция умножения элементов из на число изR (C), удовлетворяющая следующим аксиомам:
5)
![]() (ассоциативность умножения);
(ассоциативность умножения);
6)
![]() (дистрибутивность умножения);
(дистрибутивность умножения);
7)
![]() (дистрибутивность умножения);
(дистрибутивность умножения);
8)
![]() .
.
Определение 1.Множествос операциями 1 и 2, удовлетворяющими аксиомам 1-8 называетсялинейным пространством над полем R (C).
Определение 2.Линейное пространствонад полемRназываетсянормированным,если каждому элементу![]() поставлено в соответствие действительное
число, называемоенормойэлемента
поставлено в соответствие действительное
число, называемоенормойэлемента![]() и обозначаемое
и обозначаемое![]() ,
удовлетворяющее следующимаксиомам
нормы:
,
удовлетворяющее следующимаксиомам
нормы:
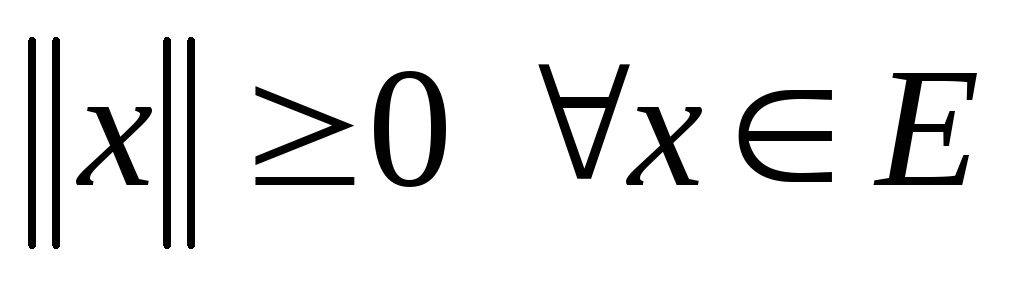 ,
причем
,
причем ;
;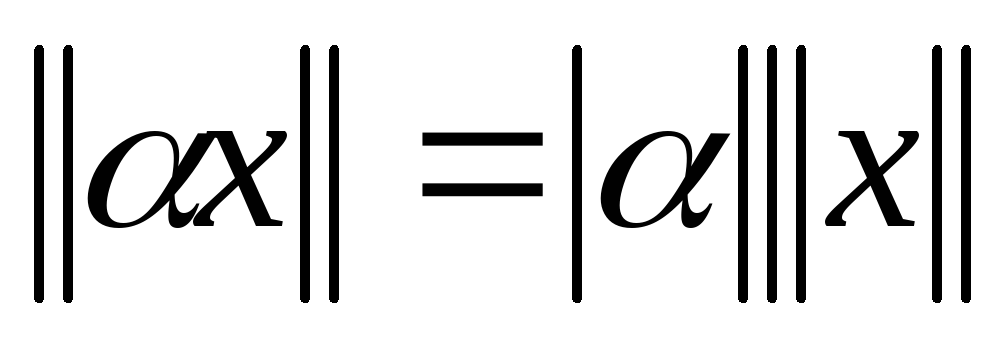
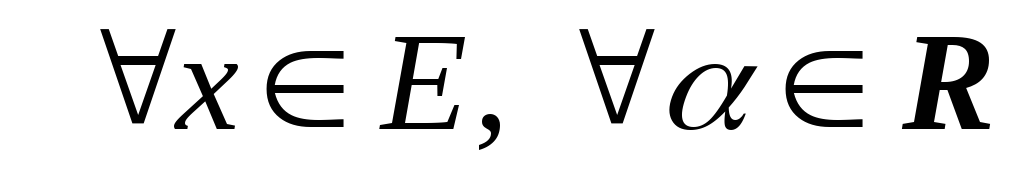 ;
;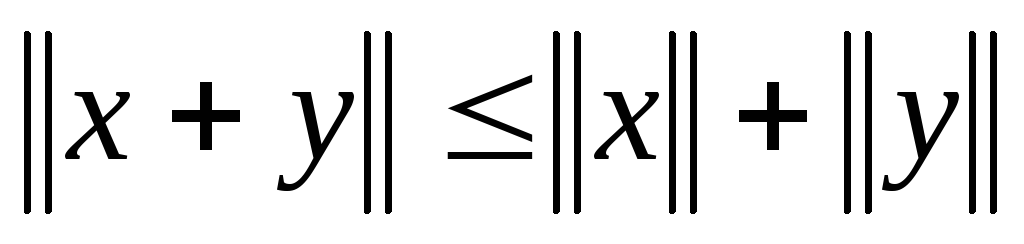
 .
.
Теорема.Всякое нормированное пространство
является метрическим с метрикой![]() .
.
Доказательство:
Пусть нормированное
пространство. Докажем, что функция![]() задает метрику на.
Для этого проверим справедливость
аксиом 1-3 метрического пространства:
задает метрику на.
Для этого проверим справедливость
аксиом 1-3 метрического пространства:
1.
![]() ;
;
![]() .
.
2.
![]() ;
;
![]()
![]() =
=![]() =
=![]() =
=![]()
![]() .
.
3.
![]() ;
;
![]()
![]() =
=![]()
![]() .
.
На нормированные пространства переносятся многие понятия и их свойства, справедливые для метрических пространств, в частности, имеется понятие сходимости последовательности.
Определение
3. Последовательность![]() ,
называетсясходящейся
к x,если
,
называетсясходящейся
к x,если
![]() .
.
Определение
4.Последовательность![]() называетсяфундаментальной,если
называетсяфундаментальной,если
![]()
Определение 5. Нормированное пространствоназываетсяполным, если любая фундаментальная последовательность его точек сходится к точке этого же пространства. Полное нормированное пространство называетсябанаховым пространством.
Пример.
Пространство
![]() - банахово пространство.
- банахово пространство.
1. Определим операции IиIIобычным способом:
![]() ,
,
![]() .
.
Очевидно выполнение аксиом 1-8 линейного пространства.
Введём норму:
![]() .
.
Проверим выполнение аксиом нормы.
![]() :
:
1.
![]() ,
,![]()
![]()
![]() .
.
2.
![]() .
.
3.
![]()
![]()
![]()
![]() .
.
Таким образом,
![]() - нормированное пространство.
- нормированное пространство.
Далее, так
как
![]() - полное метрическое пространство, то
- полное метрическое пространство, то![]() - полное метрическое пространство,
следовательно,
- полное метрическое пространство,
следовательно,![]() - банахово пространство.
- банахово пространство.
