Сходимость в пространствах RnиC[a,b]

1. Пространство Rn

Пусть дана последовательность точек

. (1)

Задание последовательности (1) равносильно заданию ппоследовательностей:

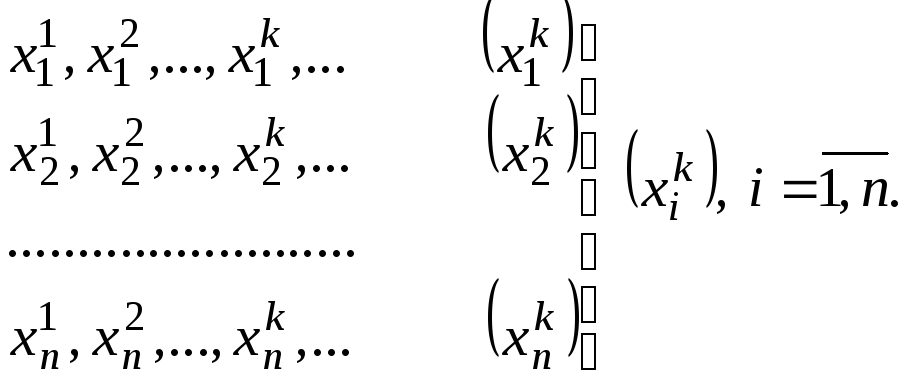
Переформулируем определение 1 для нашего случая:

Определение 5.Точканазываетсяпределом последовательности (х_к), где, если числовая последовательностьсходится к нулю.

Теорема 5.Последовательность точек, сходится к точкетогда и только тогда, когда последовательности компонент, сходятся соответственно к компонентам.

Доказательство:

Справедливы неравенства:

.

Действительно,

а) ;

;

б) Возведём в квадрат обе части неравенства:

- верно.

1. Необходимость.

Пусть . Докажем, что.

По определению

.

Далее имеем:

.

2. Достаточность.

Пусть . Докажем, что.

Возьмём . По определению

.

Положим . Тогда:

.

Из теоремы 5 следует, что сходимость по метрике пространства Rⁿ равносильна покоординатной (поточечной) сходимости.

2. Пространство c[a,b]

Пусть дана последовательность пространства,. Пусть далее,. По определению

-

определение равномерной сходимости функциональной последовательности к функциина отрезке. Таким образом,сходимость по метрике пространства C[a,b] равносильна равномерной сходимости на [a,b].

Фундаментальные последовательности

Пусть М– метрическое пространство с метрикой,.

Определение 6.Последовательность точек, называетсяфундаментальной, если

.

Пусть (если, то). Ясно, что если, то. Следовательно, выполняется неравенствои имеет место определение:

Определение 7.Последовательность точек, называетсяфундаментальной, если

.

Теорема 6.ПустьМ– метрическое пространство,. Если, - фундаментальная последовательность в одном из пространствМилиЕ, то она будет фундаментальной и в другом пространстве.

Доказательство:

Заметим, что

. (1)

1. Пусть , - фундаментальная последовательность в пространствеЕ, тогда по определению

. (2)

Так как и, то. Тогда из (1) и (2) следует, что

.

По определению последовательность фундаментальна вМ.

2. Пусть - фундаментальная последовательность в пространствеМ, нои верно равенство (1). Следовательно,фундаментальна вЕ.

Теорема 7. Всякая фундаментальная последовательность ограничена.

Доказательство:

Пусть М– метрическое пространство,- фундаментальная последовательность вМ.Тогда по определению для любого, в том числе для

.

В качестве числа возьмём(зафиксировали). Тогда

.

Обозначим

.

Тогда

.

По определению последовательность ограничена.

Теорема 8. Всякая сходящаяся последовательность фундаментальна.

Доказательство:

Пусть

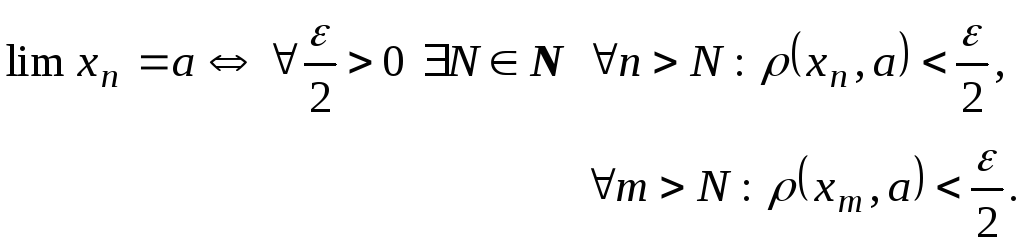
Тогда в силу неравенства треугольника

.

По определению последовательность фундаментальна.

Полные метрические пространства

В связи с теоремой 8 отметим, что не всякая фундаментальная последовательность элементов метрического пространстваявляется сходящейся последовательностью в данном пространстве.

Пример 1.Рассмотрим метрическое пространство=(0,1)с метрикой. Возьмём последовательность. Тогда

при.

По определению последовательность фундаментальная, но она не сходится ни к какому элементу пространстваМ, то есть в пространстве сходящейся не является.

Пример 2.Пустьпространство многочленов с действительными коэффициентами

,

определённых на отрезке с метрикой

.

Возьмем последовательность многочленов , где

, .

Пусть . Оценим :

при . Итак, по определению последовательностьфундаментальная. Решим вопрос её сходимости:

,

то есть последовательность не сходится в пространстве многочленов.

В связи с примерами 1 и 2 дадим определение:

Определение 8.Метрическое пространство называетсяполным, если в нем всякая фундаментальная последовательность сходится к некоторому пределу, являющемуся элементом этого пространства.