§9. Метрические пространства

В математическом анализе важнейшую роль играет понятие предела. В основе различных определений предела лежит то или иное понятие близости между объектами. Поэтому естественно попытаться для множеств произвольной природы ввести понятие расстояния между элементами, а затем и понятие предельного перехода.

Определение 1. На множестве Х определена структура метрического пространства, если задана функция пары аргументов

,

обладающая свойствами:

1. ;

2. ;

3. (неравенство треугольника).

Функция ,,называется метрикой или функцией расстояния, число называетсярасстоянием между точками и.

Итак, метрическое пространство образует пара: множество Х и функция . Обозначается:или. Если в условиях конкретной задачи ясно, о какой метрике идёт речь, то метрическое пространство обозначаютХ или М.

Свойство 1..

Доказательство:

Положим в (3) . Тогда

.

Примеры метрических пространств

1. а) Арифметическое п-мерное пространствоХ, точки которого – упорядоченные наборыпдействительных чисел,, - метрическое пространство с метрикой

.

В дальнейшем эту пару будем обозначать.

б) X– то же,.- метрическое пространство.

в) X– то же,.- метрическое пространство.

г) X– то же,.- метрическое пространство.

д) X– то же, - метрическое пространство.

е) X– то же, - метрическое пространство.

2. Пусть Y– множество непрерывных функций, заданных на отрезке . Введём метрики следующим образом:

а) ,- метрическое пространство. Обозначается.

б) можно ввести по правилам б), д), е) примера 1.

в) ,- метрическое пространство.

г) 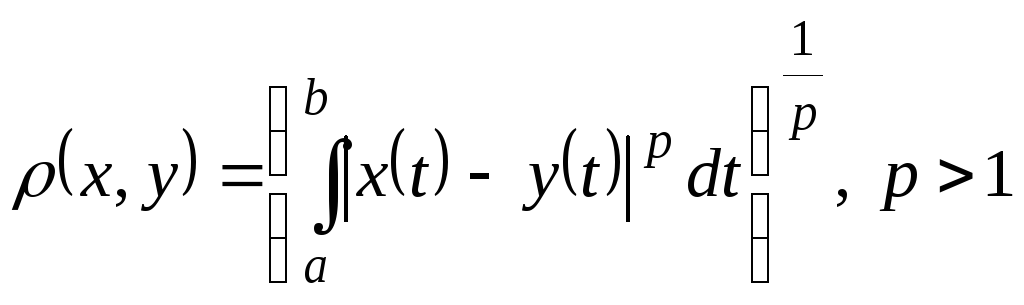,- метрическое пространство.

3. Пусть Z– множествопраз непрерывно-дифференцируемых функций на отрезке ,.- метрическое пространство с метрикой

.

Обозначается .

4. Пусть U– множество, состоящее из последовательностей действительных чиселтаких, что

.

а) Введём метрику по правилу:

.

- метрическое пространство. Обозначается- бесконечномерное евклидово пространство.

б) .- метрическое пространство.

5. Пусть V- множество последовательностей действительных чиселтаких, что

.

Определим функцию расстояния по формуле

.

- метрическое пространство. Обозначается.

6. Пусть W- множество последовательностей действительных чиселтаких, что

.

Определим функцию расстояния по формуле

.

- метрическое пространство. Обозначается.

Упражнение.Проверить, что пространства примеров 1, 2а, 2б, 2в, 3, 4б, 6 являются метрическими пространствами.

Пример.Проверим, что пространство- метрическое пространство (пример 4а), для этого покажем, что функция

определена для любых и удовлетворяет условиям 1-3 определения метрического пространства.

Возьмём ,,, такие, что

,,.

Справедливо неравенство:

,

(действительно, ,

,

).

Так как ряды исходятся, то сходится ряд. Следовательно, по признаку сравнения сходимости положительных рядов сходится ряд, то есть функцияопределена.

Проверим выполнимость аксиом 1-3 метрического пространства:

1. ;

.

2. ;

.

3. ;

В аксиома 3 имеет вид:

.

На основании доказанного выше все ряды в последнем неравенстве сходятся. Докажем само неравенство. Имеем:

(см. пример 1а). Переходя в этом неравенстве к пределу при , получим нужное неравенство.