Доказательство.

Будем обозначать пересечение множеств ,,... символом. В силу тождествадоказываемая теорема сразу вытекает из теорем 2 и 4.

Теорема 6. Разность двух измеримых множеств является измеримым множеством.

Доказательство вытекает из тождества и из теорем 4 и 5.

Переходим теперь к доказательству основной теоремы теории меры.

Теорема 7. Мера суммы конечного или счетного числа попарно измеримых непересекающихся множеств равна сумме мер этих множеств.

Доказательство.

Пусть , причем множестваизмеримы и попарно не пересекаются. Рассмотрим отдельно два случая.

1) Сначала предположим, что все ограничены. Заметим, что для случая, когда всезамкнуты и их конечное число, доказываемая теорема сразу вытекает из свойств внешней меры.

Пусть теперь - произвольные ограниченные попарно не пересекающиеся множества.

В силу следствия из теоремы 4 для любого и для каждого номеранайдется замкнутое множество, содержащееся ви такое, что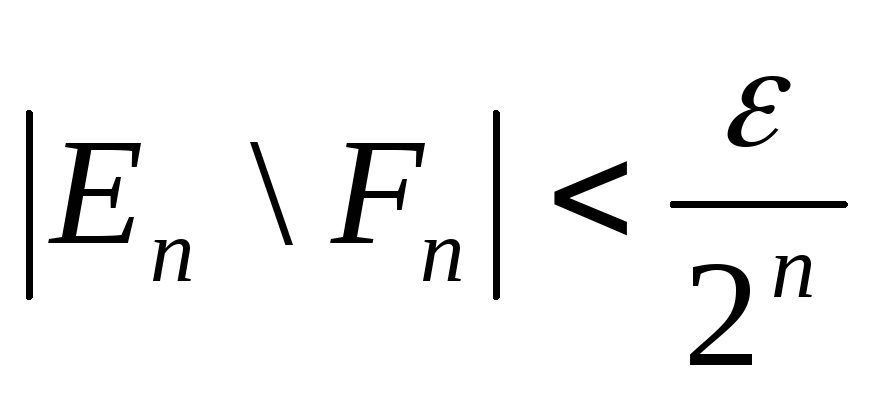. Так как все множестваограничены, замкнуты и попарно не пересекаются, то для любого конечногов силу сделанного выше замечания

(10)

С другой стороны, из равенства вытекает (в силу свойств внешней меры), что,

так что

(11)

(для любого конечного ). Из (10) и (11) заключаем, что для любого конечного

(12)

Учтем теперь, что сумма всех множеств содержится в. Отсюда следует, что для любого номера

,

так что (в силу (12)) для любого номера

(13)

Переходя в (8.15) к пределу при , мы получим, что

,

и, стало быть, на основании произвольности

. (14)

Теперь остается заметить, что из равенства суммы множествуи из свойств внешней меры вытекает обратное неравенство

. (15)

Из неравенств (14) и (15) вытекает утверждение доказываемой теоремы (для случая ограниченных множеств ).

2) Пусть теперь множества не являются, вообще говоря, ограниченными. Тогда мы обозначим символомограниченное множество.

Из равенства и из рассмотренного выше случая следует, что

.

Теорема полностью доказана.

Для того чтобы сформулировать еще одно свойство меры, введем новое понятие.

Определение 2. Назовем множество множеством типа, еслипредставимо в виде пресечения счетного числа открытых множеств, и множеством типа, еслипредставимо в виде суммы счетного числа замкнутых множеств.

Теорема 8. Если множество измеримо, то найдутся множествотипа, содержащееся в, и множествотипа, содержащее, для которых.

Доказательство.

В силу измеримости и следствия из теоремы 8.5 для любого номеранайдутся открытое множество, содержащее, и замкнутое множество, содержащееся в, такие, что

, . (16)

Положим ,. Так как для любого номера

, ,

то в силу (16) и свойства 1’ внешней меры

, .

В силу произвольности номера отсюда следует, чтои. Теорема доказана.