Доказательство.

Проведем доказательство в два шага.

1) Сначала предположим, что множество ограничено. Фиксируем произвольное. Согласно свойствам внешней меры (пересечение любого конечного числа открытых множеств является открытым множеством) найдется открытое множество, содержащееи такое, что

(2)

Известно что, если множество замкнуто, а множествооткрыто, то множествозамкнуто, а множествооткрыто, множество

является открытым. Поэтому, согласно множество представимо в виде суммыпопарно не пересекающихся интервалов. Теорема будет доказана, если мы установим, что

. (3)

Для каждого интервала и для каждого числаиз интерваладоговоримся обозначать символоминтервал, а символомсегмент. Если же, тобудет обозначать пустое множество, для которого. Для каждого номераположим. Очевидно, что. Множество, согласно свойству 6’(сумма конечного числа замкнутых множеств является замкнутым множеством), является замкнутым. Так как это множество не имеет общих точек с замкнутым множеством, то в силу свойств внешней меры (сумма любого числа открытых множеств является открытым множеством)

. (4)

С другой стороны, поскольку множество (при любоми для всех номеров) содержится в, то в силу свойств внешней меры (если множествозамкнуто, то его дополнениеоткрыто)

(5)

Из (2), (4) и (5) получим, что

(6)

(для всех и всех номеров). Так как множествоограничено и его внешняя мера, из (6) получим, что

(7)

(для всех и всех номеров). Переходя в (7) к пределу сначала при, а затем при, мы получим неравенство (3). Тем самым для случая ограниченного множестватеорема доказана.

2) Если замкнутое множество , вообще говоря, не является ограниченным, то мы представимв виде суммы, где- пересечение замкнутых множестви. Согласно доказанному в первом шаге каждоеизмеримо (ибо оно замкнуто и ограничено), а поэтому измеримо и множество. Теорема полностью доказана.

Теорема 4. Если множество измеримо, то и его дополнениеизмеримо.

Доказательство.

По определению измеримости множества для любого номеранайдется содержащееоткрытое множество, для которого

. (8)

Пусть . Посколькудля любых множеств

и , тои, стало быть,. Из последнего равенства следует, что для любого номера

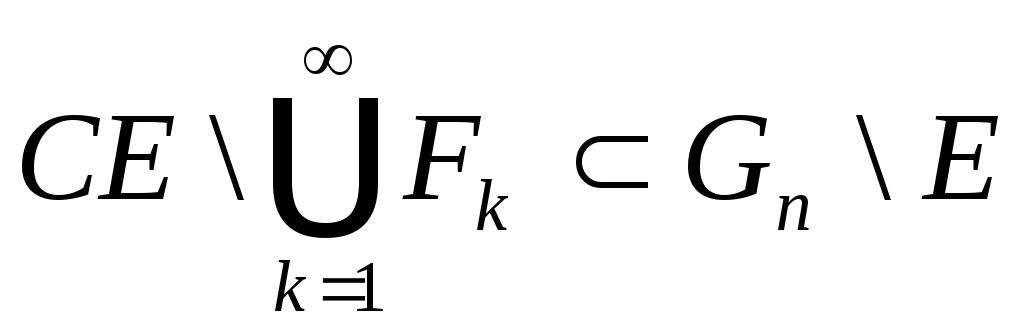(9)

(Запись означает, чтопринадлежит.)

Из (9) и из свойств внешней меры получим, что для любого номера

,

а из последнего неравенства и из (8.10) получим, что

(для любого номера ). Но это означает, что внешняя мера, а стало быть, и мера множестваравна нулю, т.е. множествои. Следовательно,измеримо. Теорема доказана.

Следствие. Для того чтобы множество было измеримо, необходимо и достаточно, чтобы для любого положительного числанашлось замкнутое множество, содержащееся ви такое, что внешняя мера разности

меньше .

Доказательство.

Измеримость множества эквивалентна измеримости(теорема 4), т.е. эквивалентна требованию, чтобы для любогонашлось открытое множество, содержащееи такое, что. Но указанное требование (в силу тождества) эквивалентна требованию, чтобы для любогонашлось замкнутое множество, содержащееся ви такое, что. Следствие доказано.

Теорема 5. Пересечение конечного или счетного числа измеримых множеств является измеримым множеством.