
Finansovaya_matematika_v_Excel_Levin_L_A
.pdf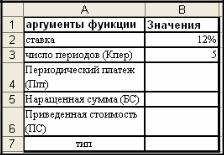
71
3.3.8.Расчет суммы основных платежей по займу. Функция ОБЩДОХОД()
Функция позволяет вычислить сумму основных платежей по займу, который погашается равными платежами в конце или начале каждого расчетного периода, между двумя периодами.
Пример 3-12
Выдана ссуда в размере 1000 тыс. руб. сроком на 6 лет под 15% годовых, начисляемых ежеквартально. Определить величину основных выплат за 5-й год.
Решение
Периоды платежей за 5-й год будут иметь номера 17 и 20, соответственно. Так как ссуда погашается равными платежами в конце каждого периода (квартала), то размер выплаты за пятый год составит:
=ОБЩДОХОД(15%/4;6*4;1000;17;20;0)=201,43 тыс. руб.
3.3.9. Использование операции «Подбор параметра» для определения отдельных параметров аннуитета
Достаточно часто при разработке условий финансовой операции могут возникать ситуации, когда известной величиной является либо наращенная либо приведенная сумма и неполный набор параметров ренты, таких как срок ренты, ставка процента, размер отдельного платежа и др. В таких случаях необходимо найти недостающий параметр., преобразуя соответствующим образом формулы.
При работе в электронной таблице Excel эти величины могут быть легко найдены с помощью операции «Подбор параметра» (команда СЕРВИС ПОДБОР ПАРАМЕТРА).
Пример 3-13
Для покупки автомобиля через 5 лет потребуется 250 тыс. руб. Определите размер взносов, вносимых в конце каждого месяца в банк, который начисляет проценты по ставке 12%.
Решение.
Разместим исходные данные задачи в таблице подобной приведенной на рисунке.
Рис. 3-21 Таблица Excel с исходными данными примера
Постановка задачи требует определить величину ежемесячных платежей, которая позволит за пять лет получить наращенную сумму 250000 руб.
Для решения задачи используем финансовую функцию БС(), разместив ее в ячейке В5.

72
Рис. 3-22 Диалоговое окно функции
БС()
В строке «Ставка» делается ссылка на ячейку (В2), содержащую значение годовой процентной ставки и делится на 12 (число периодов начисления).
В строке «Кпер» делается ссылка на ячейку (В3), содержащую значение количества лет наращения и умножается на 12 (для расчета общего количества начислений за период наращения необходимой суммы).
В строке «Плт» делается ссылка на ячейку (В4), которая будет содержать значение необходимой суммы ежемесячного платежа, которое будет получено после выполнения операции «Подбор параметра».
В строку «Пс» заносится сумма, которая первоначально может быть внесена в банк ( в нашей задаче эта величина равна нулю).
В строке «Тип» записываем «0», так как начисление процентов производится в конце каждого периода.
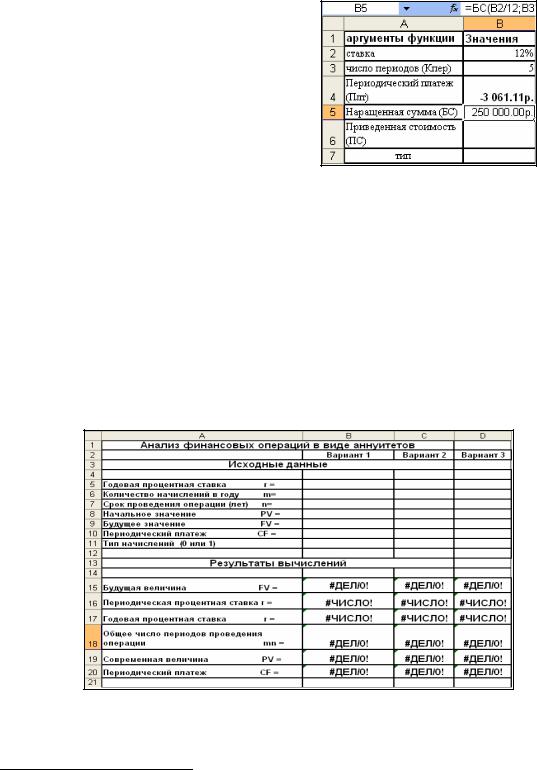
После щелчка на кнопке «Ок» исходная таблица приобретет вид, подобный, показанному на рисунке.
Рис. 3-23 Таблица исходных данных с записанной в ячейку В5 финансовой функцией БС()
Для расчета необходимой величины ежемесячного платежа:
курсор устанавливается в ячейку В5;
выполняется команда СЕВИС ПОДБОР ПАРАМЕТРА.
Рис. 3-24 Диалоговое окно «Подбор параметра»
В открывшемся диалоговом окне команды:
В строке «Установить в ячейке» делается ссылка на ячейку «В5» (величина наращенной суммы, необходимой для приобретения автомобиля);
В строке «Значение» записывается необходимое значение, которая эта ячейка должна получить после выполнения операции «Подбор параметра» ( нашей задаче
– 250000);
73
В строке «Изменяя значение ячейки» делается ссылка на ячейку «В4», значение которой должно быть подобрано для получения необходимой наращенной суммы.
После щелчка на кнопке «ОК» в ячейке В4 будет найдена необходимая величина ежемесячного платежа, который за 5 лет позволит накопить сумму, необходимую для приобретения автомобиля.
Рис. 3-25 Таблица исходных данных с найденной величиной ежемесячного платежа (ячейка В4)
В состав финансовых функций Excel входят функции, необходимые для расчета отсутствующих
параметров38 – функции: ПЛТ()39; «СТАВКА()»; КПЕР() и др.
3.4.РАЗРАБОТКА ШАБЛОНА ДЛЯ АНАЛИЗА АННУИТЕТОВ
Одним из достоинств электронных таблиц является то, что они позволяют создать собственные шаблоны, позволяющие подставляя в них исходные данные немедленно получать необходимые результаты анализа.
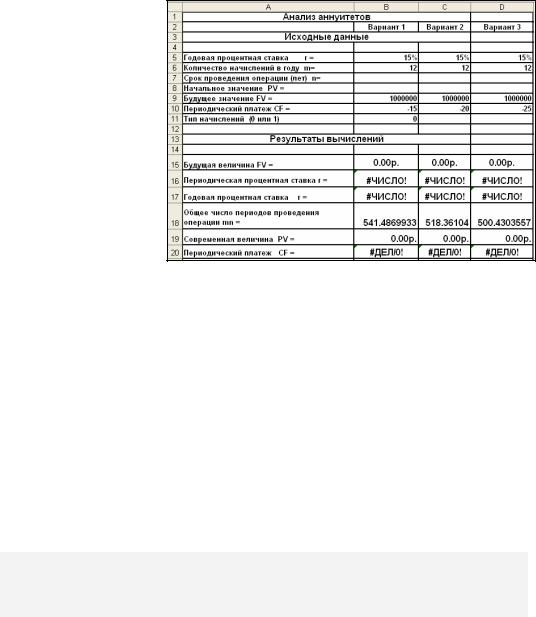
На рис. 3-26 приведен простейший пример шаблона, позволяющий решать типовые задачи по исчислению параметров финансовых операций с элементарными потоками платежей. На рис. 3-27 этот шаблон приведен в режиме отображения формул. Дадим необходимые пояснения.
Рис. 3-26 Шаблон для анализа аннуиетов
38Часть этих функций была нами рассмотрена в главе «ИЗМЕНЕНИЕ СТОИМОСТИ ВЛОЖЕНИЙ ЗА СЧЕТ ПРИСОЕДИНЕНИЯ ПРОЦЕНТОВ»
39В младших версиях Excel эта функция обозначена как ППЛАТ()

74
Рис. 3-27 Шаблон для анализа аннуиетов в режиме отображения формул
|
|
|
Таблица 3-1 |
|
|
Формулы шаблона |
|
|
Ячейка |
|
Формула |
|
|
||
|
|
|
|
|
|
|
|
|
В15 |
|
=БС(B5/B6;B7*B6;B10;B8;B11) |
|
|
|
|
|
В16 |
|
=СТАВКА(B7*B6;B10;B8;B9;B11) |
|
|
|
|
|
В17 |
|
=B16*B6 |
|
|
|
|
|
B18 |
|
=КПЕР(B5/B6;B10;B8;B9;B11) |
|
|
|
|
|
|
|
|
|
В19 |
|
=ПС(B5/B6;B7*B6;B10;B9;B11) |
|
|
|
|
|
В20 |
|
=ПЛТ(B5/B6;B7*B6;B8;B9;B11) |
|
|
|
|
|
|
|
|
Шаблон состоит из двух частей.
Первая часть занимает блок ячеек А5:В11 и предназначена для ввода исходных данных (известных параметров финансовой операции). Текстовая информация в ячейках А5:А11 содержит наименование исходных параметров финансовой операции, ввод которых осуществляется в ячейки B5:B11.
Вторая часть таблицы занимает блок ячеек А15:В20 и предназначена для вывода результатов вычислений, т.е. искомых величин. Блок ячеек В15.В20 содержит формулы, необходимые для вычисления соответствующих параметров финансовой операции и при отсутствии исходных данных содержит сообщения об ошибках:
#Дел/0! – ошибка возникает при делении числа на 0 (нуль); #Число! – ошибка возникает при неправильных числовых значениях в формуле или
функции;
Разработанная таблица-шаблон позволяет быстро и эффективно проводить анализ финансовых операций с элементарными потоками платежей. Так при изменении любой характеристики рассмотренной выше операции, достаточно ввести новое значение в соответствующую ячейку электронной таблицы. Кроме того, шаблон может быть легко преобразован для одновременного анализа сразу нескольких однотипных ситуаций. С этой
целью блоки ячеек В5:В11 и В15:В20 скопированы в блоки ячеек С5:D11 и C15:D120, соответственно.
Сохраните разработанный Вами шаблон на магнитном диске под уникальным именем, например ANNUIT.XLT.
75
Проверим работоспособность шаблона на решении задачи «Как стать миллионером? (пример 4-7).
Пример 3-14
Проанализируем через, сколько лет Вы сможете стать миллионером, если будете ежемесячно вносить в банк 15, 20 или 25 долларов США.
В ячейки шаблона введем исходные данные. Полученная в итоге таблица будет иметь вид, показанный на рис.3-28
Рис. 3-28 Решение примера 3-14
Таким образом, если Вы будете ежемесячно
вносить в банк $15, $20 или $25, то Вы станете миллионером через 45, 43 или 41 год, соответственно.
3.5.ЗАДАНИЯ ДЛЯ САМОСТОЯТЕЛЬНОЙ РАБОТЫ
Функция БЗ() [ПС] Задание 3-1
Рассчитать какая сумма окажется на счете, если 27 тыс. руб. положены на 33 года под 13.5% годовых. Проценты начисляются каждые полгода
Ответ: 2 012 074.64р
Задание 3-2
3. У Вас есть возможность ежегодно в течение 4 лет инвестировать 300 тыс. руб. в два проекта:под 26% в начале каждого года или 38% в конце года.
Определите, какой из вариантов вложения средств предпочтительнее.
Ответ:
а) 2 210,53р. б) 2 073,74р.
76
Задание 3-3
.На сберегательный счет вносятся платежи по 200 тыс. руб. в начале месяца а)Рассчитайте, какая сумма окажется на счете через 4 года при ставке процента 5%,
7.5%, 10%, 12.5%, 15.5%, 20%.
б) Повторите этот расчет для случая, если платежи вносятся в конце месяца в) Постройте диаграмму, иллюстрирующую выполненные расчеты Примечание Для решения задачи используйте «Таблицу подстановок Ответ
|
Началомесяца |
|
конецмесяца |
|
|
|
|
Процент |
9600,00 |
Процент |
9600,00 |
0,05 |
10647,16 |
0,05 |
10602,98 |
0,08 |
11224,89 |
0,08 |
11155,17 |
0,10 |
11842,37 |
0,10 |
11744,50 |
0,13 |
12502,58 |
0,13 |
12373,69 |
0,15 |
13208,75 |
0,15 |
13045,68 |
|
|
|
|
0,20 |
14773,16 |
0,20 |
14530,98 |
Накопление сумм при различных ставках
сумма |
15000 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
14000 |
|
|
в начале |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
Накопленная |
13000 |
|
|
месяца |
|
|
|
|
|
|
12000 |
|
|
|
|
В конце |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
11000 |
|
|
|
|
месяца |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
10000 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
5,00% |
10,00% |
15,00% |
20,00% |
25,00% |
|||||
|
|
|
|
|
ставка процента |
|
|
|||
Задание 3-4
Вы хотите зарезервировать деньги для специального проекта, который будет осуществлен через год. Предположим, Вы собираетесь вложить 1000 рублей под 6% годовых (что составит в месяц 6%/12 или 0,5%). Вы собираетесь вкладывать по 100 рублей в начале каждого следующего месяца в течение следующих 12 месяцев.
Сколько денег будет на счету в конце 12 месяцев? Ответ: 2301,40 р
Задание 3-5
Фирма создает фонд для погашения долгосрочных обязательств, срок которых истекает через пять лет, путем ежегодного пополнения депозита, с начальной суммой 10000 тыс. руб. Размер ежегодного взноса 1000 тыс. руб. Ставка по депозиту – 5% годовых, начисляемых в конце каждого периода. Определите величину фонда к концу пятого года.
Ответ: 18288,45 тыс. руб
Функция ПЗ() [ПС[ Задание 3-6
Вы решили приобрести автомобиль стоимостью 200000 руб. Какую сумму Вы должны вложить в банк под 12% годовых для того, чтобы иметь возможность его приобретения.
а) Начисление процентов производится один раз в начале года б) Начисления производятся 2 раза в год в начале периода.
Ответ: а) |
-178 |
571.43р. |
б) |
-177 |
697.41р |
Задание 3-7
Предположим, что выкупается страховка, по которой выплачивается по 500 руб. в конце каждого месяца в течение 20 последующих лет. Стоимость ренты составляет 60 000 руб. и выплачиваемые деньги принесут 8 процентов годовых. Необходимо определить, будет ли это хорошим способом инвестировать капитал.
77
Ответ: -59 777,15 руб, Настоящий объем вклада (59 777,15 руб.) меньше, чем запрашиваемая цена (60 000 руб.). Следовательно, можно сделать вывод, что это не самый лучший способ инвестирования денег.
Функция КПЕР() Задание 3-8
4.Для обеспечения будущих расходов создается фонд. Средства в фонд поступают в виде постоянной годовой ренты. Размер разового платежа составляет 16 млн. руб. На поступившие взносы начисляется 11.18% годовых.
Определить, когда величина фонда будет равна 100 мл. руб.
Ответ: 4,99 года
Задание 3-9
По вкладу в 10000,00, помещенному в банк под 5% годовых, начисляемых ежегодно, была выплачена сумма 12762,82.
а) Определить срок проведения операции (количество периодов начисления). б) используя построение сценария, выясните как влияет банковский процент ( в
диапазоне от 1% до 10 %) на срок получения |
|
|
влияние величины банковского |
||
указанной суммы банковский процент. Постройте |
||
процентанасрок получения |
||
диаграмму, отражающую эту зависимость. |
||
заданной суммы |
||
Ответ: а) 5 лет |
|
|
ле |
30.00 |
|
|
|
|
|
|
|
(кол. |
|
|
|
|
|
|
|
Задание 3-10 |
20.00 |
|
|
|
-0.9811 |
|
|
|
|
|
|
|
|
|
|||
|
|
|
y = 0.2656x |
|
|
|||
срок |
10.00 |
|
|
|
|
|||
0.00 |
|
|
|
|
|
|
||
Ожидается, что ежегодные доходы от |
|
|
|
|
|
|
||
|
|
|
|
|
|
|
||
|
0.00% |
2.00% |
4.00% |
6.00% |
8.00% |
10.00% |
12.00% |
|
|
|
|
|
|
|
|
|
|
реализации проекта составят 33млн. руб. |
|
|
|
банковскийпроцент |
|
|
||
|
|
|
|
|
|
|
|
|
а) Рассчитайте срок окупаемости проекта, |
|
|
|
|
|
|
|
|
если инвестиции к началу поступления доходов составят 100мл.руб., а норма |
|
|
|
|||||
дисконтирования – 12.11%. |
|
|
|
|
|
|
|
|
б) Используя таблицу подстановки, рассчитайте: |
|
|
|
|
|
|
|
|
Как будет изменяться срок окупаемости проекта в зависимости от нормы |
|
|
|
|||||
дисконтирования (от 1% до 20%). Постройте диаграмму, иллюстрирующую эту |
|
|
|
|||||
зависимость; |
|
|
|
|
|
|
|
|
Как будет изменяться срок окупаемости проекта в зависимости от нормы |
|
|
|
|||||
дисконтирования (от 1% до 20%) и величины инвестиции к началу поступления доходов |
|
|||||||
(50 до 150млн. руб.). Постройте диаграмму, иллюстрирующую эту зависимость. |
|
|
|
|||||
Ответ: а) 4 года |
|
|
|
|
|
|
|
|
|
срок окупаемости проекта в зависмости от |
срок окупаемости проекта в зависимости от ставки дисконтирования и |
||||||||||||||||
|
|
ставки дисконтирования |
|
|
|
|
|
|
|
величины инвестиции |
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
10-12 |
|
5 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
8-10 |
окупаемости |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
4.5 |
|
|
|
|
|
12 |
|
|
|
|
|
|
|
|
|
|
6-8 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
4 |
|
|
|
|
|
10 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
4-6 |
||
|
|
|
|
|
|
8 |
|
|
|
|
|
|
|
|
|
|||
срок |
3.5 |
|
|
|
|
срок окупаемости |
6 |
|
|
|
|
|
|
|
|
|
2-4 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
4 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
3 |
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0-2 |
|
|
0.00% |
5.00% |
10.00% |
15.00% |
20.00% |
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
процент дисконта |
|
|
|
|
|
|
|
|
|
|
|
|
|
-125 |
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
% |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
.0 |
|
|
|
|
|
|
|
|
|
инвестиции |
|
|
|
|
|
|
|
|
1 |
|
|
|
|
% |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
.0 |
|
|
|
|
|
|
-50 |
|
|
|
|
|
|
|
|
|
|
|
7 |
|
|
|
|
% |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
.0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
3 |
|
|
|
% |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
.0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
9 |
|
|
|
|
|
|
|
|
|
|
|
|
проценты |
|
|
|
1 |
|
|
||

78
Функции БЗРАСПИС();ЭФФЕКТ(); СТАВКА(); Задание 3-11
1. Ставка банка по срочным валютным депозитам на начало года составляет 20% годовых,
начисляемых раз в квартал. Первоначальная сумма вклада - $1000. В течении года ожидается снижение ставок раз в квартал на 2, 3 и 5 процентов соответственно.
Определить величину депозита к концу года.
Ответ: 1186.78
Задание 3-12
Ставка банка по срочным валютным депозитам составляет 18% годовых. Какова реальная доходность вклада (т.е. эффективная ставка) если проценты выплачиваются:
а) ежемесячно б) раз в год Ответ: a) 0.20
б) 0.18
Задание 3-13
Компании Х потребуется 100000 тыс. руб. через 2 года.
а) Компания готова вложить 5000 тыс. руб. сразу и по 2500 тыс. руб. каждый
последующий месяц. Каким должен быть процент на инвестированные средства, чтобы получить необходимую сумму в конце второго года.
б) Компания отказалась от ежемесячных платежей и готова единовременно вложить 40000 тыс. руб.. Определите, как изменится в этом случае процентная ставка.
Месячн. Ставка |
Годовая ставка |
|
Ответ: а) |
3.28% |
39.36% |
б) |
3.89% |
46.70% |
Задание 3-14
Рассчитайте процентную ставку для четырехлетнего займа в 7000 тыс. руб. с ежемесячным погашением по 250 тыс. руб. при условии, что заем полностью погашается
Ответ: 2,46% в месяц или 29,5% годовых
79
4. ОЦЕНКА ИНВЕСТИЦИОННЫХ ПРОЦЕССОВ
Инвестиции – это долгосрочные финансовые вложения экономических ресурсов с целью создания и получения выгоды в будущем, которая должна быть выше начальной величины вложений.
Инвестиционный процесс – это последовательность связанных инвестиций, растянутых во времени, отдача от которых также распределена во времени. Этот процесс характеризуется двусторонним потоком платежей, где отрицательные члены потока являются вложениями денежных средств в инвестиционный проект, а положительные члены потока – доходы от инвестированных средств.
Методы измерения доходности инвестиционных проектов основаны на анализе равномерного денежного потока. Ожидаемые значения элементов денежного потока, соответствующие будущим периодам, являются результатом сальдирования всех статей доходов и расходов, связанных с осуществлением проекта.
Для приведения значений элементов денежного потока к сопоставимому во времени виду по выбранной норме дисконтирования оценивается суммарная текущая стоимость на момент принятия решения о вложении капитала, предшествующий началу движения средств. Уровень процентной ставки, применяемой в качестве нормы дисконтирования, должен соответствовать длине периода, разделяющего элементы денежного потока.
В качестве показателей эффективности инвестиционных проектов обычно используются:
чистый приведенный доход – текущая стоимость всех доходов и расходов по проекту;
срок окупаемости – характеризует срок окупаемости средств, вложенных (инвестированных) в проект;
внутренняя норма доходности – это ставка дисконтирования, приравнивающая сумму приведенных доходов от инвестиционного проекта к величине инвестиций, т.е. вложения окупаются, но не приносят прибыль.
4.1.ЧИСТЫЙ ПРИВЕДЕННЫЙ ДОХОД
При оценке инвестиционных проектов используется метод расчета чистого приведенного дохода, который предусматривает дисконтирование денежных потоков: все доходы и затраты приводятся к одному моменту времени.
Центральным показателем в рассматриваемом методе является показатель NPV (net present value) – текущая стоимость денежных потоков за вычетом текущей стоимости денежных оттоков. Это обобщенный конечный результат инвестиционной деятельности в абсолютном измерении.
При разовой инвестиции расчет чистого приведенного дохода можно представить следующим выражением:
n |
CFk / (1 |
+ r)k |
|
NPV = ∑ |
− Z0 |
||
k=1 |
|
|
( 4-1) |
|
|
где CFk – годовые денежные поступления в течение n лет, k = 1, 2, …, n; Z – стартовые инвестиции;
80
r – ставка дисконтирования.
Если проект предполагает не разовую инвестицию, а последовательное инвестирование финансовых ресурсов в течение нескольких лет (m), то формула для расчета модифицируется:
n |
|
+ r)k |
m |
|
|
|
NPV = ∑ |
CFk / (1 |
− ∑ Zj / (1 |
+ r)j |
|
||
k=1 |
|
|
j=1 |
|
|
( 4-2) |
|
|
|
|
|||
Показатель NPV характеризует абсолютный прирост40, поскольку оценивает, на сколько приведенный доход перекрывает приведенные затраты:
при NPV > 0 проект может быть принят;
при NPV < 0 проект не принимается,
при NPV = 0 проект не имеет ни прибыли, ни убытков
Пример 4-1
Найти чистый дисконтированный доход проекта, требующего стартовых инвестиций в объеме 150 тыс. руб., денежный поток которого задан рис.6-1, по ставке дисконтирования 10% годовых.
Рис. 4-1 Денежный поток инвестиционного проекта
Решение
170.00 |
CF |
|
|
|
|
125 |
|
|
|
|
|
|
|
|
|
||
|
|
|
|
100 |
|
100 |
100 |
|
120.00 |
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
70.00 |
|
|
|
55 |
|
|
|
|
|
|
25 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
20.00 |
|
|
|
|
|
|
|
|
-30.00 |
|
|
|
|
|
|
|
|
-80.00 |
|
|
-50 |
|
|
|
|
|
-70 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
-130.00 |
-150 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
-180.00 |
|
|
|
|
|
|
|
|
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
|
|
|
Время(год) |
|
|
|
||
На листе Excel создадим таблицу, подобную приведенной на Рис.4-2.
40 Необходимо отметить, что показатель NPV отражает прогнозную оценку изменения экономического потенциала фирмы в случае принятия данного проекта.
