
Finansovaya_matematika_v_Excel_Levin_L_A
.pdf
Министерство науки и образования Российский государственный социальный университет
Красноярский филиал
Левин Л.А.
(Учебно – методичекое пособие для студентов экономических специальностей всех форм обучения)
Красноярск. 2006.
2
Левин Л.А. "Финансовая математика": Учебное - методическое пособие.
Рецензенты:
зав. кафедрой Информатики «Финансы и кредит» КФ РГСУ доцент И.З. Погорелов декан ФИФТ КГПУ, к.т.н., проф. Е.А Вейсов
Учебное пособие предназначено для освоения дисциплины "Финансовая математика”, а также для тех дисциплин, где изучаются разделы, связанные с вопросами оценки финансовых операций.
Предназначено для студентов экономических специальностей всех форм обучения.
Пособие рассчитано на широкое использование электронной таблицы Excel и содержит основные теоретические положения, рассматриваемых в ней вопросов, примеры решения задач, вопросы по отдельным разделам. задания для самостоятельного выполнения и библиографию.
.
Рассмотрено на заседании кафедры
Протокол № ___
“___”_ ______2006__г.
СОДЕРЖАНИЕ |
|
ВВЕДЕНИЕ ............................................................................................................................................. |
5 |
ФИНАНСОВАЯ МАТЕМАТИКА – ЧТО ЭТО? ............................................................................................. |
5 |
ФАКТОР ВРЕМЕНИ В ФИНАНСОВО-ЭКОНОМИЧЕСКИХ РАСЧЕТАХ.......................................................... |
6 |
MS EXCEL – ОСНОВНОЙ ИНСТУМЕНТ ДЛЯ ВЫПОЛНЕНИЯ ФИНАНСОВО-ЭКОНОМИЧЕСКИХ РАСЧЕТОВ7 |
|
КАК РАБОТАТЬ С УЧЕБНЫМ ПОСОБИЕМ?............................................................................................... |
8 |
1.ИЗМЕНЕНИЕ СТОИМОСТИ ВЛОЖЕНИЙ ЗА СЧЕТ
ПРИСОЕДИНЕНИЯ ПРОЦЕНТОВ............................................................................................................... |
10 |
|
1.1. |
ОСНОВНЫЕ КАТЕГОРИИ ФИНАНСОВО-ЭКОНОМИЧЕСКИХ РАСЧЕТОВ.................................... |
11 |
1.1.1. Тесты для проверки усвоения пройденного материала .............................................. |
14 |
|
1.2. |
ПРОСТЫЕ ПРОЦЕНТЫ............................................................................................................ |
15 |
1.2.1. Временная база финансовой операции ......................................................................... |
16 |
|
1.2.2. |
Переменная ставка........................................................................................................ |
18 |
1.2.3. Определение срока ссуды и величины процентной ставки......................................... |
19 |
|
1.2.4. Тесты для проверки усвоения пройденного материала .............................................. |
20 |
|
1.2.5. Задачи для самостоятельного решения....................................................................... |
21 |
|
1.3. |
СЛОЖНЫЕ ПРОЦЕНТЫ........................................................................................................... |
23 |
1.3.1. Начисление процентов при дробных периодах ............................................................ |
27 |
|
1.3.2. |
Эффективная ставка процентов................................................................................. |
28 |
1.3.3. |
Непрерывное начисление процентов ............................................................................ |
30 |
1.3.4. |
Переменная ставка процентов..................................................................................... |
31 |
1.3.5. Определение срока ссуды и величины процентной ставки......................................... |
32 |
|
1.3.6. Тесты для проверки качества усвоения пройденного материала.............................. |
32 |
|
1.3.7. Задачи для самостоятельного решения....................................................................... |
34 |
|
1.4. |
ДИСКОНТИРОВАНИЕ ............................................................................................................. |
36 |
1.4.1. |
Математическое дисконтирование............................................................................. |
36 |
1.4.2. |
Банковский учет............................................................................................................. |
38 |
1.4.3. |
Тест для проверки качества усвоения пройденного материала ............................... |
40 |
1.4.4. Задачи для самостоятельного решения....................................................................... |
41 |
|
2. ИСПОЛЬЗОВАНИЕ ВСТРОЕННЫХ ФУНКЦИЙ MS EXCEL......................................... |
43 |
|
2.1. |
ТЕХНОЛОГИЯ РАБОТЫ С ФИНАНСОВЫМИ ФУНКЦИЯМИ EXCEL ............................................ |
43 |
2.1.1. Операции наращения. Функция БС() ............................................................................ |
49 |
|
2.1.2. |
Операции дисконтирования.......................................................................................... |
51 |
2.1.3. Определение срока финансовой операции.................................................................... |
52 |
|
2.1.4. |
Определение процентной ставки ................................................................................. |
53 |
2.1.5. Расчет эффективной и номинальной ставки процентов........................................... |
54 |
|
2.1.6. Начисление процентов по плавающей ставке............................................................. |
55 |
|
3. ПОТОКИ ПЛАТЕЖЕЙ И ФИНАНСОВЫЕ РЕНТЫ.......................................................... |
57 |
|
3.1. |
ДЕНЕЖНЫЕ ПОТОКИ В ВИДЕ СЕРИИ РАВНЫХ ПЛАТЕЖЕЙ (АННУИТЕТЫ)............................... |
58 |
3.2. |
КЛАССИФИКАЦИЯ ФИНАНСОВЫХ РЕНТ ................................................................................ |
58 |
3.3. |
РАСЧЕТ ПЕРИОДИЧЕСКИХ ПЛАТЕЖЕЙ................................................................................... |
60 |
3.3.1.Определение будущей (наращенной) стоимости потока платежей. Функция БС()60
3.3.2. Современная (текущая) величина аннуитета. Функция ПС() ................................... |
62 |
|
3.3.3. Нерегулярные потоки платежей, Функция БЗРАСПИС().......................................... |
64 |
|
3.3.4. |
Определение величины периодического платежа. Функция ПЛТ()........................... |
66 |
3.3.5. Расчет платежей по процентам. Функция ПРПЛТ() ................................................ |
67 |
|
3.3.6. Расчет суммы платежей по процентам по займу. Функция ОБЩПЛАТ().............. |
69 |
|
3.3.7. Расчет величины основных платежей по займу. Функция ОСПЛТ()........................ |
70 |
|
3.3.8. Расчет суммы основных платежей по займу. Функция ОБЩДОХОД()................... |
71 |
|
3.3.9. Использование операции «Подбор параметра» для определения |
|
|
отдельных параметров аннуитета......................................................................................................... |
71 |
|
3.4. |
РАЗРАБОТКА ШАБЛОНА ДЛЯ АНАЛИЗА АННУИТЕТОВ ........................................................... |
73 |
3.5. |
ЗАДАНИЯ ДЛЯ САМОСТОЯТЕЛЬНОЙ РАБОТЫ......................................................................... |
75 |
4. ОЦЕНКА ИНВЕСТИЦИОННЫХ ПРОЦЕССОВ ................................................................ |
79 |
|
4.1. |
ЧИСТЫЙ ПРИВЕДЕННЫЙ ДОХОД ........................................................................................... |
79 |
4.2. |
СРОК ОКУПАЕМОСТИ............................................................................................................ |
83 |
4.3. |
ИНДЕКС РЕНТАБЕЛЬНОСТИ ................................................................................................... |
85 |
4
4.3.1. |
Внутренняя норма доходности. Функция ЧИСТВНДОХ()......................................... |
87 |
4.3.2. |
Модифицированная внутренняя норма доходности. Функция МСВД().................... |
88 |
4.4.ДЕНЕЖНЫЙ ПОТОК ИНВЕСТИЦИОННОГО ПРОЕКТА С ПРОИЗВОЛЬНЫМИ ПЕРИОДАМИ
ПОСТУПЛЕНИЯ ПЛАТЕЖЕЙ ................................................................................................................................ |
89 |
||
|
4.5. |
ЗАДАЧИ ДЛЯ САМОСТОЯТЕЛЬНОГО РЕШЕНИЯ ...................................................................... |
91 |
5. |
ЛИТЕРАТУРА............................................................................................................................ |
99 |
|
6. |
ПРИЛОЖЕНИЯ ....................................................................................................................... |
100 |
|
|
6.1. |
ПРИЛОЖЕНИЕ 1. ОСНОВНЫЕ ТЕХНОЛОГИЧЕСКИЕ ПРИЕМЫ РАБОТЫ В MS EXCEL ............. |
100 |
|
6.1.1. Перемещение по рабочему листу................................................................................ |
101 |
|
|
6.1.2. Основные правила ввода данных в ячейку таблицы.................................................. |
102 |
|
|
6.1.3. |
Подбор параметра ...................................................................................................... |
103 |
|
6.1.4. |
Диспетчер сценариев................................................................................................... |
105 |
|
6.1.5. |
Таблица подстановки .................................................................................................. |
107 |
|
6.2. |
ПРИЛОЖЕНИЕ 2. ПОРЯДКОВЫЕ НОМЕРА ДНЕЙ В НЕ ВИСОКОСНОМ ГОДУ........................... |
109 |
|
6.3. |
ПРИЛОЖЕНИЕ 3. МНОЖИТЕЛИ НАРАЩЕНИЯ ПО СЛОЖНЫМ ПРОЦЕНТАМ ........................ |
110 |
5
ВВЕДЕНИЕ
В настоящее время трудно переоценить роль специалиста по финансовому анализу деятельности предприятия. Финансы являются “кровью” предприятия. Именно в деньгах оцениваются проданные товары и оказанные клиентам услуги. Именно деньги являются универсальным измерителем необходимых предприятию ресурсов − сырья и материалов, станков, человеческих ресурсов, информации и т.д. Поэтому планирование и прогнозирование, контроль и оптимизация финансовых потоков являются жизненно важными задачами финансовой службы.
Решению этих задач посвящен курс «Финансовая математика».
ФИНАНСОВАЯ МАТЕМАТИКА – ЧТО ЭТО?
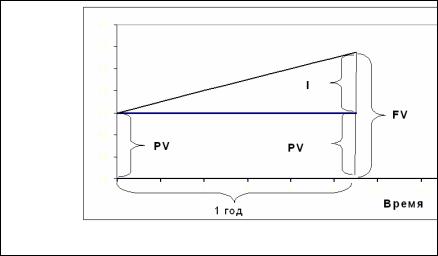
Под финансовой математикой понимаются модели и алгоритмы финансовых расчетов. Базовая финансовая операция – кредитование. Субъекты рынка заключают сделку: кредитор выдает заемщику ссуду с условием, что в установленный срок заемщик вернет кредитору ссуду с наращением (процентами). Ситуация в простейшем случае, когда ссуда выдана на год, показана на рис.1-1.
Деньги
Финансовая операция. (PV – сумма (ссуда), выданная кредитором заемщику; FV – сумма, получаемая кредитором по окончании финансовой операции; I – доход, получаемый кредитором.)
Лучшее, на наш взгляд, определение сущности финансовой математики дано Е.М. Четыркиным, который отмечал, что финансовая математика представляет собой совокупность методов определения изменения стоимости денег, происходящего вследствие их возвратного движения в процессе воспроизводства. Таким образом, финансовая математика – раздел количественного анализа финансовых операций, предметом которого является изучение функциональных зависимостей между параметрами коммерческих сделок или финансово-
6
банковских операций и разработка на их основе методов решения финансовых задач определенного класса.
Объектом изучения финансовой математики является финансовая операция, в которой необходимость использования финансово-экономических вычислений возникает всякий раз, когда в условиях сделки (финансовой операции) прямо или косвенно присутствуют временные параметры: даты, сроки выплат, периодичность поступления денежных средств, отсрочка платежей и т.д. При этом фактор времени зачастую играет более важную роль, чем стоимостные характеристики финансовой операции, поскольку именно он определяет конечный финансовый результат
ФАКТОР ВРЕМЕНИ В ФИНАНСОВО-ЭКОНОМИЧЕСКИХ РАСЧЕТАХ
Известный всем лозунг "время – деньги" имеет под собой реальную основу, позволяющую определить истинную ценность денег с позиции текущего момента. Время не возвращается, но вложенный в дело капитал, может со временем прирасти и вернуться к инвестору с процентом. Кредитор взимает плату за использование денежных средств с заемщика, который намерен потратить их именно сейчас, так как предпочитает удовлетворять свои потребности раньше, чем накопит достаточно собственных средств.
Важность учета фактора времени обусловлена принципом неравноценности денег, относящихся к различным моментам времени:
Равные по абсолютной величине денежные суммы "сегодня" и "завтра" оцениваются по разному, – сегодняшние деньги ценнее будущих.
Отмеченная зависимость ценности денег от времени обусловлена влиянием фактора времени:
во-первых, деньги можно продуктивно использовать во времени как приносящий доход финансовый актив, т.е. деньги могут быть инвестированы и тем самым принести доход. Рубль в руке сегодня стоит больше, чем рубль, который должен быть получен завтра ввиду процентного дохода, который вы можете получить, положив его на сберегательный счет или проведя другую инвестиционную операцию;во-вторых, инфляционные процессы ведут к обесцениванию денег во времени.
Сегодня на рубль можно купить товара больше, чем завтра на этот же рубль, т.к. цены на товар повысятся;в-третьих, неопределенность будущего и связанный с этим риск повышает
ценность имеющихся денег. Сегодня рубль в руке уже есть и его можно израсходовать на потребление, а будет ли он завтра в руке, – еще вопрос. Для корректности арифметического сопоставления величин разновременных затрат/доходов их необходимо корректировать, т.е., используя некоторые финансовые коэффициенты, основанные на формулах начисления процентов,
привести к одному и тому же моменту времени. Эти коэффициенты учитывают возможный уровень отдачи инвестиций при выбранном уровне риска за период, разделяющий показатели во времени.
Приведение более ранней суммы к эквивалентной ей величине в другой момент времени в будущем производится ее умножением на коэффициент наращения.

7
Рост по правилу простых процентов является линейным и подчиняется закону арифметической прогрессии, а правило сложных процентов порождает геометрическую прогрессию.
Эффективная доходность вложений зависит от правила и частоты начисления процентов.
Реальная доходность ниже уровня процентной ставки в связи с дополнительным взиманием налогов и комиссионных за операцию, а также в связи с инфляцией. Начисление процентов, как правило, производится дискретно, т.е. за фиксированные одинаковые интервалы времени, которые носят название "период начисления", – это отрезок времени между двумя следующими друг за другом процедурами взимания процентов. Обычные или декурсивные (postnumerando) проценты начисляются в конце периода. Как правило, в качестве единицы периода времени в финансовых расчетах принят год, однако это не исключает использования периода менее года: полугодие, квартал, месяц, день, час.
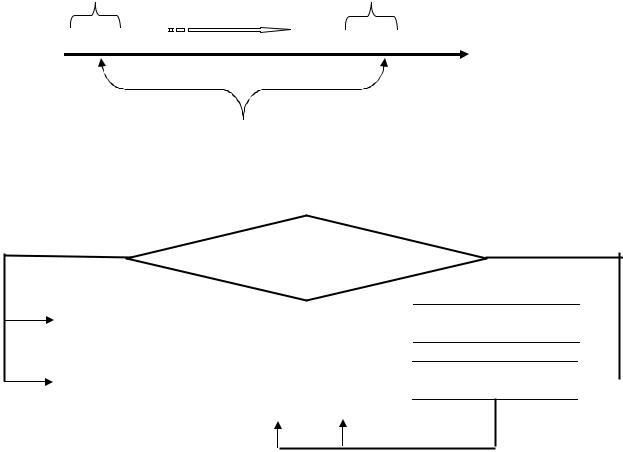
Период времени от начала финансовой операции до ее окончании называется сроком финансовой операции
|
|
Первое |
|
Второе |
|
N -e |
|
||||||
Начало |
|
начисления |
|
начисление |
|
начисление |
операции |
|
процентов |
|
процентов |
|
процентов |
|
|
|
|
|
|
|
период |
t – (время) |
Период начисления процентов
MS EXCEL – ОСНОВНОЙ ИНСТУМЕНТ ДЛЯ ВЫПОЛНЕНИЯ ФИНАНСОВО-ЭКОНОМИЧЕСКИХ РАСЧЕТОВ
Сегодня нельзя всерьез претендовать на работу экономиста, менеджера, бухгалтера, финансиста, специалиста по ценным бумагам и т.п., если не уметь обращаться с компьютером. Умение работы с компьютером предполагает прежде всего знание текстовых процессоров, электронных таблиц, системы управления базами данных и систем для работы с графикой.
EXCEL является одной из самых популярных программ работающих в операционной среде Windows, сочетающей возможности графического и текстового редакторов с мощной математической поддержкой, позволяющей решать задачи практически любой степени сложности. К числу несомненных достоинств MS Excel следует отнести и то, что даже неопытный пользователь, владеющий только основными приемами работы, без особых затруднений может создать свои собственные программы–шаблоны, позволяющие автоматизировать выполнение необходимых расчетов и полностью отказаться от использования калькулятора.
Не вызывает сомнения то, что Вы хорошо достаточно хорошо знакомы с техникой работы в MS Excel и при решении приводимых в тексте примеров и задач, Вы будете выполнять их именно в среде MS Excel. В случае затруднений Вы можете воспользоваться описанием основных технологических приемов

8
работы в MS Excel, приведенных в Приложении 1, либо любым руководством по этому программному продукту.
КАК РАБОТАТЬ С УЧЕБНЫМ ПОСОБИЕМ?
Учебно-методическое пособие содержит изложение основных понятий и методов финансовых вычислений и количественного анализа финансовых операций, охватывает базовые разделы финансовой математики, и направлено на построение планов погашения кредитов и финансового анализа инвестиций1.
В основе излагаемого материала лежит учет роли фактора времени в финансовых операциях и возникающим в процессе их проведения потоков платежей. При этом особое внимание уделяется основным количественным показателям, характеризующим финансовые сделки, на конкретных примерах показаны методы их исчисления, а также технология автоматизации базовых расчетов в среде ППП
EXCEL.
Базовые разделы финансовой математики и опирающиеся на них прикладные финансовые расчеты сопровождаются использованием технологий встроенных функций табличного процессора Excel.
Помимо удобного средства автоматизации многочисленных и трудоемких расчетов, он сыграет здесь роль своеобразного компьютерного полигона, где в процессе решения конкретных задач Вы сможете убедиться на практике в справедливости и полезности рассмотренных теоретических концепций. Следует отметить, что несмотря на то, что реализация большинства моделей и
методов вычислений в среде ППП EXCEL рассматривается достаточно подробно (практически на уровне пошаговых инструкций) и не требует специальной подготовки в области информатики и программирования ЭВМ, мы все же предполагаем наличие у читателя элементарного практического опыта работы c Windows и ППП EXCEL , а также знания клавиатуры ПЭВМ и умения обращаться с устройством "мышь". Рекомендации по установке ППП EXCEL и настройке панелей инструментов приведены в приложении 1.
Все рассмотренные в книге примеры и разработанные в виде специальных шаблонов модели для решения типовых задач прошли тестирование в локализованных версиях ППП EXCEL и при необходимости могут быть использованы в повседневной практической деятельности читателя.
Каждая глава снабжена материалами для практической работы на персональном компьютере, вопросами для повторения и контроля степени усвоения
1 Данное пособие, безусловно, не может полностью охватить предмета «Финансовая математика» и задумано как настольная книга пользователя ПК, помогающая ему, во-первых, самостоятельно изучить основные формулы процентных расчетов и, во-вторых, научиться работать с ними в электронных таблицах.
Принятые в настоящем учебном пособии состав и последовательность рассмотрения учебного материала, позволяют получить целостное представление о финансово-экономических расчетах и о практическом применении этих методов при разработке и реализации финансовых решений.
9
пройденного материала. Это позволяет использовать ее как для самостоятельного обучения, так и в качестве учебного пособия по соответствующим разделам курсов: “Финансовый менеджмент”, "Ценные бумаги", “Информационные технологии финансово-кредитной и банковской деятельности и др..
Мы надеемся, что предлагаемая работа окажется полезной для студентов и аспирантов экономических вузов, а также всем, кто интересуется данной тематикой.
1.ИЗМЕНЕНИЕ СТОИМОСТИ ВЛОЖЕНИЙ ЗА СЧЕТ ПРИСОЕДИНЕНИЯ ПРОЦЕНТОВ
Рассмотрим процесс наращения (accumulation), т.е. определения денежной суммы в будущем, исходя из заданной суммы сейчас.
Экономический смысл операции наращения состоит в определении величины той суммы, которой будет или желает располагать инвестор по окончании этой операции. Здесь идет движение денежного потока от настоящего к будущему.
Величина FV показывает будущую стоимость "сегодняшней" величины инвестиции PV при заданном уровне интенсивности начисления процентов r
PV |
FV |
t– время
Рис. 1-1 Логическая схема операции наращения
Существуют различные способы начисления процентов и соответствующие им виды процентных ставок
Процентная ставка
Простая |
|
|
|
|
|
|
Постоянная |
|
Переменная |
||
|
|
|
|||
|
|||||
Сложная |
|||||
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|

 Плавающая
Плавающая












 Фиксированная
Фиксированная




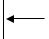

Рис. 1-2 Типы процентных ставок
|
применяется к одной и той же первоначальной |
Простая процентная ставка |
сумме долга на протяжении всего срока ссуды, т.е. |
|
исходная база (денежная сумма) всегда одна и та |
|
же. |
|
применяется к наращенной сумме долга, т.е. к |
Сложная процентная ставка |
сумме, увеличенной на величину начисленных за |
|
предыдущий период процентов, – таким образом, |
|
исходная база постоянно увеличивается. |
