
- •ВВЕДЕНИЕ В
- •Литература
- •Решебники
- •Логические символы
- •МНОЖЕСТВА
- •Числовые множества
- •Включение множеств
- •ЧИСЛОВЫЕ МНОЖЕСТВА
- •ОСНОВНЫЕ ОПЕРАЦИИ НАД МНОЖЕСТВАМИ
- •Объединение множеств
- •Пересечение множеств
- •Вычитание множеств
- •ПОНЯТИЕ
- •ОБЛАСТЬ ОПРЕДЕЛЕНИЯ ФУНКЦИИ
- •КЛАССИФИКАЦИЯ ВЕЩЕСТВЕННЫХ ФУНКЦИЙ, ВЕЩЕСТВЕННОГО АРГУМЕНТА
- •элементарные
- •ОСНОВНЫЕ ХАРАКТЕРИСТИКИ ПОВЕДЕНИЯ ФУНКЦИИ
- •ЧИСЛОВАЯ ПОСЛЕДОВАТЕЛЬНОСТЬ И ЕЕ ПРЕДЕЛ
- •ОПРЕДЕЛЕНИЕ ЧИСЛОВОЙ
- •ОГРАНИЧЕННЫЕ И НЕОГРАНИЧЕННЫЕ ПОСЛЕДОВАТЕЛЬНОСТИ
- •ОГРАНИЧЕННЫЕ
- •ОГРАНИЧЕННЫЕ И
- •ПРИМЕРЫ
- •МОНОТОННЫЕ
- •ПРИМЕР
- •ЛЕКЦИЯ №2 ПО МАТЕМАТИЧЕСКОМУ АНАЛИЗУ
- •ОПРЕДЕЛЕНИЕ ПРЕДЕЛА
- •ЗАМЕЧАНИЕ
- •ПРИМЕР
- •ПРИМЕР
- •ГЕОМЕТРИЧЕСКАЯ ИНТЕРПРЕТАЦИЯ ПРЕДЕЛА ЧИСЛОВОЙ ПОСЛЕДОВАТЕЛЬНОСТИ
- •ПРИЗНАК СХОДИМОСТИ МОНОТОННОЙ ПОСЛЕДОВАТЕЛЬНОСТИ
- •БЕСКОНЕЧНО МАЛЫЕ И БЕСКОНЕЧНО БОЛЬШИЕ ВЕЛИЧИНЫ
- •БЕСКОНЕЧНО МАЛЫЕ ВЕЛИЧИНЫ
- •ПРИМЕР
- •БЕСКОНЕЧНО БОЛЬШАЯ ВЕЛИЧИНА
- •ПРИМЕР
- •ПОЛОЖИТЕЛЬНАЯ БЕСКОНЕЧНО БОЛЬШАЯ ВЕЛИЧИНА
- •ОТРИЦАТЕЛЬНАЯ БЕСКОНЕЧНО БОЛЬШАЯ ВЕЛИЧИНА
- •ГЕОМЕТРИЧЕСКАЯ ИНТЕРПРЕТАЦИЯ БЕСКОНЕЧНО БОЛЬШОЙ ВЕЛИЧИНЫ
- •ЗАМЕЧАНИЕ
- •БЕСКОНЕЧНО БОЛЬШОЙ И БЕСКОНЕЧНО МАЛОЙ ВЕЛИЧИНАМИ !!!
- •АРИФМЕТИЧЕСКИЕ ДЕЙСТВИЯ НАД ПЕРЕМЕННЫМИ ВЕЛИЧИНАМИ. ОСНОВНЫЕ ТЕОРЕМЫ О ПРЕДЕЛАХ ПЕРЕМЕННЫХ
- •ТЕОРЕМЫ О ПРЕДЕЛАХ ПЕРЕМЕННЫХ
- •ТЕОРЕМЫ О ПРЕДЕЛАХ ПЕРЕМЕННЫХ
- •ТЕОРЕМЫ О ПРЕДЕЛАХ ПЕРЕМЕННЫХ
- •ОСНОВНЫЕ ТЕОРЕМЫ О ПРЕДЕЛАХ ПЕРЕМЕННЫХ
- •ОСНОВНЫЕ ТЕОРЕМЫ О ПРЕДЕЛАХ ПЕРЕМЕННЫХ
- •ОСНОВНЫЕ ТЕОРЕМЫ О ПРЕДЕЛАХ ПЕРЕМЕННЫХ
- •ПРИМЕР
- •СВОЙСТВА БЕСКОНЕЧНО БОЛЬШИХ ВЕЛИЧИН
- •ПРИМЕРЫ
- •ЗАМЕЧАНИЕ
- •НЕОПРЕДЕЛЕННОСТЬ
- •ПРИМЕР РАСКРЫТИЯ НЕОПРЕДЕЛЕННОСТИ ВИДА
- •НЕОПРЕДЕЛЕННОСТЬ
- •НЕОПРЕДЕЛЕННОСТЬ
- •ЛЕКЦИЯ
- •ПРЕДЕЛ
- •ОПРЕДЕЛЕНИЕ
- •ОПРЕДЕЛЕНИЕ ПРЕДЕЛА ФУНКЦИИ ПО КОШИ ( НА ЯЗЫКЕ )
- •ОПРЕДЕЛЕНИЕ
- •ОБОЗНАЧЕНИЕ
- •ГЕОМЕТРИЧЕСКАЯ ИНТЕРПРЕТАЦИЯ ПРЕДЕЛА ФУНКЦИИ
- •ОПРЕДЕЛЕНИЕ ПРЕДЕЛА ФУНКЦИИ ПО ГЕЙНЕ ДАТЬ САМОСТОЯТЕЛЬНО
- •ОДНОСТОРОННИЕ ПРЕДЕЛЫ
- •ОДНОСТОРОННИЕ ПРЕДЕЛЫ
- •ОПРЕДЕЛЕНИЕ
- •ОДНОСТОРОННИЕ
- •БЕСКОНЕЧНО БОЛЬШИЕ ПРЕДЕЛЬНЫЕ ЗНАЧЕНИЯ ФУНКЦИИ
- •БЕСКОНЕЧНО БОЛЬШИЕ ПРЕДЕЛЬНЫЕ ЗНАЧЕНИЯ ФУНКЦИИ
- •САМОСТОЯТЕЛЬНО ДАТЬ ОПРЕДЕЛЕНИЕ И ГЕОМЕТРИЧЕСКУЮ ИНТЕРПРЕТАЦИЮ ТОГО, ЧТО
- •ПРЕДЕЛ ФУНКЦИИ НА БЕСКОНЕЧНОСТИ
- •ПРЕДЕЛ ФУНКЦИИ НА БЕСКОНЕЧНОСТИ
- •ГЕОМЕТРИЧЕСКИЙ СМЫСЛ ПРЕДЕЛА ФУНКЦИИ НА БЕСКОНЕЧНОСТИ
- •САМОСТОЯТЕЛЬНО
- •БЕСКОНЕЧНО МАЛЫЕ И БЕСКОНЕЧНО БОЛЬШИЕ ФУНКЦИИ. ОГРАНИЧЕННЫЕ ФУНКЦИИ
- •БЕСКОНЕЧНО МАЛЫЕ И БЕСКОНЕЧНО БОЛЬШИЕ ФУНКЦИИ
- •ПРИМЕРЫ БЕСКОНЕЧНО МАЛЫХ И БЕСКОНЕЧНО БОЛЬШИХ ФУНКЦИЙ
- •ОГРАНИЧЕННАЯ ФУНКЦИЯ
- •ОГРАНИЧЕННАЯ
- •ОСНОВНЫЕ СВОЙСТВА ПРЕДЕЛОВ ФУНКЦИЙ
- •ОСНОВНЫЕ СВОЙСТВА ПРЕДЕЛОВ ФУНКЦИЙ
- •ОСНОВНЫЕ СВОЙСТВА ПРЕДЕЛОВ ФУНКЦИЙ
- •ЛЕКЦИЯ
- •ТЕОРЕМА
- •ПРИМЕРЫ
- •ЗАМЕЧАТЕЛЬНЫ Е ПРЕДЕЛЫ
- •ПЕРВЫЙ ЗАМЕЧАТЕЛЬНЫЙ ПРЕДЕЛ
- •ПРИМЕР
- •ВТОРОЙ ЗАМЕЧАТЕЛЬНЫЙ ПРЕДЕЛ
- •ВТОРОЙ ЗАМЕЧАТЕЛЬНЫЙ ПРЕДЕЛ
- •ПРИМЕР
- •ВЫЧИСЛЕНИЕ
- •ТЕХНИКА ВЫЧИСЛЕНИЯ ПРЕДЕЛОВ
- •ПРЕДЕЛ ЦЕЛОЙ РАЦИОНАЛЬНОЙ ФУНКЦИИ
- •ТЕХНИКА ВЫЧИСЛЕНИЯ ПРЕДЕЛОВ
- •ПРЕДЕЛ ДРОБНО- РАЦИОНАЛЬНОЙ ФУНКЦИИ
- •ВЫЧИСЛЕНИЕ ПРЕДЕЛОВ
- •ПРИМЕР РАСКРЫТИЯ НЕОПРЕДЕЛЕННОСТИ ВИДА
- •ПРИМЕР РАСКРЫТИЯ НЕОПРЕДЕЛЕННОСТИ ВИДА
- •РАСКРЫТИЕ
- •ТЕХНИКА ВЫЧИСЛЕНИЯ ПРЕДЕЛОВ
- •ПРИМЕР РАСКРЫТИЯ НЕОПРЕДЕЛЕННОСТИ ВИДА 0/0
- •ТЕХНИКА ВЫЧИСЛЕНИЯ ПРЕДЕЛОВ
- •ПРИМЕР РАСКРЫТИЯ НЕОПРЕДЕЛЕННОСТИ ВИДА 0/0
- •СРАВНЕНИЕ
- •СРАВНЕНИЕ БЕСКОНЕЧНО МАЛЫХ
- •ЭКВИВАЛЕНТНЫЕ БЕСКОНЕЧНО МАЛЫЕ
- •СРАВНЕНИЕ БЕСКОНЕЧНО МАЛЫХ
- •СРАВНЕНИЕ БЕСКОНЕЧНО МАЛЫХ
- •СРАВНЕНИЕ БЕСКОНЕЧНО МАЛЫХ
- •ТАБЛИЦА ЭКВИВАЛЕНТНЫХ БЕСКОНЕЧНО МАЛЫХ
- •НЕПРЕРЫВНОСТЬ ФУНКЦИИ. ТОЧКИ РАЗРЫВА И ИХ КЛАССИФИКАЦИЯ
- •ЛЕКЦИЯ №10
- •РАЗЛИЧНЫЕ
- •ОПРЕДЕЛЕНИЕ
- •ЗАМЕЧАНИЕ
- •ОПРЕДЕЛЕНИЕ
- •ОПРЕДЕЛЕНИЕ
- •ОПРЕДЕЛЕНИЯ
- •ДЕЙСТВИЯ НАД НЕПРЕРЫВНЫМИ ФУНКЦИЯМИ. НЕПРЕРЫВНОСТЬ ЭЛЕМЕНТАРНЫХ ФУНКЦИЙ
- •ТЕОРЕМЫ
- •ПРИМЕРЫ
- •ПРИМЕРЫ
- •СВОЙСТВА ФУНКЦИЙ НЕПРЕРЫВНЫХ НА ОТРЕЗКЕ
- •Свойства функций непрерывных на
- •СВОЙСТВА ФУНКЦИЙ НЕПРЕРЫВНЫХ НА ОТРЕЗКЕ
- •ТОЧКИ РАЗРЫВА И ИХ КЛАССИФИКАЦИЯ
- •1. ТОЧКИ РАЗРЫВА ПЕРВОГО РОДА
- •2. ТОЧКИ РАЗРЫВА ВТОРОГО РОДА
- •2.1. ПРОИЗВОДНАЯ И ДИФФЕРЕНЦИАЛ
- •2.1.1. ОПРЕДЕЛЕНИЕ ПРОИЗВОДНОЙ, ЕЕ ФИЗИЧЕСКИЙ И ГЕОМЕТРИЧЕСКИЙ СМЫСЛ
- •ОПРЕДЕЛЕНИЕ ПРОИЗВОДНОЙ
- •ОПРЕДЕЛЕНИЕ ПРОИЗВОДНОЙ
- •ОПРЕДЕЛЕНИЕ
- •ОПРЕДЕЛЕНИЕ ПРОИЗВОДНОЙ
- •ТАБЛИЦА ПРОИЗВОДНЫХ ОСНОВНЫХ ЭЛЕМЕНТАРНЫХ ФУНКЦИЙ
- •СВЯЗЬ МЕЖДУ ДИФФЕРЕНЦИРУЕМОСТЬЮ И НЕПРЕРЫВНОСТЬЮ ФУНКЦИИ
- •ГЕОМЕТРИЧЕСКИЙ СМЫСЛ ПРОИЗВОДНОЙ ФУНКЦИИ
- •Геометрический смысл производной
- •ЛЕКЦИЯ №11
- •Геометрический смысл производной
- •ГЕОМЕТРИЧЕСКИЙ СМЫСЛ ПРОИЗВОДНОЙ
- •Касательная и нормаль
- •ЗАДАЧИ, ПРИВОДЯЩИЕ К ПОНЯТИЮ ПРОИЗВОДНОЙ
- •ЗАДАЧА
- •МЕХАНИЧЕСКИЙ СМЫСЛ ПРОИЗВОДНОЙ
- •Дифференциальное исчисление
- •Физический смысл производной
- •Правила дифференцирования
- •ОСНОВНЫЕ ПРАВИЛА ДИФФЕРЕНЦИРОВАНИЯ
- •ТАБЛИЦА ПРОИЗВОДНЫХ ОСНОВНЫХ ЭЛЕМЕНТАРНЫХ ФУНКЦИЙ
- •ПРИМЕРЫ НАХОЖДЕНИЯ ПРОИЗВОДНЫХ
- •ПРИМЕР
- •ПРИМЕР НАХОЖДЕНИЯ ПРОИЗВОДНОЙ
- •ПРОИЗВОДНАЯ ОБРАТНОЙ ФУНКЦИИ
- •ПРИМЕР
- •ДОКАЗАТЬ
- •ПРОИЗВОДНАЯ СЛОЖНОЙ ФУНКЦИИ
- •ЗАМЕЧАНИЕ
- •ПРОИЗВОДНЫЕ СЛОЖНЫХ ФУНКЦИЙ
- •ПРИМЕРЫ НАХОЖДЕНИЯ ПРОИЗВОДНЫХ СЛОЖНЫХ ФУНКЦИЙ
- •ПРОИЗВОДНАЯ СЛОЖНОЙ ФУНКЦИИ
- •ДИФФЕРЕНЦИРОВАНИЕ СЛОЖНЫХ ЛОГАРИФМИЧЕСКИХ ФУНКЦИЙ
- •ДИФФЕРЕНЦИРОВАНИЕ СЛОЖНЫХ ПОКАЗАТЕЛЬНЫХ ФУНКЦИЙ
- •ЛЕКЦИЯ №12
- •ЛОГАРИФМИЧЕСКОЕ
- •ЛОГАРИФМИЧЕСКОЕ
- •ЛОГАРИФМИЧЕСКОЕ
- •ЗАМЕЧАНИЕ
- •ПРОИЗВОДНАЯ ПОКАЗАТЕЛЬНО- СТЕПЕННОЙ ФУНКЦИИ
- •ПРОИЗВОДНАЯ ПОКАЗАТЕЛЬНО- СТЕПЕННОЙ ФУНКЦИИ
- •ПРОИЗВОДНЫЕ ВЫСШИХ ПОРЯДКОВ
- •ПРОИЗВОДНЫЕ ВЫСШИХ ПОРЯДКОВ
- •ПРОИЗВОДНЫЕ ВЫСШИХ ПОРЯДКОВ ФОРМУЛА ЛЕЙБНИЦА
- •ПРИМЕР
- •ДИФФЕРЕНЦИРОВАНИЕ НЕЯВНЫХ ФУНКЦИЙ
- •ПАРАМЕТРИЧЕСКОЕ ЗАДАНИЕ ФУНКЦИЙ
- •ДИФФЕРЕНЦИРОВАНИЕ ФУНКЦИЙ, ЗАДАННЫХ ПАРАМЕТРИЧЕСКИ
- •ДИФФЕРЕНЦИРОВАНИЕ ФУНКЦИЙ, ЗАДАННЫХ ПАРАМЕТРИЧЕСКИ
- •ПОВТОРНОЕ ДИФФЕРЕНЦИРОВАНИЕ ФУНКЦИЙ, ЗАДАННЫХ ПАРАМЕТРИЧЕСКИ
- •ПОВТОРНОЕ ДИФФЕРЕНЦИРОВАНИЕ ФУНКЦИЙ, ЗАДАННЫХ ПАРАМЕТРИЧЕСКИ
- •ДИФФЕРЕНЦИАЛ ФУНКЦИИ
- •ОПРЕДЕЛЕНИЕ ДИФФЕРЕНЦИАЛА ФУНКЦИИ
- •ДИФФЕРЕНЦИАЛ ФУНКЦИИ
- •ПРИМЕР
- •ПРИМЕР
- •ОПРЕДЕЛЕНИЕ
- •ДИФФЕРЕНЦИАЛ ФУНКЦИИ
- •ДИФФЕРЕНЦИАЛ
- •ДИФФЕРЕНЦИАЛ
- •ДИФФЕРЕНЦИАЛ ФУНКЦИИ. ПРИМЕРЫ
- •ДИФФЕРЕНЦИАЛ ФУНКЦИИ. ПРИМЕР
- •ИНВАРИАНТНОСТЬ ФОРМЫ ПЕРВОГО ДИФФЕРЕНЦИАЛА
- •ДИФФЕРЕНЦИАЛЫ ВЫСШИХ ПОРЯДКОВ
- •ДИФФЕРЕНЦИАЛЫ ВЫСШИХ ПОРЯДКОВ
- •ДИФФЕРЕНЦИАЛЫ ВЫСШИХ ПОРЯДКОВ
- •ДИФФЕРЕНЦИАЛЫ ВЫСШИХ ПОРЯДКОВ
- •ДИФФЕРЕНЦИАЛЫ ВЫСШИХ ПОРЯДКОВ
- •ЗАМЕЧАНИЕ
- •2.2. ПРИМЕНЕНИЕ ДИФФЕРЕНЦИАЛЬНОГО ИСЧИСЛЕНИЯ К ИССЛЕДОВАНИЮ ФУНКЦИЙ
- •2.2.1. ОСНОВНЫЕ ТЕОРЕМЫ ДИФФЕРЕНЦИАЛЬНОГО ИСЧИСЛЕНИЯ
- •ОСНОВНЫЕ ТЕОРЕМЫ ДИФФЕРЕНЦИАЛЬНОГО ИСЧИСЛЕНИЯ
- •ГЕОМЕТРИЧЕСКИЙ СМЫСЛ теоремы Лагранжа.
- •ФОРМУЛА КОШИ
- •2.2.2. РАСКРЫТИЕ НЕОПРЕДЕЛЕННОСТЕ
- •РАСКРЫТИЕ НЕОПРЕДЕЛЕННОСТЕЙ ПО ПРАВИЛУ ЛОПИТАЛЯ
- •ПРАВИЛО ЛОПИТАЛЯ
- •ПРАВИЛО ЛОПИТАЛЯ
- •ЗАМЕЧАНИЯ
- •ПРАВИЛО ЛОПИТАЛЯ
- •ТЕМА1.3. ВЫЧИСЛЕНИЕ ПРЕДЕЛОВ. РАСКРЫТИЕ НЕОПРЕДЕЛЕННОСТЕЙ
- •ВЫЧИСЛЕНИЕ
- •ТЕХНИКА ВЫЧИСЛЕНИЯ ПРЕДЕЛОВ
- •ТЕХНИКА ВЫЧИСЛЕНИЯ ПРЕДЕЛОВ
- •ПРЕДЕЛ ЦЕЛОЙ РАЦИОНАЛЬНОЙ ФУНКЦИИ
- •ТЕХНИКА ВЫЧИСЛЕНИЯ ПРЕДЕЛОВ
- •ПРИМЕР ВЫЧИСЛЕНИЯ ПРЕДЕЛА ДРОБНО-РАЦИОНАЛЬНОЙ ФУНКЦИИ
- •ВЫЧИСЛИТЬ ПРЕДЕЛ ДРОБНО- РАЦИОНАЛЬНОЙ ФУНКЦИИ (ДОМА)
- •ВЫЧИСЛЕНИЕ ПРЕДЕЛОВ
- •ВЫЧИСЛЕНИЕ ПРЕДЕЛОВ
- •РАСКРЫТИЕ
- •ТЕХНИКА ВЫЧИСЛЕНИЯ ПРЕДЕЛОВ
- •ПРИМЕР РАСКРЫТИЯ НЕОПРЕДЕЛЕННОСТИ ВИДА 0/0
- •ПРИМЕР РАСКРЫТИЯ НЕОПРЕДЕЛЕННОСТИ ВИДА 0/0
- •ПРИМЕР РАСКРЫТИЯ НЕОПРЕДЕЛЕННОСТИ ВИДА 0/0
- •ПРИМЕР РАСКРЫТИЯ НЕОПРЕДЕЛЕННОСТИ ВИДА 0/0
- •ПРИМЕР РАСКРЫТИЯ НЕОПРЕДЕЛЕННОСТИ ВИДА 0/0 (ДОМА)
- •ПРИМЕР РАСКРЫТИЯ НЕОПРЕДЕЛЕННОСТИ ВИДА 0/0
- •ТЕХНИКА ВЫЧИСЛЕНИЯ ПРЕДЕЛОВ
- •ПРИМЕР РАСКРЫТИЯ НЕОПРЕДЕЛЕННОСТИ ВИДА 0/0
- •ПРИМЕР РАСКРЫТИЯ НЕОПРЕДЕЛЕННОСТИ ВИДА 0/0
- •ТЕХНИКА ВЫЧИСЛЕНИЯ ПРЕДЕЛОВ
- •ТЕХНИКА ВЫЧИСЛЕНИЯ ПРЕДЕЛОВ
- •ПРИМЕР
- •ТЕХНИКА ВЫЧИСЛЕНИЯ ПРЕДЕЛОВ
- •ПРИМЕРЫ
- •ПРИМЕР
- •ПРИМЕР РАСКРЫТИЯ НЕОПРЕДЕЛЕННОСТИ ВИДА 0/0
- •СПОСОБЫ
- •ПРИМЕР
- •ПРИМЕР
- •РАСКРЫТИЕ НЕОПРЕДЕЛЕННОСТИ
- •ПРИМЕР
- •РАСКРЫТИЕ НЕОПРЕДЕЛЕННОСТИ
- •ПРИМЕР
- •РАСКРЫТИЕ НЕОПРЕДЕЛЕННОСТИ МЕТОДОМ ВЫДЕЛЕНИЯ ГЛАВНОЙ ЧАСТИ БЕСКОНЕЧНО БОЛЬШОЙ ВЕЛИЧИНЫ
- •РАСКРЫТИЕ
- •РАСКРЫТИЕ НЕОПРЕДЕЛЕННОСТИ
- •РАСКРЫТИЕ НЕОПРЕДЕЛЕННОСТИ
- •РАСКРЫТИЕ
- •РАСКРЫТИЕ
- •РАСКРЫТИЕ НЕОПРЕДЕЛЕННОСТИ
- •РАСКРЫТИЕ НЕОПРЕДЕЛЕННОСТИ
- •РАСКРЫТИЕ НЕОПРЕДЕЛЕННОСТИ
- •РАСКРЫТИЕ
- •РАСКРЫТИЕ НЕОПРЕДЕЛЕННОСТИ
- •РАСКРЫТИЕ
- •РАСКРЫТИЕ НЕОПРЕДЕЛЕННОСТИ
- •ПРИМЕР РАСКРЫТИЯ НЕОПРЕДЕЛЕННОСТИ
- •ПРИМЕР (ДОМА)
- •РАСКРЫТИЕ НЕОПРЕДЕЛЕННОСТИ ВИДА
- •РАСКРЫТИЕ НЕОПРЕДЕЛЕННОСТИ ВИДА
- •РАСКРЫТИЕ НЕОПРЕДЕЛЕННОСТИ ВИДА
- •ПРИМЕРЫ РАСКРЫТИЯ НЕОПРЕДЕЛЕННОСТЕЙ С ИСПОЛЬЗОВАНИЕМ ЭКВИВАЛЕНТНЫХ БЕСКОНЕЧНО МАЛЫХ
- •ТАБЛИЦА ЭКВИВАЛЕНТНЫХ БЕСКОНЕЧНО МАЛЫХ
- •ЭКВИВАЛЕНТНЫЕ БЕСКОНЕЧНО МАЛЫЕ
- •ЭКВИВАЛЕНТНЫЕ БЕСКОНЕЧНО МАЛЫЕ
- •ЭКВИВАЛЕНТНЫЕ БЕСКОНЕЧНО МАЛЫЕ
- •ЭКВИВАЛЕНТНЫЕ БЕСКОНЕЧНО МАЛЫЕ
- •ЭКВИВАЛЕНТНЫЕ БЕСКОНЕЧНО
- •ПРИМЕР РАСКРЫТИЯ НЕОПРЕДЕЛЕННОСТИ ВИДА 0/0
- •ПРИМЕРЫ РАСКРЫТИЯ НЕОПРЕДЕЛЕННОСТЕЙ ВИДА 0/0
- •ПРИМЕР РАСКРЫТИЯ НЕОПРЕДЕЛЕННОСТИ ВИДА 0/0
- •ПРИМЕР РАСКРЫТИЯ НЕОПРЕДЕЛЕННОСТИ ВИДА 0/0
- •ПРИМЕР РАСКРЫТИЯ НЕОПРЕДЕЛЕННОСТИ ВИДА 0/0
- •ПРИМЕР
- •Вычислить предел функции.
- •ТЕМА 1.3. НЕПРЕРЫВНОСТЬ ФУНКЦИИ. ТОЧКИ РАЗРЫВА И ИХ КЛАССИФИКАЦИЯ
- •ОПРЕДЕЛЕНИЕ 1
- •ОПРЕДЕЛЕНИЕ 2
- •ЗАМЕЧАНИЕ
- •ОПРЕДЕЛЕНИЕ 3
- •ДЕЙСТВИЯ НАД НЕПРЕРЫВНЫМИ ФУНКЦИЯМИ. НЕПРЕРЫВНОСТЬ ЭЛЕМЕНТАРНЫХ ФУНКЦИЙ
- •СВОЙСТВА НЕПРЕРЫВНЫХ
- •СВОЙСТВА НЕПРЕРЫВНЫХ ФУНКЦИЙ
- •ПРИМЕРЫ №1-№2
- •ПРИМЕР №3
- •СВОЙСТВА ФУНКЦИЙ НЕПРЕРЫВНЫХ НА ОТРЕЗКЕ
- •ПРИМЕР №4
- •Свойства функций непрерывных на
- •СВОЙСТВА ФУНКЦИЙ НЕПРЕРЫВНЫХ НА ОТРЕЗКЕ
- •ТОЧКИ РАЗРЫВА И ИХ КЛАССИФИКАЦИЯ
- •1. ТОЧКИ РАЗРЫВА ПЕРВОГО РОДА
- •2. ТОЧКИ РАЗРЫВА ВТОРОГО РОДА
- •ПРИМЕРЫ
- •ПРИМЕР №5
- •ПРИМЕР №5 (ПРОДОЛЖЕНИЕ)
- •ПРИМЕР 6
- •(ПРОДОЛЖЕНИЕ)
- •ПРИМЕР № 7
- •СПАСИБО ЗА ВНИМАНИЕ
- •Производная функции
- •СФизическийгеометрическойсмысл точки зрения дифференциру-емость означает,производнойчто к графику функции в данной точке можно
- •Геометрический смысл производной
- •Касательная и нормаль
- •Односторонние производные
- •Теорема 1. (Необходимое и достаточное условие существования производной в точке)
- •Правила
- •Правила дифференцирования
- •Правила дифференцирования
- •Дифференциал функции
- •Геометрический смысл дифференциала
- •Правила
- •Таблица производных
- •РАЗЛИЧНЫЕ ОПРЕДЕЛЕНИЯ
- •АЛГЕБРАИЧЕСКИЕ И ТРАНСЦЕНДЕНТНЫЕ
- •ОПРЕДЕЛЕНИЕ. Элементарной функцией
- •СПОСОБЫ ЗАДАНИЯ ФУНКЦИИ
- •СПОСОБЫ ЗАДАНИЯ ФУНКЦИИ
- •ПОНЯТИЕ ФУНКЦИИ
- •ЗАДАЧНИКИ С РЕШЕНИЯМИ
- •ОСНОВНЫЕ ТЕОРЕМЫ О ПРЕДЕЛАХ ПЕРЕМЕННЫХ
- •1.2.1. ПОНЯТИЕ ПРЕДЕЛА ФУНКЦИИ
- •СВОЙСТВА БЕСКОНЕЧНО МАЛЫХ ВЕЛИЧИН
- •СВОЙСТВА БЕСКОНЕЧНО БОЛЬШИХ ВЕЛИЧИН
- •СВЯЗЬ МЕЖДУ БЕСКОНЕЧНО МАЛОЙ И БЕСКОНЕЧНО БОЛЬШОЙ ВЕЛИЧИНАМИ
- •ЗАМЕЧАТЕЛЬНЫЙ ПРЕДЕЛ И ЕГО СЛЕДСТВИЯ
- •ЗАМЕЧАТЕЛЬНЫЙ ПРЕДЕЛ И ЕГО СЛЕДСТВИЯ
- •ОПРЕДЕЛЕНИЕ ЛЕВОСТОРОННЕЙ И ПРАВОСТОРОННЕЙ ПРЕДЕЛЬНОЙ ТОЧКИ ДАТЬ САМОСТОЯТЕЛЬНО
- •ОПРЕДЕЛЕНИЕ
- •ОПРЕДЕЛЕНИЕ ПРЕДЕЛА ФУНКЦИИ ПО ГЕЙНЕ( НА ЯЗЫКЕ ПОСЛЕДОВАТЕЛЬНОСТЕЙ)
- •ОПРЕДЕЛЕНИЕ
- •ОДНОСТОРОННИЕ ПРЕДЕЛЫ
- •ЗАМЕЧАТЕЛЬНЫЙ ПРЕДЕЛ И ЕГО СЛЕДСТВИЯ
- •ПРИМЕРЫ
- •ЗАМЕЧАТЕЛЬНЫЙ ПРЕДЕЛ И ЕГО СЛЕДСТВИЯ
- •ДИФФЕРЕНЦИРОВАНИЕ ФУНКЦИЙ, ЗАДАННЫХ ПАРАМЕТРИЧЕСКИ
- •ТЕХНИКА ВЫЧИСЛЕНИЯ ПРЕДЕЛОВ
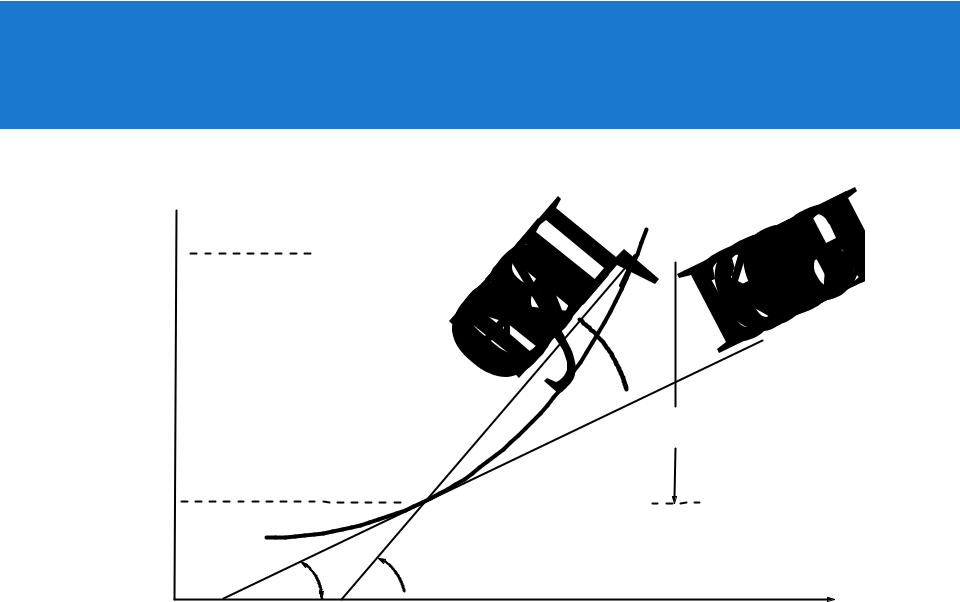
Геометрический смысл производной
 f(x0+x)
f(x0+x)


























 f(x)осьвращенияMx
f(x)осьвращенияMx





 f(x0+x)-f(x0)
f(x0+x)-f(x0)
0 '0

 x
x




 x+
x+ x
x
0 0
165

ГЕОМЕТРИЧЕСКИЙ СМЫСЛ ПРОИЗВОДНОЙ
166
167

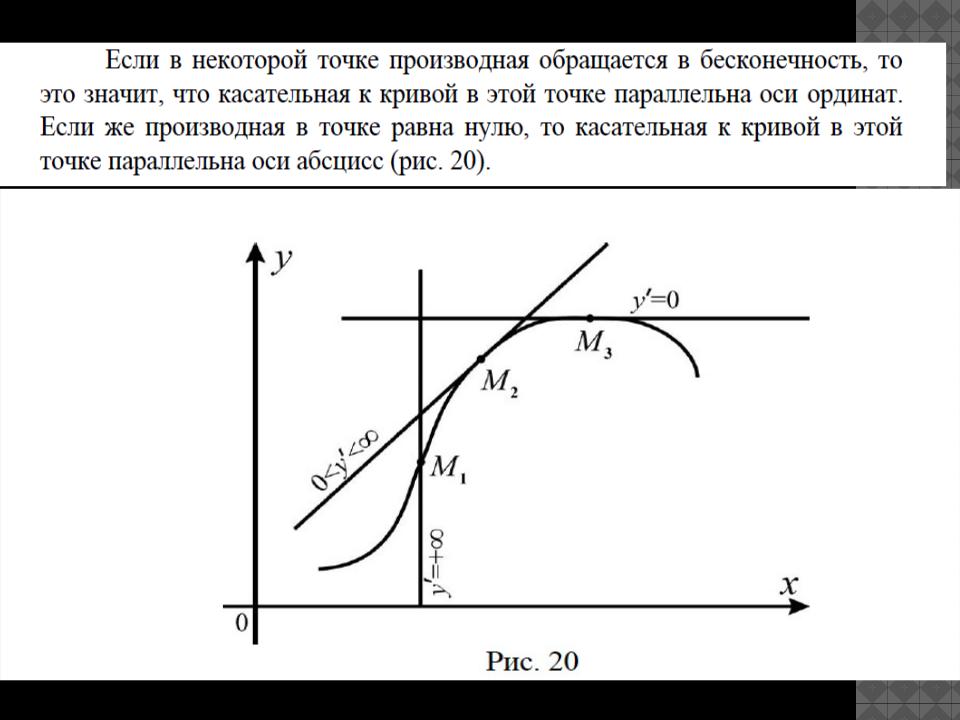
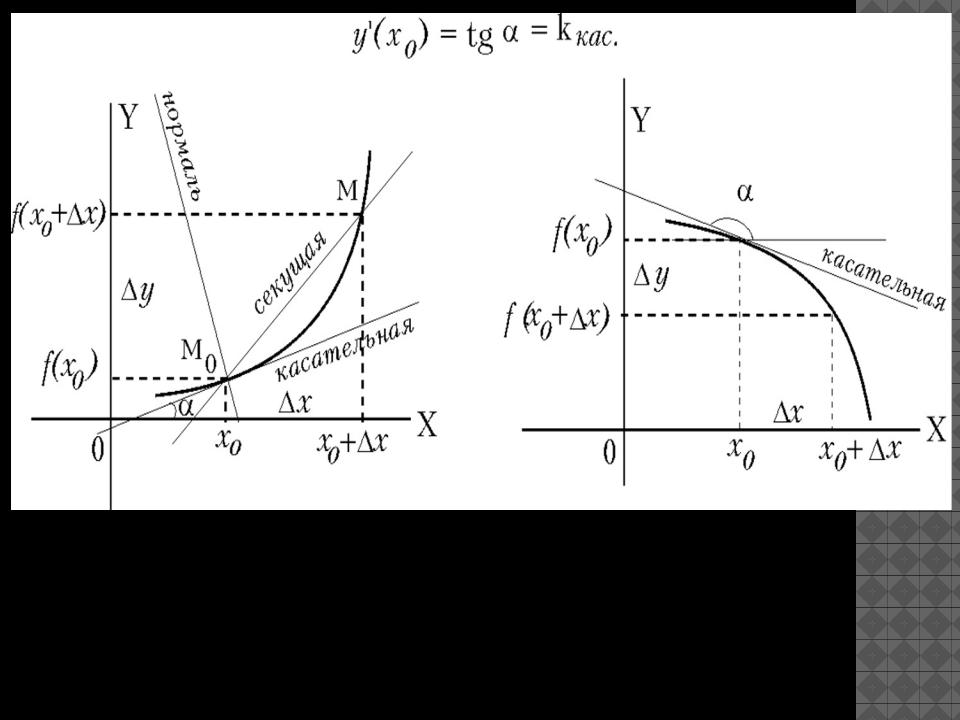
Касательная и нормаль
Определение. Касательной к графику функции в точке
М0(x0, y0 ) назовем предельное положение секущей М0М,
когда точка М, двигаясь вдоль кривой, стремится к совпадению с точкой М0.
|
Уравнение касательной к графику функции в точке М0(x0, |
y0): |
y y0 f (x0 )(x. x0 ) |
Прямая, проведенная через точку касания, перпендикулярно касательной к графику функции, называется нормалью.
Уравнение нормали к графику функции в точке М0(x0, y0): |
||||
y y0 |
1 |
(x |
x0 ) |
|
f (x0 ) |
||||
168 |
|
|
||
|
|
|
||
y y0 |
|
1 |
(x |
x0 ) |
|
|
|
||||
|
|
||||
|
f |
|
|
y y0 f (x0 )(x x0 ) |
|
|
(x0 ) |
|
|
|
169

ЗАДАЧИ, ПРИВОДЯЩИЕ К ПОНЯТИЮ ПРОИЗВОДНОЙ
170

ЗАДАЧА
171

172

МЕХАНИЧЕСКИЙ СМЫСЛ ПРОИЗВОДНОЙ
173

Дифференциальное исчисление
Задача . Пусть (t) есть количество вещества прореагировавшего за время t. В момент времени t+ t количество вещества будет (t+ t), т.е. за промежуток времени (t, t+ t) количество прореагировавшего вещества
= (t + t) – (t).
Средняя скорость химической реакции за интервал времени t будет равна / t. Чтобы найти скорость химической реакции в данный момент времени t надо устремить t к нулю, то есть
v(t) lim |
(t t) (t) |
(t) |
t 0 |
t |
|
Таким образом, производная от количества прореагировавшего вещества определяет скорость химической реакции.
174
