
- •111Equation Chapter 1 Section 1министерство образования и науки российской федерации
- •«Национальный исследовательский
- •Матанализ 3
- •Аннотация
- •Матанализ 3
- •130102 «Технология геологической разведки»,022000 «Экология и природопользование»
- •Отпечатано в Издательстве тпу в полном соответствиис качеством предоставленного оригинал-макета
- •I. Интегральное исчисление функции одной переменной Неопределенный интеграл
- •Определенный интеграл
- •II. Дифференциальные уравнения
- •Основные свойства неопределенного интеграла
- •Полезно помнить таблицу дифференциалов:
- •Непосредственное интегрирование
- •Метод подстановки
- •Метод интегрирования по частям
- •Интегрирование рациональных дробей
- •Алгоритм интегрирования рациональной дроби
- •Примеры интегрирования рациональных функций
- •Интегрирование тригонометрических функций
- •Интегрирование некоторых иррациональных функций
- •Определенный интеграл
- •Рассмотрим частные случаи
- •Теорема существования определенного интеграла
- •Интеграл расходится, т. К. Предел не существует. Пусть теперь функция непрерывна на интервалеи. Если существует конечный предел, то его называют несобственным интегралом второго рода и обозначают
- •Функция определена на , и то есть мы имеем дело с несобственным интегралом от функции с бесконечным разрывом. Таким образом,
- •Некоторые приложения определенного интеграла
- •1. Вычисление площади плоской фигуры
- •2. Длина дуги кривой
- •3. Объем тела
- •II. Дифференциальные уравнения Дифференциальные уравнения первого порядка
- •1. Уравнения с разделяющимися переменными
- •Умножим обе части уравнения на 2
- •2. Уравнения, приводящиеся к уравнениям с разделяющимися переменными Уравнения вида
- •3. Однородные уравнения
- •Разделим переменные
- •4. Линейные дифференциальные уравнения первого порядка
- •Решение линейного уравнения методом подстановки
- •5. Уравнение Бернулли
- •Преобразованное уравнение (26) является линейным относительно и. Решив его, найдем общий интеграл уравнения (26). Далее, подставив , получим общее решение уравнения Бернулли (24).
- •6. Уравнение в полных дифференциалах
- •Нахождение общего решения уравнения
- •III. Числовые ряды Если каждому натуральному числу поставлено в соответствие некоторое вполне определенное число, то говорят, что задана числовая последовательность.
- •1. Интегральный признак Коши
- •Следовательно, обобщенный гармонический ряд сходится прии расходится при.
- •Решение. Составим ряд из модулей Получим гармонический ряд, который расходится. Проверим условия признака Лейбница:
- •IV. Функциональные ряды
- •V. Степенные ряды
- •1. Теорема Абеля
- •Решение.
- •3. Методы разложения функций в ряд Тейлора
- •Решение. Воспользуемся формулой суммы бесконечно убывающей геометрической прогрессии
- •Данное разложение имеет место для всех . Варианты заданий для контрольной работы № 6
- •Учебно-методическое обеспечение дисциплины Литература обязательная
3. Объем тела
Пусть
требуется найти объем V
тела, причем известна площадь
 сечения
тела, плоскостями, перпендикулярными
к оси
сечения
тела, плоскостями, перпендикулярными
к оси
 то
то
 (14)
(14)
Пример
34.
Найти объем эллипсоида

Рассекая
эллипсоид плоскостью, параллельной
плоскости
 и на расстоянии
и на расстоянии от неё
от неё получим эллипс
получим эллипс

Площадь
этого эллипса равна

поэтому

4. Объем тела вращения
Объем
тела, полученного вращением кривой
вокруг оси ох
(см.
рис. 11), определяется интегралом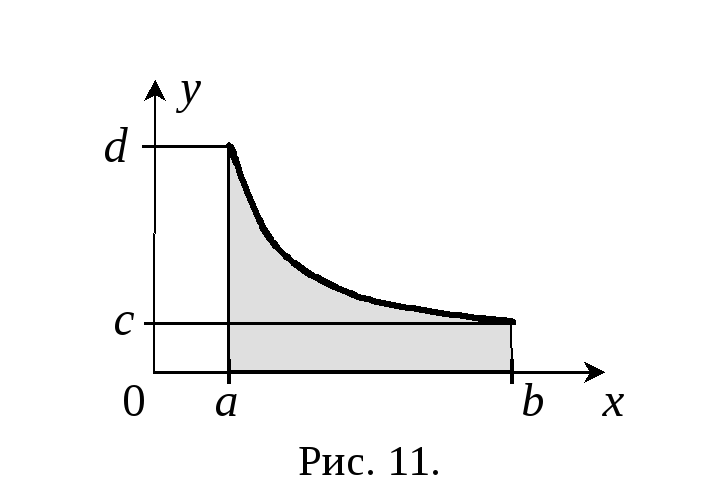
 (15)
(15)
Аналогично, вокруг оси 0у.
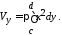 (16)
(16)
Пример 35. Найти объем тела, образованного вращением фигуры, ограниченной линиями
 вокруг
оси
вокруг
оси
 .
.

Находим

Варианты заданий для контрольной работы № 3
Задание 1. Найти неопределенные интегралы.
В задачах 1 и 2 результат проверить дифференцированием.
В задачах 3 и 4 вычислить интегралы по формуле интегрирования по частям.
В задачах 5 и 6 проинтегрировать рациональные функции.
В задачах 7 и 8 найти интегралы от тригонометрических функций.
В задачах 9 и 10 вычислить интегралы, используя подходящую подстановку.
Вариант 1
1. ;
2.
;
2. ; 3.
; 3. ;
4.
;
4. ;
;
5.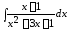 ;
6.
;
6. ;
7.
;
7. ;
;
8. ;
9.
;
9. ; 10.
; 10. .
.
Вариант 2
1. ;
2.
;
2. ;
3.
;
3. ;
4.
;
4. ;
;
5. ; 6.
; 6. ; 7.
; 7. ;
;
8. ; 9.
; 9.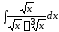 ; 10.
; 10. .
.
Вариант 3
1. ; 2.
; 2. ; 3.
; 3. ; 4.
; 4. ;
;
5. ; 6.
; 6. ; 7.
; 7. ;
;
8. ; 9.
; 9. ; 10.
; 10. .
.
Вариант 4
1. ; 2.
; 2. 3.
3. 4.
4.
 ;
;
5. ; 6.
; 6.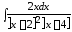 ; 7.
; 7. ;
;
8. ; 9.
; 9. ; 10.
; 10. .
.
Вариант 5
1.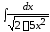 ; 2.
; 2.
 ; 3.
; 3. ; 4.
; 4.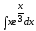 ;
;
5. ; 6.
; 6. ; 7.
; 7. ;
;
8. ; 9.
; 9. ; 10.
; 10.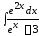 .
.
Вариант 6
1. 2.
2. 3.
3. 4.
4.
5. 6.
6. 7.
7.
8.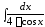 9.
9. 10.
10.
Вариант 7
1. ; 2.
; 2. ; 3.
; 3. ;
4.
;
4. ;
;
5. ; 6.
; 6. ; 7.
; 7. ;
;
8. ; 9.
; 9.
 ; 10.
; 10. .
.
Вариант 8
1. ; 2.
; 2.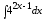 ; 3.
; 3. ; 4.
; 4. ;
;
5. ; 6.
; 6. ; 7.
; 7.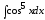 ;
;
8. ; 9.
; 9. ; 10.
; 10. .
.
Вариант 9
1. ; 2.
; 2. ;
3.
;
3. ; 4.
; 4. ;
;
5. ; 6.
; 6. ; 7.
; 7. ;
;
8. ; 9.
; 9. ; 10.
; 10. .
.
Вариант 10
1. ; 2.
; 2. ; 3.
; 3. ; 4.
; 4. ;
;
5. ; 6.
; 6. ; 7.
; 7. ;
;
8. ; 9.
; 9. ; 10.
; 10.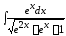
Вариант 11
1. ; 2.
; 2. ;
3.
;
3. ; 4.
; 4. ;
;
5. ; 6.
; 6. ; 7.
; 7. ;
;
8. ; 9.
; 9. ; 10.
; 10. .
.
Вариант 12
1. ; 2.
; 2. ; 3.
; 3. ; 4.
; 4.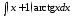 ;
;
5. ; 6.
; 6. ; 7.
; 7. ;
;
8.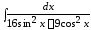 ; 9.
; 9. ; 10.
; 10.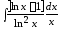 .
.
Вариант 13
1. ; 2.
; 2. ;
3.
;
3. ; 4.
; 4. ;
;
5. ; 6.
; 6. ; 7.
; 7. ;
;
8. ; 9.
; 9. ; 10.
; 10. .
.
Вариант 14
1. ; 2.
; 2. ; 3.
; 3. ; 4.
; 4. ;
;
5. ; 6.
; 6. ; 7.
; 7. ;
;
8. ; 9.
; 9. ; 10.
; 10. .
.
Вариант 15
1.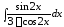 ; 2.
; 2. ; 3.
; 3. ; 4.
; 4. ;
;
5. ; 6.
; 6. ; 7.
; 7. ;
;
8. ; 9.
; 9. ; 10.
; 10. .
.
Вариант 16
1. ; 2.
; 2. ; 3.
; 3. ; 4.
; 4.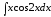 ;
;
5. ; 6.
; 6. ;
7.
;
7. ;
;
8. ; 9.
; 9. ; 10.
; 10. .
.
Вариант 17
1. ;
2.
;
2. ;
3.
;
3. ;
4.
;
4. ;
;
5. ; 6.
; 6. ; 7.
; 7. ;
;
8. ; 9.
; 9. ; 10.
; 10. .
.
Вариант 18
1. ;
2.
;
2. ;
3.
;
3. ; 4.
; 4. ;
;
5. ; 6.
; 6. ; 7.
; 7. ;
;
8.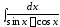 ; 9.
; 9. ; 10.
; 10. .
.
Вариант 19
1. ;
2.
;
2. ;
3.
;
3. ;
4.
;
4. ;
;
5. ; 6.
; 6.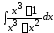 ; 7.
; 7. ;
;
8. ; 9.
; 9. ; 10.
; 10. .
.
Вариант 20
1. ; 2.
; 2.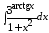 ;
3.
;
3. ;4.
;4. ;
;
5. ; 6.
; 6. ; 7.
; 7.
 ;
;
8. ; 9.
; 9. ; 10.
; 10.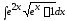 .
.
Задание 2. Вычислить определенный интеграл



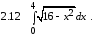






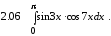









Задание 3. Вычислить несобственный интеграл или показать его расходимость.





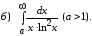











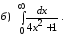

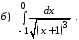




















Задание 4. Вычислить площадь плоской фигуры, ограниченной линиями.

 (вне окружности)
(вне окружности)
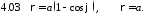

















Задание 5. Вычислить длину дуги кривой.



















 .
.
Задание 6. Вычислить объем тела, образованного вращением вокруг оси 0х кривой, заданной уравнениями.
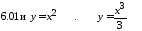






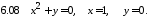


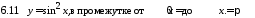










II. Дифференциальные уравнения Дифференциальные уравнения первого порядка
Определение. Соотношения, в которых неизвестные переменные и их функции находятся под знаком производной или дифференциала, называются дифференциальными уравнениями.
Определение.
Дифференциальным уравнением первого
порядка называется уравнение, связывающее
независимую переменную
 ,
искомую функцию
,
искомую функцию и её производную первого порядка
и её производную первого порядка или дифференциалы
или дифференциалы и
и .
.
Дифференциальное уравнение первого порядка имеет вид
 (1)
(1)
Если это уравнение можно разрешить относительно у', то оно примет вид
 (2)
(2)
Основной задачей теории дифференциальных уравнений является нахождение неизвестных функций, определяемых дифференциальными уравнениями
Определение.
Решением дифференциального уравнения
(1) называется функция
 ,
обращающая уравнение в тождество.
,
обращающая уравнение в тождество.
Определение. Общим решением дифференциального уравнения первого порядка называется функция
 ,
(3)
,
(3)
которая зависит от произвольной постоянной с и обращает дифференциальное уравнение (1) в тождество.
Определение. Общее решение
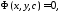 (4)
(4)
заданное в неявном виде, называется общим интегралом этого уравнения.
Определение.
Частным решением дифференциального
уравнения (1) называется функция
 ,
которая получается из общего решения
(3) при определенном числовом значении
,
которая получается из общего решения
(3) при определенном числовом значении .
.
Теорема существования и единственности решения дифференциального уравнения первого порядка.
Пусть
в уравнении (2) функция
 и её частная производная
и её частная производная непрерывны в некоторой области
непрерывны в некоторой области на
плоскости
на
плоскости .
Тогда, какова бы ни была точка
.
Тогда, какова бы ни была точка ,
всегда существует (и при том только
одно) такое решение этого уравнения
,
всегда существует (и при том только
одно) такое решение этого уравнения ,
которое равно
,
которое равно при
при ,
т. к.
,
т. к.
 .
.
Условие,
что
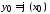 при
при ,
называется начальным условием.
,
называется начальным условием.
Оно записывается в виде
 или
или
 (5)
(5)
Поставим
задачу.
Найти решение
 уравнения (2), удовлетворяющее предыдущей
теореме.
уравнения (2), удовлетворяющее предыдущей
теореме.
Такая задача называется задачей Коши.
Определение. Решение, в каждой точке которого нарушается единственность решения задачи Коши, называется особым.
Замечание.
В некоторых случаях выгодно за искомую
функцию считать переменную
 и записывать уравнение (2) в виде
и записывать уравнение (2) в виде
 где
где
 (6)
(6)
Учитывая,
что
 и
и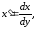 дифференциальные уравнения (1), (2) и (6)
можно записать в форме
дифференциальные уравнения (1), (2) и (6)
можно записать в форме
 (7)
(7)
где
 и
и известные функции.
известные функции.
Пример
1.
Найти общее решение уравнения

Решение.
Так как
 ,
то получим
,
то получим
Тогда
 Интегрируя
обе части уравнения, окончательно
получим
Интегрируя
обе части уравнения, окончательно
получим
Общее
решение данного уравнения образует
семейство кубических парабол, т.к.
 может
принимать любое числовое значение.
может
принимать любое числовое значение.

Рассмотрим частное решение.
Пусть наша кривая проходит через точку М(1,0), см. рис. Подставим координаты точки М в общее решение. Получим
 ,
откуда
,
откуда

Тогда частное решение имеет вид

Геометрическое
толкование дифференциального уравнения
первого порядка заключается в том, что
общее решение (общий интеграл) (4)
представляет собой семейство кривых
на координатной плоскости, зависящее
от одной произвольной постоянной
 .
.
Эти кривые называются интегральными кривыми уравнениями (1), (2).
Частному решению (задачи Коши) соответствует одна кривая этого семейства, проходящая через данную точку плоскости.
Решить дифференциальное уравнение (1) значит:
найти его общее решение (если начальные условия не заданы);
найти частное решение уравнения (1), которое удовлетворяет начальным условиям или, другими словами, решить задачу Коши.
Рассмотрим некоторые типы дифференциальных уравнений первого порядка.
