
- •111Equation Chapter 1 Section 1министерство образования и науки российской федерации
- •«Национальный исследовательский
- •Матанализ 3
- •Аннотация
- •Матанализ 3
- •130102 «Технология геологической разведки»,022000 «Экология и природопользование»
- •Отпечатано в Издательстве тпу в полном соответствиис качеством предоставленного оригинал-макета
- •I. Интегральное исчисление функции одной переменной Неопределенный интеграл
- •Определенный интеграл
- •II. Дифференциальные уравнения
- •Основные свойства неопределенного интеграла
- •Полезно помнить таблицу дифференциалов:
- •Непосредственное интегрирование
- •Метод подстановки
- •Метод интегрирования по частям
- •Интегрирование рациональных дробей
- •Алгоритм интегрирования рациональной дроби
- •Примеры интегрирования рациональных функций
- •Интегрирование тригонометрических функций
- •Интегрирование некоторых иррациональных функций
- •Определенный интеграл
- •Рассмотрим частные случаи
- •Теорема существования определенного интеграла
- •Интеграл расходится, т. К. Предел не существует. Пусть теперь функция непрерывна на интервалеи. Если существует конечный предел, то его называют несобственным интегралом второго рода и обозначают
- •Функция определена на , и то есть мы имеем дело с несобственным интегралом от функции с бесконечным разрывом. Таким образом,
- •Некоторые приложения определенного интеграла
- •1. Вычисление площади плоской фигуры
- •2. Длина дуги кривой
- •3. Объем тела
- •II. Дифференциальные уравнения Дифференциальные уравнения первого порядка
- •1. Уравнения с разделяющимися переменными
- •Умножим обе части уравнения на 2
- •2. Уравнения, приводящиеся к уравнениям с разделяющимися переменными Уравнения вида
- •3. Однородные уравнения
- •Разделим переменные
- •4. Линейные дифференциальные уравнения первого порядка
- •Решение линейного уравнения методом подстановки
- •5. Уравнение Бернулли
- •Преобразованное уравнение (26) является линейным относительно и. Решив его, найдем общий интеграл уравнения (26). Далее, подставив , получим общее решение уравнения Бернулли (24).
- •6. Уравнение в полных дифференциалах
- •Нахождение общего решения уравнения
- •III. Числовые ряды Если каждому натуральному числу поставлено в соответствие некоторое вполне определенное число, то говорят, что задана числовая последовательность.
- •1. Интегральный признак Коши
- •Следовательно, обобщенный гармонический ряд сходится прии расходится при.
- •Решение. Составим ряд из модулей Получим гармонический ряд, который расходится. Проверим условия признака Лейбница:
- •IV. Функциональные ряды
- •V. Степенные ряды
- •1. Теорема Абеля
- •Решение.
- •3. Методы разложения функций в ряд Тейлора
- •Решение. Воспользуемся формулой суммы бесконечно убывающей геометрической прогрессии
- •Данное разложение имеет место для всех . Варианты заданий для контрольной работы № 6
- •Учебно-методическое обеспечение дисциплины Литература обязательная
Интегрирование тригонометрических функций
Рассмотрим несколько видов интегралов от тригонометрических функций.
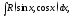 где
где
 − рациональная функция от
− рациональная функция от и
и .
Это означает, что над аргументами
производятся только рациональные
операции: сложение, вычитание, умножение,
деление, возведение в целые степени
(положительные и отрицательные).
Интегралы этого вида приводятся к
рациональной функции от
.
Это означает, что над аргументами
производятся только рациональные
операции: сложение, вычитание, умножение,
деление, возведение в целые степени
(положительные и отрицательные).
Интегралы этого вида приводятся к
рациональной функции от универсальной тригонометрической
подстановкой:
универсальной тригонометрической
подстановкой:



 ,
,
 .
.
Следует
заметить, что, применяя эту подстановку
можно привести любую подынтегральную
функцию
 к рациональной дроби, но иногда получаются
громоздкие дроби, которые трудно
проинтегрировать.
к рациональной дроби, но иногда получаются
громоздкие дроби, которые трудно
проинтегрировать.
Рассмотрим частные случаи, когда можно избежать универсальной подстановки.
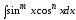 .
.
Где
 и
и – целые положительные числа. Если
– целые положительные числа. Если и
и – четные, то используется тригонометрические
формулы понижения степени,
– четные, то используется тригонометрические
формулы понижения степени,
 ,
,
 .
.
Пример
15.




Если одно из чисел
 или
или – нечетное, или
– нечетное, или и
и – нечетные, то отделяем от нечетной
степени один множитель и делаем замену
– нечетные, то отделяем от нечетной
степени один множитель и делаем замену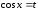 (или
(или )
–
)
– .
.
Пример 16.
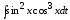 =
= =
= =
= ,
,
где
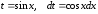
Пример
17.  .
.
Применим универсальную тригонометрическую подстановку:
 ,
,
 ,
, ,
, .
.
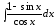
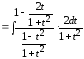


 ;
;
Разложим
дробь
 на простейшие
на простейшие

 ;
;
Откуда
 .
.
Найдем коэффициенты разложения из системы:



 .
.
Проинтегрируем:




 .
.
Если
 и
и – дробные либо целые (отрицательные)
числа и
– дробные либо целые (отрицательные)
числа и – целое отрицательное число, тогда
рекомендуется подстановка
– целое отрицательное число, тогда
рекомендуется подстановка
 ,
, ,
,
или

 ,
, ,
, .
.
Пример
18. 
 ;
;
т.к.

 четное отрицательное число.
четное отрицательное число.
Используем
подстановку
 ,
, ,
,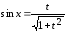 ,
, ;
;


Интегралы вида
 ,
, ,
где
,
где >
> ,
, >0
вычисляются при помощи подстановки
>0
вычисляются при помощи подстановки ,
, и
и ,
, .
.
Пример 19.
 =
=

 ;
;
Т.к.
дробь
 – неправильная, то надо выделить целую
часть дроби, поделив
– неправильная, то надо выделить целую
часть дроби, поделив на
на .
.
 .
.
Интегралы вида


где
 ,
, – действительные числа.
– действительные числа.
Напомним известные тригонометрические формулы:
 ;
;
 ;
;
 .
.
Заменив подынтегральные функции по этим формулам, получим интегралы, которые вычисляются просто.
Пример
20.  =
=
Интегрирование некоторых иррациональных функций
Определение 3. Функция называется алгебраической иррациональной, если над аргументом производится только четыре арифметических действия и действие возведения в рациональную степень.
Метод интегрирования алгебраических иррациональностей состоит в выборе подстановки, которая привела бы подынтегральную функцию к рациональной.
Наиболее часто встречаются иррациональности вида:
 ;
;
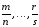 – несократимые дроби.
– несократимые дроби.
Рекомендуется
подстановка:
 ,
где
,
где – наименьшее общее кратное знаменателей
дробей
– наименьшее общее кратное знаменателей
дробей ,
(н.о.к.
,
(н.о.к. ).
).
 ;
;
Подстановка:
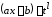 ,
где
,
где н.о.к.
н.о.к. .
.
 .
.
Подстановка:
 ,
где
,
где н.о.к.
н.о.к.  приводит подынтегральную функцию к
рациональному виду.
приводит подынтегральную функцию к
рациональному виду.
 ; Подстановка:
; Подстановка:
 ,
,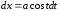 .
. ; Подстановка:
; Подстановка:
 ,
, .
. ; Подстановка:
; Подстановка:
 ,
, .
.
 приводится
к одному из видов в п. II
методом выделения полного квадрата
трехчлена, стоящего под корнем квадратным.
приводится
к одному из видов в п. II
методом выделения полного квадрата
трехчлена, стоящего под корнем квадратным.
Пример
21. 
 ;
;
Наименьшее
общее кратное знаменателей дробей
 ,
, равно 10.
равно 10.
Сделаем
подстановку ,
, ;
;
Тогда
 .
.
 –правильная
рациональная дробь. Разложим ее на
простейшие рациональные дроби, что
рекомендуется проделать самостоятельно.
–правильная
рациональная дробь. Разложим ее на
простейшие рациональные дроби, что
рекомендуется проделать самостоятельно.
Получим:
 =
=
=
 ,
где
,
где
 .
.
Пример
22. 
 ;
;
Сделаем
подстановку, которая приводит
подынтегральную функцию к рациональному
виду:
 ;
;
Найдем
из этого уравнения
 и
и :
:
 ;
;
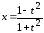 ;
;
 .
.
Тогда
 .
.
Проинтегрируем
правильную рациональную дробь
 ,
разложив ее на простейшие дроби, используя
метод неопределенных коэффициентов.
,
разложив ее на простейшие дроби, используя
метод неопределенных коэффициентов.
Представим интеграл в виде суммы: (рекомендуется выполнить самостоятельно),


 .
.
Возвращаясь
к старой переменной по формуле
 ,
,
получим
 .
.
Пример
23.  ;
Это интеграл типа II.
;
Это интеграл типа II.
Применим
подстановку
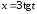 ;
; ;
;
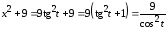 ;
;
тогда
 ;
;
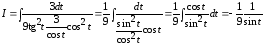 ;
;
Чтобы
вернуться к первоначальной переменной,
выразим
 через
через ;
;
 ;
;
Получим
 ;
;
Пример
24.  ;
Это интеграл типа III.
;
Это интеграл типа III.
Алгоритм вычисления интеграла такого типа аналогичен алгоритму интегрирования рациональной дроби типа III:
 ,
а именно:
,
а именно:
Выделение полного квадрата трехчлена, стоящего в знаменателе;
Введение новой переменной.





Интеграл от дифференциального бинома:
 ,
может быть вычислен в конечном виде
только в следующих случаях:
,
может быть вычислен в конечном виде
только в следующих случаях:
 –целое
число, тогда применима подстановка
–целое
число, тогда применима подстановка
 ,
где
,
где – общий знаменатель дробей
– общий знаменатель дробей и
и .
Или разлагают на сумму по формуле бинома
Ньютона.
.
Или разлагают на сумму по формуле бинома
Ньютона. –целое
число, подстановка
–целое
число, подстановка
 ,
где
,
где – знаменатель дроби
– знаменатель дроби .
. –целое
число, подстановка
–целое
число, подстановка
 ,
где
,
где – знаменатель дроби
– знаменатель дроби .
.
Эти подстановки называются подстановками Чебышева, который доказал, что только в этих случаях дифференциальный бином может быть приведен к рациональному виду и вычислен при помощи элементарных функций.
Пример
25.  ;
;
Запишем
интеграл в виде
 ,
,
где
 ,
, ,
, ,
, .
.
 –не
целое число;
–не
целое число;  – целое число.
– целое число.
В
этом случае применима подстановка:
 ;
;
 ;
;  ;
; ;
;
 ;
;
Проинтегрируем
рациональную дробь:  ,
разложив ее на простейшие:
,
разложив ее на простейшие: .
.
Найдя
коэффициенты разложения, получим: А= ,
B=
,
B= ,
C=
,
C= .
.
Подставим их в разложение и проинтегрируем дроби:
 =
= ,
,
где
 =
= .
.
