IV. Функциональные ряды

Пусть последовательность функций, определенных на некотором множествеХ.

Определение. Ряд вида

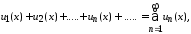(39)

членами которого являются функции 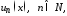называется функциональным.

Каждому значению 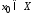соответствует числовой ряд 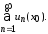Он может быть как сходящимся, так и расходящимся. Если ряд сходится, точка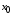называется точкой сходимости функционального ряда (39).

Множество 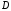всех точек сходимости функционального ряда называется егообластью сходимости. Сходимость функционального ряда в каждой точке называется поточечной сходимостью.

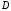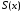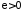Определение. Функциональный ряд (39) называется равномерно сходящимся в области к функции, если для любогосуществует номер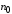, не зависящий от, такой, что

где n-я частичная сумма ряда, 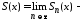сумма ряда.

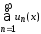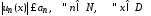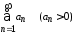Теорема (признак Вейерштрасса). Если члены ряда удовлетворяют неравенствами ряд сходится, то функциональный ряд сходится равномерно в области .

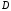
Числовой ряд , члены которого удовлетворяют неравенствам теоремы, называетсямажорантой (мажорантным рядом) для функционального ряда 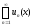, а сам функциональный ряд называется в этом случаемажорируемым на множестве .Из признака Вейерштрасса следует, что условие мажорируемости ряда является достаточным для его равномерной сходимости.

Сформулируем свойства равномерно сходящихся рядов:

1. (О непрерывности суммы функционального ряда)

Если на множестве функциональный ряд (39) с непрерывными членами сходится равномерно, то его сумманепрерывна на

.

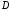2. (О почленном интегрировании)

Если функциональный ряд (39) с непрерывными членами сходится к функции 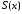равномерно на отрезке, то его можно почленно интегрировать на любом отрезке, и справедливо неравенство:

причем ряд сходится равномерно на отрезке .

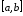3. (О почленном дифференцировании)

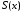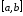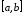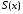Если функциональный ряд (39) с непрерывно дифференцируемыми на отрезке членами сходится к функции, а рядсходится равномерно на, то ряд (39) сходится равномерно на, его сумманепрерывно дифференцируемая функция, и справедливо неравенство:

.

V. Степенные ряды

Определение. Степенным рядом по степеням 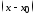называется ряд вида:

(40)

где 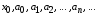действительные числа,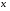принадлежит некоторому интервалу.

Числа 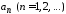называются коэффициентами степенного ряда.

Если то получим ряд по степенямх.

(41)

1. Теорема Абеля

Если степенной ряд сходится в точке, то он сходится абсолютно в интервалеи сходится равномерно на отрезке, где

Следствие. Если в точке степенной рядрасходится, то он расходится во всех точках, т. к.

Таким образом, всегда существует число R > 0, при котором степенной ряд сходится абсолютно для всех и расходятся для всех. В точкахряд может как сходиться, так и расходиться.

Число называется радиусом сходимости, а интервалинтервалом сходимости степенного ряда.

Для нахождения интервала сходимости степенного ряда используют достаточные признаки сходимости Даламбера и Коши (см. разделы II, V). Радиус сходимости можно найти по одной из следующих формул:

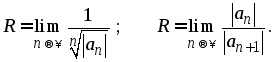
Пример 23. Найти интервал и радиус сходимости степенного ряда:

а) 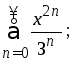b)

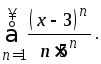
Решение.

а)

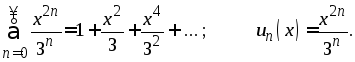
Для нахождения интервала сходимости воспользуемся признаком Коши и вычислим предел

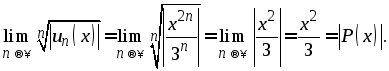
Ряд сходится, если , т.е.

Решая полученное равенство, найдем интервал сходимости ряда:

В точках получаем расходящийся ряд

Таким образом, область сходимости степенного ряда интервал , радиус сходимости

b)

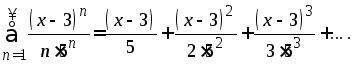
Найдем радиус сходимости данного ряда, для этого воспользуемся формулой

Тогда

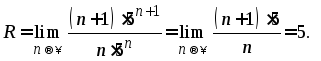
Интервал сходимости ряда найдем, решив равенство:

В точке имеем условно сходящийся ряд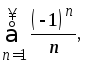а в точкерасходящийся гармонический ряд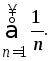Таким образом, областьсходимости данного ряда есть полуинтервал , радиус сходимости.

Замечание. Из теоремы Абеля и свойств равномерной сходимости рядов следует, что на интервале сходимости степенной ряд можно рассматривать как обыкновенный многочлен.

2. Ряды Тейлора и Маклорена

Рассмотрим некоторую функцию , определенную на интервале, и пусть. Допустим также, что функцияимеет в окрестности точкипроизводные любого порядка. Поставим функциив соответствие степенной ряд, (окрестностью точкиназывается любой интервал, содержащий эту точку ),

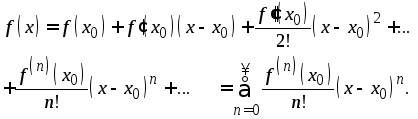(42)

0! = 1, n! = 1234 n, n N .

Такой ряд называется рядом Тейлора функции в точке.

Если , то ряд Тейлор имеет вид:

(43)

и называется рядом Маклорена.

Радиус сходимости ряда Тейлора может быть равен нулю или отличен от нуля. Причем, в последнем случае сумма ряда Тейлора может не совпадать с функцией. Если ряд Тейлора сходится к функции, для которой он составлен, то говорят, чторазложима в ряд Тейлора в окрестности точки.

Заметим, что частичные суммы ряда Тейлора

представляют собой многочлены Тейлора функции в точке. Если ряд сходится к функции, справедливо равенство

где 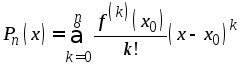многочлен Тейлора, остаточный член формулы Тейлора.

Напомним, что остаточный член формулы Тейлора может быть записан в одном из следующих видов:

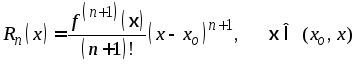форма Лагранжа,

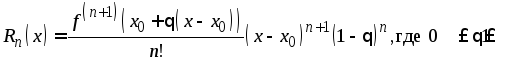форма Коши.

Имеет место необходимый и достаточный признак разложимости функции в ряд Тейлора.

Теорема 1. Для того, чтобы существовало разложение в ряд Тейлора бесконечно дифференцируемой в окрестности точки функциинеобходимо и достаточно, чтобы

где остаточный член формулы Тейлора,

Теорема 2. (Достаточный признак разложимости функции в ряд Тейлора). Если для все производные функции , ограничены одной и той же константойМ, то ряд Тейлора сходится к функции в интервале

Теорема 3. Если степенной ряд по степеням сходится к функциив окрестности точки, то он является рядом Тейлора функциив окрестности этой точки.

Приведем примеры разложения в ряд Маклорена основных элементарных функций: