
tmm
.pdf2.2. Планы положений звеньев групп и построение траекторий, описываемых точками звеньев механизма
Задачи о положениях, скоростях и ускорениях решаются применительно к группам Ассура, которыми образован механизм.
Эти задачи решаются в такой последовательности.
1.Выполняется структурный анализ и классификация механизма по Ассуру–Артоболевскому.
2.Указываются ведущие звенья (их количество соответствует степени подвижности механизма). Задаются их законы движения. При построении планов положений обычно задаются равномерным движением ведущего звена (ведущих звеньев). Выбирается обобщенная координата.
3.Выбирается масштаб построения чертежа.
4.Наносятся все неподвижные элементы кинематических пар механизма в некоторой координатной сетке в соответствии с их расположением.
5.По заданной обобщенной координате строится положение ведущего звена.
6.Последовательно по группам Ассура строится план положений механизма.
Масштабы построения выбираются таким образом, чтобы была возможность и достаточно точного построения, и наилучшим образом использовалось поле чертежа.
При вращательном движении ведущего звена в качестве обобщенной координаты используется угол, определяющий положение данного звена в выбранной системе координат (см. рисунки к задачам 60, 61…), при поступательном движении ведущего звена – соответствующая линейная координата. Само построение плана выполняется элементарными геометрическими построениями (рис. 2.2).
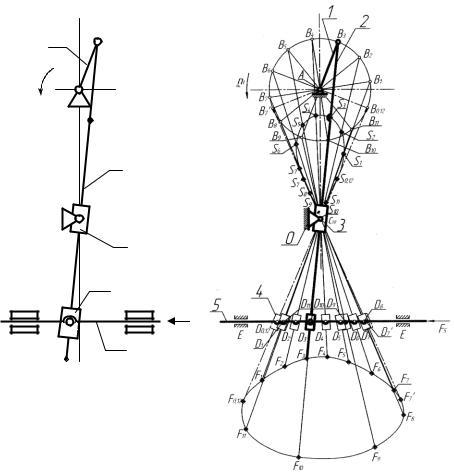
Для определения размера пространства, необходимого для работы механизма, траекторий, описываемых различными точками звеньев, выполняется, как правило, построение не менее 12 положений за цикл работы механизма. За начальное положения часто принимается одно из крайних положений, соответствующее началу рабочего хода. Последовательные положения интересующих точек соединяются кривой. Например, при ведущем кривошипе 1 (рис. 2.2) строится его 12 равноотстоящих положений – через 30º, нумерация начинается соответственно от крайнего левого положения по выходному звену 5, так как полезная сила, приложенная к звену 5, направлена влево.
41
1 |
|
B |
|
n1 |
|
|
|
A |
|
|
|
|
S |
|
|
|
|
2 |
|
а) |
C |
|
б) |
|
3 |
||
|
|
|
|
E |
4 |
|
E F5 |
D |
|
||
F |
|
5 |
|
|
|
|
Рис. 2.2. Схема механизма (а), план положений механизма и траектории характерных точек (б)
Рассмотрим пример, поясняющий порядок построения планов скоростей и ускорений, а также форму записей в поясняющей текстовой части.
На рис. 2.3,а приведена схема шестизвенного рычажного механизма с качающейся кулисой. Размеры звеньев и частота вращения ведущего звена – известны:
lAB =150 мм, lBC = 700 мм, lCD = 600 мм, lCF = 270 мм, lKL = 650 мм, n1 = 225 об/мин.
Этот механизм состоит из начального механизма – кривошипа 1 с вращательной кинематической парой В0,1 и двух последовательно присоединенных групп Ассура, содержащих звенья 2–3 и 4 –5. В общем виде формулу строения механизма можно записать в такой форме:
1– [2–3] – [4–5],
или в развернутом виде
B0,1– [B1,2–B2,3–B3,0] – [B2,4–П4,5–B5,0].
Это механизм 2-го класса.
42
а) |
|
б) |
|
|
|
в) |
|
г) |
|
|
|
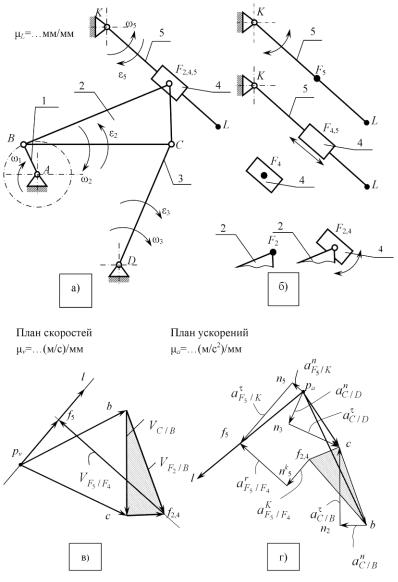
Рис. 2.3. К кинематическому исследованию методом планов:
а – схема механизма; б – фрагменты; в – план скоростей; г– план ускорений
Для лучшего понимания характера абсолютного и относительного движения звеньев кулисной пары и правильного составления векторных уравнений при построении планов скоростей и ускорений рядом показаны (см. рис. 2.3,б): отдельно звено 2 с точкой F2, звено 4 – камень кулисы с точкой F4 и звено 5 – кулиса с точкой F5 (на механизме эти точки совпадают).
Отдельно показаны соединения: звенья 2 и 4 образуют вращательную кинематическую пару В2,4, следовательно, относительное движение этих звеньев может быть только вращательным, а звенья 4 и 5 входят в поступательную кинематическую пару П4,5, и относительное движение этих звеньев – поступательное.
43

2.3. Построение планов скоростей механизма
Кинематический анализ выполняется последовательно от начального механизма (ведущего звена, для которого известен закон движения) по группам Ассура, начиная с первой присоединенной группы.
Для механизма, образованного только диадными группами (группами Ассура 2-го класса), на каждом этапе исследования присоединенной группы ищется такая точка механизма, движение которой может быть рассмотрено через две другие известные точки механизма согласно теореме о скоростях точек твердого тела.
Порядок выполнения кинематического анализа методом планов может быть структурирован следующим образом:
1.Вычерчивается механизм в масштабе в заданном положении.
2.Определяется скорость точки начального механизма, в которой присоединена первая группа Ассура, т. е. точки звена, закон движения которого задан. В данном случае это точка В звена 1:
|
|
VB =ω1 LAB , |
где |
|
|
ω = π n |
= 3,14 225 = 23,56 1 c . |
|
1 |
30 |
30 |
|
||
Подставив значения, получим
VB = 23,56 0,15 = 3,53 м/с.
3. Примем масштаб построения плана скоростей, например:
μv = 0,05 мммс. (Масштаб определяется абсолютными значениями вели-
чин скорости, располагаемым форматом, и его следует выбирать из ряда предпочтительных значений: 1; 2; 2,5; 4; 5; 10 и т. д. или 0,1; 0,2 и т. д.)
Вектор скорости точки В на плане отобразится отрезком длиной
V = VB = 3,53 = 70,6 мм, μv 0,05
он перпендикулярен кривошипу АВ и направлен в сторону вращения. (В дальнейшем будем записывать символом VB AB ). Концы векторов удобно обозначать теми же, но малыми буквами, что и на механизме.
Выбираем произвольную точку – полюс плана скоростей pv (см. рис. 2.3, в) и откладываем отрезок pv b=70,6 мм.
4. Ищется на механизме ближайшая точка, скорость которой может быть определена через две другие известные точки. В рассматриваемом примере такой точкой является точка С – центр кинематической пары между звеньями 2 и 3. Точка С принадлежит звеньям 2 и 3 (см.
44
рис. 2.3, а). Рассматривая звено 2 (твердое тело, для которого закон движения точки В уже определен), можно записать уравнение
VC =VB +VC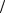 B .
B .
В силу предположения об абсолютной жесткости звеньев расстояние между точками В и С неизменно, следовательно, в своем относительном движении точка С относительно точки В может совершать только вращение, значит, вектор относительной скорости
VC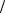 B CB.
B CB.
С другой стороны, рассматривая звено 3, совершенно аналогично можно записать: VC =VD +VC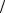 D . Здесь VD = 0 , а VC CD.
D . Здесь VD = 0 , а VC CD.
Таким образом, скомпонована система векторных уравнений
|
|
|
|
|
|
|
|
|
|
|
|
V |
|
=V |
B |
+V |
|||||||
|
C |
|
|
|
|
C B |
|||||
|
|
|
|
|
|
|
|
|
, |
||
V |
=V |
D |
+V |
||||||||
|
C |
|
|
|
|
C D |
|||||
в которой первые составляющие известны полностью по величине и направлению, а последние компоненты известны по их линиям действия. Данная система может быть решена графически.
Заметим, что суть метода планов (скоростей, ускорений, …) заключается в графическом решении системы векторных уравнений или закольцованного уравнения.
Из точки b плана проводим прямую, перпендикулярную ВС, а из полюса (поскольку скорость точки D равна 0) – перпендикуляр к CD и на пересечении получаем точку с, это единственная точка, удовлетворяющая одновременно обоим уравнениям системы. Отрезок bc представляет относительную скорость точки С относительно В. Направление этой скорости (согласно уравнению) от b к c. В силу характера геометрических построений длины полученных на плане отрезков в том же самом масштабе представляют искомые относительные скорости. Измеряя их на плане и переводя через масштабный фактор, получим
VC = pvc μv = 68 0,05 = 3,4 м/с; VC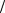 B = cb μv = 64 0,05 = 3,2 м/с.
B = cb μv = 64 0,05 = 3,2 м/с.
5. Скорость точки F2. Скорость точки F2 проще определить на основании свойства подобия: bf2 c на плане скоростей должен быть подобен BF2 C с сохранением того же порядка обхода букв (на плане скоростей образуются фигуры, подобные и сходственно расположенные жестким звеньям механизма, но повернутые на 90° в сторону мгновенного вращения). Построив на стороне bc треугольник, подобный треугольнику на механизме с сохранением того же порядка обхода букв,
45

получим точку f2. Соединив точку f2 c полюсом, получим вектор скорости точки F2.
6. Скорость точки F4. Так как звенья 4 и 2 образуют вращательную кинематическую пару,
VF 4 =VF 2 =4,6 м/с.
Точка F4 является точкой присоединения к механизму следующей группы Ассура, образованной звеньями 4 и 5. Для последней группы Ассура теперь известны скорости двух точек звеньев 4 и 5 (F4 и K). Скорость точки K равна 0. Теперь можно определить скорость в точке внутренней для данной группы кинематической пары.
7. Скорость точки F5. Рассматривая соединения звеньев 4 и 5, получим уравнение
VF 5 =VF 4 +VF 5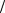 F 4.
F 4.
Здесь VF 5 F 4 // KL (относительное движение – поступательное).
Рассматривая точку F5 как принадлежащую звену 5, следует VF 5 KL и можно записать VF 5 =VK +VF 5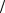 K .
K .
Таким образом, опять скомпонована система двух векторных уравнений:
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
V |
|
=V |
K |
+V |
F 5 K |
|
|||||||||
|
F 5 |
|
|
|
|
|
|
, |
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
=V |
|
|
|
+V |
|
|
|||||||
V |
F 4 |
F 5 F 4 |
|
||||||||||||
|
F 5 |
|
|
|
|
|
|
|
|
||||||
которая решается графически, дополняя план скоростей: из конца вектора f2,4 проводим линию, параллельную KL, а через полюс проводим линию, перпендикулярную KL. На пересечении этих направлений получим точку f5.
8. Скорость точки L. Скорость точки L найдем на основании свойства подобия из пропорциональных отрезков
|
|
|
|
|
kl |
= |
KL |
, |
|
|||
|
|
|
|
|
kf |
|
|
|
|
|
||
|
|
|
|
|
5 |
|
KF |
|
||||
отсюда |
|
|
|
|
|
5 |
|
|
||||
|
|
|
KL |
|
|
|
|
65 |
|
|||
|
kl = kf5 |
|
|
= 30 |
= 49 мм. |
|||||||
|
KF |
|
|
|
||||||||
|
|
|
|
|
|
40 |
|
|||||
Из плана получим |
|
|
5 |
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
||
VF 5 = pv f5 μv = 30 0,05 =1,5 м с, |
||||||||||||
VF |
F |
4 |
= f5 f4 μv = 86 0,05 = 4,3 м с, |
|||||||||
5 |
|
|
|
|
|
|
|
|
|
|
|
|
VL = pvl μv = 49 0,05 = 2,45 м с.
9. Определение угловых скоростей звеньев. Угловые скорости звеньев определятся из отношений:
46
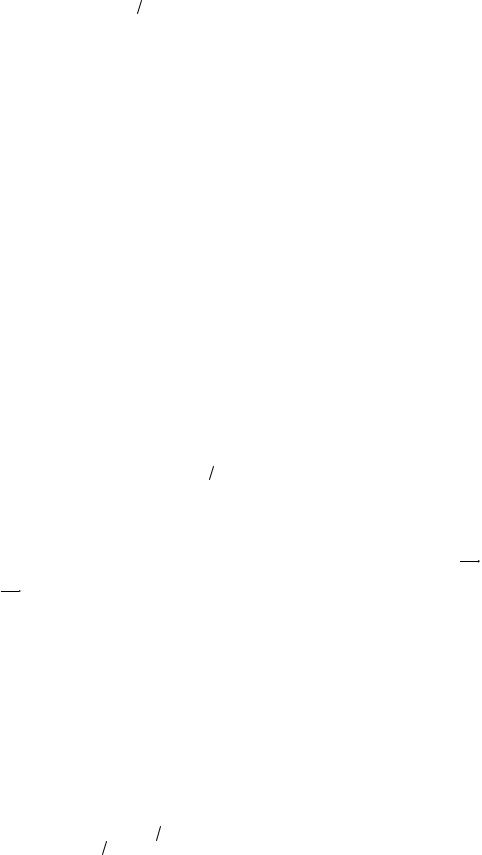
ω2 |
= |
VC B |
|
= |
3,2 |
= 4,56 1/c, |
|
||||||||||
lCB |
0,7 |
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
V |
|
|
VF |
|
3,4 |
|
|
|||||||
ω = |
C |
= |
|
|
5 |
|
|
= |
|
|
|
= 5,66 |
1/c, |
||||
|
|
|
|
|
|
|
|
||||||||||
3 |
|
lCD |
|
|
lF K |
|
0,6 |
|
|
||||||||
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
5 |
|
|
|
|
|
|
|
|
ω |
|
=ω = |
|
VF |
= |
1,5 |
|
= 3,75 |
1/c. |
||||||||
4 |
|
|
|
5 |
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|||||||||
|
|
5 |
|
|
|
lF K |
|
0,4 |
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
5 |
|
|
|
|
|
|
|
|
Направления мгновенных угловых скоростей ω2, ω3, ω4,5 определяются направлениями линейных скоростей точки С относительно В, точки С относительно D и точки F5 относительно K соответственно (на рис. 2.3,а показаны эти направления). Для определения направлений угловых скоростей звеньев векторы относительных скоростей с плана переносим в соответствующие точки механизма, например, bc (VC/B ) переносим в точку С, и направление вращения звена ВС – по часовой стрелке.
2.4. Построение планов ускорений механизма
Построение плана ускорений ведут в том же порядке и последовательности, как и план скоростей.
1. Ускорение точки В звена 1. Так как ω1=const, угловое ускорение ε1=0 и тангенциальное ускорение aτB A = 0 . Следовательно, полное уско-
рение точки В будет равно нормальному ускорению, т. е. aB = aBn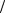 A =ω12 l AB = 23,56 0,15 =83,2 м
A =ω12 l AB = 23,56 0,15 =83,2 м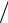 с2 .
с2 .
Нормальное ускорение всегда направлено к центру вращения, в данном случае от В к точке А (будем в дальнейшем обозначать BA ),
т. е. aBn A // BA.
A // BA.
2. Ускорение точки С.
Рассматривая звено 2, можно записать уравнение
aC = aB + aC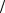 B = aB + aCn
B = aB + aCn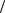 B + aCτ
B + aCτ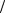 B .
B .
Здесь аВ – переносное ускорение; аС/ В – относительное ускорение. Точка С относительно В совершает вращательное движение.
Нормальную составляющую ускорения можно найти, поскольку угловая скорость звена ВС известна:
aCn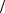 B =ω22 lCB = 4,562 0,7 =14,62 м
B =ω22 lCB = 4,562 0,7 =14,62 м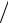 с2 ,
с2 ,
|
|
|
an |
14,62 |
|
|
a n |
|
= |
C B |
= |
=14,62 мм; |
|
|
|
1 |
||||
C |
B |
|
μa |
|
||
47

aCn B // CB
(вектор параллелен СВ и направлен от С к В).
Для тангенциального ускорения aCτ B CB известна линия дейст-
вия.
Рассматривая движение звена 3, можно записать
aC = aD + aC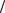 D = aD + aCn
D = aD + aCn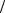 D + aCτ
D + aCτ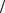 D .
D .
Здесь переносное ускорение аD =0 (точка D – неподвижна):
an |
=ω2 |
l |
= 5,662 0,6 =19,26 мм, |
|||
C D |
|
3 |
CD |
|
|
|
|
|
an |
|
|
19,26 |
|
a n |
= |
C D |
= |
=19,26 мм, |
||
|
1 |
|||||
C D |
|
μa |
|
|||
a n |
// CD , |
aτ |
CD. |
|||
C D |
|
|
|
|
C D |
|
В результате для определения ускорения точки С имеется система векторных уравнений
a |
= a |
B |
+ a |
= a |
B |
+ a n |
+ aτ |
|
, |
|
|||
|
C |
|
C B |
|
C B |
|
C B |
|
|
||||
|
|
= a |
|
+ a |
= a |
|
+ a n |
|
+ a |
τ |
|
. |
|
a |
D |
D |
|
|
|||||||||
|
C |
|
C D |
|
|
C D |
C D |
|
|||||
В данной системе тангенциальные ускорения известны по линиям действия, все остальные векторы известны полностью. Данная система может быть решена графически.
3. Если принять масштаб плана ускорений μa =1 |
м с2 |
, вектор ус- |
|||
мм |
|||||
корения В определится отрезком |
|
|
|
||
|
|
|
|
||
aB = aB = |
83,2 |
=83,2 мм. |
|
|
|
μa |
1 |
|
|
|
|
На плане (см. рис. 2.3,г) – это отрезок pa b, где pa – полюс плана ускорений.
Из конца вектора pa b откладывается отрезок bn2 в соответствии с величиной и направлением aCn B и из конца его проводится направление
(линия действия) тангенциального ускорения aCτ B .
Из полюса откладывается вектор отрезок pan3 в соответствии с величиной и направлением нормального ускорения aCn D , из конца его
проводится линия действия тангенциального ускорения aCτ D . На пересечении этих линий векторов aCτ B и aCτ D получается точка с. Соединив
48

её с полюсом, получим вектор полного ускорения точки С, а отрезок bc на плане представит относительное ускорение aC B.
Из плана могут быть найдены:
aC = pac μa = 40 1 = 40 м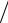 с2 , aC
с2 , aC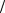 B = cb μa = 43 1 = 43 м
B = cb μa = 43 1 = 43 м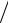 с2 , aτC
с2 , aτC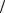 B = aCτ
B = aCτ B μa = 40 1 = 40 м
B μa = 40 1 = 40 м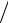 с2 , aτC
с2 , aτC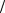 D = aCτ
D = aCτ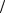 D μa = 34 1 = 34 м
D μa = 34 1 = 34 м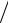 с2 .
с2 .
4. Ускорение точки F2. Ускорение точки F2, как и скорость, может быть найдено на основании свойства подобия. На стороне bc плана ускорений построится фигура (в данном случае – треугольник), подобная звену 2 на механизме, т. е. bf2 c BF2 C с тем же правилом обхода. Соединяя точку f2 с полюсом, получим вектор pаf2 полного ускорения
точки F2.
Из плана ускорений будет определена величина:
aF2 = pa f2 μa = 41 1 = 41 м с2 .
с2 .
Все характерные точки группы 2–3 исследованы. Можно перейти к анализу следующей присоединенной группы Ассура – группы 4–5.
5. Ускорение точки F4. Звенья 2 и 4 образуют вращательную кинематическую пару, следовательно, линейные ускорения этих точек F4 и
F2 будут равны, т. е.
aF4 = aF2 = 41 м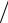 с2 .
с2 .
6. Ускорение точки K внешней кинематической пары известно.
aK=0.
7. Ускорение точки F5. Звенья 4 и 5 образуют поступательную кинематическую пару. Звено 5 (кулиса) является подвижной направляющей для звена 4 (камня), тогда
|
|
|
|
aF = aF |
+ aFK |
F |
+ aFr |
F , |
||||
|
|
|
|
|
5 |
|
4 |
|
5 |
4 |
5 |
4 |
VF |
F |
где кориолисово ускорение |
|
|||||||||
5 |
4 |
aK |
|
= 2 ω V |
|
|
= 2 3,75 4,3 = 32,2 м с2 . |
|||||
|
|
|
|
|
|
|
|
|
|
|
||
|
|
F |
F |
|
5 |
F |
F |
|
|
|
|
|
ω5 |
|
5 |
4 |
|
|
|
5 |
4 |
|
|
|
|
|
|
Для определения направления этого ус- |
||||||||||
|
|
|
||||||||||
aFK |
|
корения нужно вектор относительной скоро- |
||||||||||
F |
сти |
VF5/F4 |
повернуть на |
90° в |
сторону ω5 |
|||||||
5 |
4 |
(на рис. 2.4 показан фрагмент к определению |
||||||||||
|
|
|||||||||||
Рис. 2.4. К определению |
направления кориолисова ускорения). |
|||||||||||
направления кориолисова |
|
Ускорение |
|
aF |
F |
– это относительное |
||||||
ускорения |
|
|
|
|
|
|
5 |
4 |
|
|
|
|
ускорение |
в |
|
поступательном |
движении |
||||||||
|
|
|
||||||||||
49

звеньев (его также называют релятивным), оно всегда направлено по
кулисе (векторы a K |
и a r |
|
всегда перпендикулярны между собой). |
||||||||||||||||||
С другой стороны, рассматривать движение точки F5 можно через |
|||||||||||||||||||||
твердое тело – звено 5. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
Ускорение точки F5 можно выразить уравнением |
|
||||||||||||||||||||
aF |
= aK |
+ aF K = aK |
+ aFn K |
+ aFτ |
K |
|
|||||||||||||||
|
|
5 |
|
|
|
|
|
|
|
|
5 |
|
|
|
|
|
5 |
|
5 |
|
|
(здесь aK = 0 , точка K неподвижна), |
|
|
|
|
|
|
|
||||||||||||||
an |
|
K |
=ω2 |
|
l |
F K |
= 3,752 0,4 = 5,61 м с2 , |
||||||||||||||
F |
|
|
|
|
5 |
|
|
|
|
|
|
|
|
|
|
|
|
||||
5 |
|
|
|
|
|
|
|
|
|
5 |
|
|
|
|
|
|
|
|
|
|
|
aFn |
|
|
= |
aFn |
|
K |
|
= |
5,61 |
= 5,6 мм, |
|
|
|
|
|||||||
|
K |
|
|
5 |
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
μa |
|
|
1 |
|
|
|
|
|
|
|||||||||
5 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
a n |
|
K |
// F |
5 |
K, |
|
aτ |
K |
F K. |
|
|
|
|
||||||||
F |
|
|
|
|
|
|
|
|
|
F |
|
|
5 |
|
|
|
|
||||
5 |
|
|
|
|
|
|
|
|
|
|
|
5 |
|
|
|
|
|
|
|
|
|
Таким образом, для исследования группы Ассура 4–5 определилась |
|||||||||||||||||||||
система векторных уравнений |
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
K |
|
|
|
|
|
r |
|
|
|
|
aF5 |
= aF4 + aF5 F4 + aF5 F4 , |
|
|
|
|
||||||||||||||||
|
|
|
= a |
|
|
|
+ a |
|
|
= a |
|
+ a n |
+ aτ |
. |
|||||||
a |
F5 |
K |
|
F5 |
K |
K |
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
F5 K |
|
F5 K |
|
||||||||
Из точки f4 (она же f2) проводится вектор aFK |
F |
в соответствии с его |
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
5 |
4 |
|
|
направлением. Из конца его проводится линия действия релятивного ускорения aFr5  F4 .
F4 .
Из полюса pa откладывается вектор aFn5 K , а из конца его проводится направление aFτ5 K . На пересечении aFτ5 K и aFr5 F4 будет получена
точка f5. Соединив её с полюсом, получим вектор полного ускорения точки F5. Из плана посредством измерения полученных отрезков и перевычисления через масштаб найдутся
aF5 = pa f5 μa = 61 1 = 61 м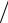 с2 ,
с2 ,
aFr |
F |
= aFr |
F |
μa = 37 1 = 37 м с2 , |
5 |
4 |
5 |
|
4 |
aτF |
K |
= aFτ |
K μa = 60 1 = 60 м с2 . |
|
5 |
|
5 |
|
|
7. Ускорение точки L. Ускорение точки L может быть найдено на основании свойства подобия из пропорциональности отрезков:
kl = KL , kf5 KF5
отсюда
50
