FNP

Добавил:

Upload Опубликованный материал нарушает ваши авторские права? Сообщите нам.

Вуз:

Томский Политехнический Университет

Предмет:

[НЕСОРТИРОВАННОЕ]

Файл:

Для функции z3(x, y) имеем предел по направлению :

(x, y) = lim

2t2(cos2 α)(t sin α)

t(cos2 α)(sin α)

t→+0 t4 cos4 α + t2 sin2 α

t→+0 t2 cos4 α + sin2 α

.pdf

Скачиваний:

Добавлен:

29.05.2015

Размер:

2.23 Mб

Скачать

☆

<<< < Предыдущая 1 2 34 / 194 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 > Следующая >>>

Глава 2. Предел и непрерывность функции нескольких переменных

Пример 4.4. Вычислить двойные пределы

y→→0

x + y

y→→0

x + y

y→→0

1) lim

sin xy

;

2) lim

1/x2

)

x2y2

;

3) lim(x

+ y

x 0

2 2

x 0

Решение. 1. Из очевидного неравенства

(x − y)2 0 (4.16)

следует

x2 + y2 2xy.

С уч¨етом неравенства | sin α| |α| имеем оценку

0 | sin xy| |xy| x2 + y2

и, следовательно,

0	\| sin xy\|						x2 + y2 .
						2
		x2 + y2				2
А поскольку, согласно примеру 4.1, при a = 1/2
	y→→0
	y→→0			x2 + y2 = 0,
	lim			x2 + y2 = 0,
	x 0
то в силу теоремы 4.1			sin xy
	lim		sin xy				= 0.


	y→→0		x + y
	x 0		2		2

2. Для второго предела воспользуемся неравенством (4.16) в виде

						xy						1		.
			2					2						.
			2			+ y		2			2
				x		+ y					2
Тогда						\|xy\|									1
		0				\|xy\|									1
		0								2
						2	+ y			2					2
						x	+ y								2
и, соответственно,							1/x2										1/x2
0			xy				1/x2								1		1/x2
0	x2 + y2														2		.

Поскольку					2											2
y→→0	2						x→0 2
lim	1		1/x			= lim					1				1/x		= 0,
x 0
то в силу теоремы 4.1										1/x2
y→→0 x						xy				1/x2
y→→0 x						+ y							= 0.
lim													= 0.
x		0			2				2

5. Предел функции в точке по множеству и по направлению								31
3. Для третьего предела воспользуемся неравенством (4.16) в виде
x2y2		(x2 + y2)2					.
x2y2							.
					4
Тогда в предположении 0 < x2 + y2 < 1 из неравенства
1 (x2 + y2)x2y2 (x2 + y2)(x2+y2)/4
и предела
lim(x2 + y2)(x2+y2)/4 = lim tt2/4 = lim e(t2/4) ln t = 1
x→0	t→+0						t→+0
y→0
следует, что					x2y2
2	+ y		2	)	x2y2	= 1.
lim(x	+ y			)		= 1.

x→0 y→0

5.Предел функции в точке по множеству и по направлению

Для функции одной переменной понятие предела функции в точке было дополнено понятием одностороннего предела: правостороннего и левостороннего. Понятие предела функции нескольких переменных дополним понятием предела функции в точке по множеству.

Число A называется пределом функции f(x) в точке x0 по множеству
X D(f) и обозначается											(5.1)
A = lim f(x),											(5.1)
x→x0
x X								˙
если для любого ε > 0 существует δ > 0 такое, что для всех					x			˙			∩ X
если для любого ε > 0 существует δ > 0 такое, что для всех					x			S(x0, δ)			∩ X
справедливо \|f(x) − A\| < ε, или
˙											(5.2)
ε > 0 δ > 0 x S(x0, δ) ∩ X \|f(x) − A\| < ε.											(5.2)
Если множество X представляет собой отрезок луча L:

x = x0 + t, t 0,				), (							= 1,
выходящего из точки x0 в направлении вектора = (		, ...,		), (	)		+...+(		)		= 1,
	1		n	1		2			n	2

то n-кратный предел (5.1) можно свести к однократному пределу по параметру

t → +0, называемому пределом по направлению.			1		n
Пределом функции f(x) в точке x0 по направлению = (				, ...,		), \| \| = 1,
называется выражение
						(5.3)
	lim f(x) = lim f(x0 + t),					(5.3)
	x→x0	t→+0
	˙
	x O(x0)∩L

где L — луч, выходящий из точки x0 в направлении вектора .				и осью Ox, т.е.
При n = 2 направление зада¨ется углом α между вектором				и осью Ox, т.е.

= (cos α, sin α) и, следовательно,
lim	f(x, y) =	lim f(x0 + t cos α, y0 + t sin α).				(5.4)
y→y0		→
x→x0		t +0
˙	,y0)∩L
(x,y) O(x0	,y0)∩L

Глава 2. Предел и непрерывность функции нескольких переменных

Пример 5.1. Вычислить предел функции

x2y√

u(x, y, z) =

(5.5)

−

+ y2 + z2 + 1

√

в точке x0 = y0 = z0 = 0 по направлению = (1/

, 1/

3).

Решение. Пусть L — луч, выходящий из точки x0 = y0 = z0 = 0 в направлении

определяется соотношением

вектора , тогда координаты точек луча L

x = x0 + 1t =

√

t, y = y0

+ 2t =

√

t, z = z0

+ 3t =

√

t, t > 0,

подстановка которых в (5.3) приводит к пределу по направлению луча L:

√

x y√z

(t /3)(t/ 3) t/ 3

lim

→

+ z

+ 1

= t +0

x + y

−

→

√t + 1

−

y→0

(x,y,z→)

t7/2(√

lim

t2 + 1

+ 1)

lim

t2 + 1

+ 1)

= 0.

4/4

t +0

√

+ 1 + 1)

7/4

t +0

→

(

t + 1

− 1)(

→

Пример 5.2. Вычислить предел функции

z(x, y) = (x2 + y2)a, a > 0,

в точке x0 = y0 = 0 по направлению

= (cos α, sin α).

Решение. Пусть L — луч, выходящий из точки x0		= y0 = 0 под углом α к оси
Ox. Тогда координаты его точек связаны соотношением
	x = t cos α, y = t sin α,

и, следовательно, согласно (5.4), предел по направлению вектора :
lim	(x2 + y2)a = lim (t2 cos2 α + t2 sin2 α)a = lim t2a = 0.
x→0	t→+0	t→+0
y→0

(x,y) L

Это означает, что значение предела не зависит от направления и совпадает со значением двойного предела

lim(x2 + y2)a = 0,

x→0 y→0

найденным в примере 4.1.

Пример 5.3. Вычислить пределы функций

z1 =

2xy

; z2

x2y2

; z3 =

2x2y

+ (x

− y)

x + y

x y

x + y

в точке по направлению . x0 = y0 = 0 = (cos α, sin α)

5. Предел функции в точке по множеству и по направлению

Решение. Координаты точек луча L, выходящего из точки x0 = y0 = 0 в направ-

лении вектора = (cos α, sin α), образующего с осью Ox угол α, определяются

соотношением

x = t cos α,

y = t sin α,

и, следовательно, согласно (5.4), имеем для z1(x, y) предел

lim

z1 = lim

(2t cos α)(t sin α)

= 2 sin α cos α = sin 2α,

(5.6)

x→0

t→+0 t2 cos2 α + t2 sin2 α

y→0

(x,y) L

значение которого зависит от направления, т.е. от угла α.

Для функции z2(x, y) имеем предел по направлению :

lim

z2 = lim

(t2 cos2

α)(t2 sin2 α)

α) + t2(cos α

sin α)2

x→0

t→+0 (t2 cos2 α)(t2 sin2

−

y→0

(x,y) L

который при α = π/4 и α = 5π/4 равен

lim

t4(cos2 α)(sin2 α)

= lim

t4(cos2 α)(sin2 α)

= 0,

t→+0 t4 cos2 α sin2 α + t2(cos α − sin α)2

t→+0 t2(cos α − sin α)2

а при α = π/4 и α = 5π/4, т.е. при cos α = sin α = ±1/√

, равен

lim

= 1.

Таким образом,

t→+0 t4/4 ± t2(1/√2 − 1/√2)

α = 4 , α =

54 ,

т.е. y = x; .

lim

z2 = lim z2(t cos α, t sin α) = 0,

y→0

t→+0

α =

т.е. y = x

, α =

→

5π

x 0

(x,y) L

Это означает, что пределы по всем направлениям, за исключением прямой y = x, равны между собой и равны нулю. Пределы по направлениям с углами α = π/4 и α = 5π/4, т.е. на прямой y = x, в отличие от других равны единице.

(x,y) L

который при α = 0 равен

2 lim = 0,

t→+0 t2 cos4 α

а при α = 0 имеет то же значение:

2 lim	t(cos2	α)(sin α)		t(cos2 α)(sin α)
			= 2 lim			= 0,
				sin2
t→+0 t2 cos4 α + sin2 α			t→+0		α

34 Глава 2. Предел и непрерывность функции нескольких переменных

т.е.
lim	z3	(x, y) = lim z3(t cos α, t sin α) = 0
x→0		t→+0

y→0 (x,y) L

для всех направлений.

Таким образом, предел первой функции z1(x, y) меняется в зависимости от направления как sin 2α; пределы функции z2(x, y) по всем направлениям, за исключением одного, равны между собой и равны нулю. Исключением является прямая y = x, при стремлении по которой предел функции z2(x, y) равен единице. Наконец, для функции z3(x, y) пределы по всем направлениям без исключения равны между собой и равны нулю.

Возвращаясь к пределу функции в точке x0 по множеству M, отметим, что из существования предела

lim f(x)

x→x0x M

следует существование предела

lim f(x)

x→x0x M

для любого подмножества M M, для которого точка x0 является предельной. В частности, из существования двойного предела функции f(x, y) при (x, y) → (x0, y0) следует существование предела функции f(x, y) в точке (x0, y0) по любому направлению и равенство этих пределов двойному пределу функции f(x, y) при (x, y) → (x0, y0), что и иллюстрируют результаты примеров 4.1 и 5.2.

Обратное утверждение неверно. Из результатов примеров 4.4 и 5.3 следует, что из существования и равенства пределов по любому направлению в точке (x0 = 0, y0 = 0) для функции z3(x, y) не вытекает существование в этой точке е¨ двойного предела. Следующий пример поясняет этот результат.

Пример 5.4. В примере 5.3 было показано, что пределы функции

2x2y z3(x, y) = x4 + y2

в точке x0 = 0, y0 = 0 по всем направлениям равны между собой и равны нулю. В примере же 4.4 было показано, что двойной предел этой функции в той же самой точке не существует. Указать множество, по которому предел функции z3(x, y) в точке x0 = 0, y0 = 0 отличен от нуля.

Решение. Рассмотрим параболу L: y = px2, p = 0, проходящую через точку x0 = y0 = 0. Поскольку значение функции z3(x, y) на параболе L постоянно:

	2x2y			2x2px2		=	2p	,
z3(x, y) x,y L = x4		+ y2	y=px2 = x4		+ p2x4	=	1 + p2	,

то предел функции z3(x, y) при стремлении к точке x0 = y0 = 0 по параболе L равен этому значению:

lim	2x2y		lim	2p		2p	.
lim	x4 + y2	=	lim	1 + p2	=	1 + p2 = 0	.
x→0	x4 + y2	=	x→0	1 + p2	=	1 + p2 = 0
y→0			y→0
(x,y) L			(x,y) L

5. Предел функции в точке по множеству и по направлению

Таким образом, парабола L представляет собой множество, предел по которому в точке x0 = y0 = 0 отличается от предела по любому направлению. Это означает, что пределы по двум пересекающимся множествам: параболе L: y = px2 и прямой L: y = kx, имеют различные значения. Этим и объясняется, что двойной предел функции z3(x, y) в точке x0 = y0 = 0 не существует. Этот же результат был получен в примере 4.4 с помощью определения двойного предела функции по Гейне.

Пример 5.5. Вычислить двойной предел
lim	x − y	.	(5.7)
x→0 x + y
y→0

Решение. Пусть L — прямая y = kx, тогда предел в этой точке по этой прямой равен

lim	x − y	=	lim	x − kx	lim	1 − k	=	1 − k	.
x→0	x + y		x→0	x + kx x→0		1 + k		1 + k
y→0			y→0		y→0
(x,y) L			(x,y) L		(x,y) L

Этот предел зависит от углового коэффициента прямой k; следовательно, двойной предел (5.7) не существует.

Пример 5.6. Для пределов
1) lim			ex/(x2+y2);	2) lim ex2−y2		sin 2xy
x	→	0		x→∞
				y	→∞
y→0			L
(x,y)				(x,y) L

указать направления луча
			L: = (cos α, sin α), по которым существуют конечные

пределы.

Решение. Согласно определению (5.4),

lim

x→0 y→0

(x,y) L

2	2	) = lim et cos α/(t	2		2	2	2	lim (cos α/t)	.
ex/(x	+y	) = lim et cos α/(t		cos		α+t	sin	α) = lim ecos α/t = et→+0	.
		t→+0						t→+0

Этот предел будет иметь конечное значение при условии cos α 0, т.е. если π/2 α 3π/2, поскольку

lim cos α = 0

при α1

= 2 , α2 =

32 ;

t→+0 t

при π < α < 3π .

−∞

В силу этого

при α1

, α2 =

3π

;

lim (cos α/t)

lim ex/(x2+y2) = et→+0

3π

при

→0

< α < .

→

(x,y) L

36 Глава 2. Предел и непрерывность функции нескольких переменных

Для второй функции предельной точкой является бесконечно удал¨енная точ-

					вычисляется заменой
ка. В этом случае предел по направлению = (cos α, sin α)					вычисляется заменой
x = t cos α, y = t sin α при t → +∞:
lim ex2−y2	sin 2xy =	lim et2(cos2 α−sin2 α) sin(2t2 cos α sin α) =
x→∞	t	→	+	∞
y→∞		→		∞
(x,y) L					et2 cos 2α sin(t2 sin 2α).
				= lim	et2 cos 2α sin(t2 sin 2α).
				t→+∞
Поскольку t2	→ +∞, а sin(t2 sin 2α) — ограниченная функция, то предел будет

конечным при условии cos 2α 0 или sin 2α = 0. Однако, если учесть, что при cos 2α = 0, sin 2α = 1, предел

lim e0 sin(t2)

t→+∞

не существует, то остается только условие cos 2α < 0, т.е. π/4 < α < 3π/4 и 5π/4 < α < 7π/4, и условие sin 2α = 0, т.е. α = 0 или α = π, при которых

lim ex2−y2 sin 2xy =	lim et2 cos 2α sin(t2 sin 2α) = 0.
x→0	t→+∞
y→0
(x,y) L

Пример 5.7. Вычислить двойные пределы

1) lim(1 + xy)2/(x2+xy);

x→0 y→2

2) lim (x2 + y2)e−(x+y).

x→∞ y→∞

Решение. Провед¨ем тождественные преобразования:

(1 + xy)2/(x2+xy) = [(1 + xy)1/xy]2y/(x+y)

и обозначим t = xy. Тогда если x → 0, y → 2, то t → 0 и

lim(1 + xy)1/xy = lim(1 + t)1/t = e.

x→0	t→0
y→2

Учитывая, что				2y
			lim	2y		= 2,
			lim			= 2,
			x→0 x + y
получим			y→2
получим					2/(x2
			lim(1 + xy)		2/(x2	+xy)	2
			lim(1 + xy)				= e .
			x→0
			y→2

2. Рассмотрим предел по направлению = (cos α, sin α) в бесконечно удал¨енной
точке:
lim (x2	+ y2)e−(x+y) =	lim (t2 cos2 α + t2 sin2 α)e−t(cos α+sin α) =						lim t2e−t(cos α+sin α).
x→∞		t +	∞				t	+	∞
y→∞		→	∞					→	∞

(x,y) L

6. Повторные пределы

Если α ]0, π/2[, то cos α + sin α = 0, поэтому, учитывая, что показательная функция растет быстрее степенной, получим

lim t2e−t(cos α+sin α) = 0. t→+∞

Если x = −y, т.е. α = 3π/4, то cos α + sin α = 0 и

lim t2 = +∞.

t→+∞

Таким образом, при разных α получим разные предельные значения, и, значит, исходный двойной предел не существует.

Пример 5.8. Вычислить

y→→∞a	1		x2	/(x+y)
y→→∞a	1 +	x
1) lim	1 +			;
x

2) lim

x→1 y→0

ln(x + ey)

. x2 + y2

Решение. 1. В силу непрерывности показательной и степенной функций имеем

lim

x→∞ y→a

1 x2/(x+y)

1 + x

y→→∞a	1 + y/x			x
	1		1		x
= lim exp		ln	1 +		= e.
x

2. Пользуясь непрерывностью логарифмической функции и тем, что


	y→→0
	y→→0		x2 + y2 = 1,
	lim		x2 + y2 = 1,
	x 1
получим	ln(x + ey)					ln 2
lim	ln(x + ey)				=	ln 2	= ln 2.
lim					=		= ln 2.
y→→0	x	+ y				1
x 1	2			2

6.Повторные пределы

Выше мы определили n-кратный предел функции f(x):

lim f(x)

x→x0

по совокупности переменных при одновременном стремлении всех аргументов к их пределам. Кроме того, был определ¨ен предел по множеству X:

lim f(x),						(6.1)
x→x0
x X
		1	, ...,	n	)	(по лучу L), представляю-
и, в частности, предел по направлению = (			, ...,		)	(по лучу L), представляю-
щий собой однократный предел по параметру t (5.4):
lim f(x) =
lim f(x) =	lim f(x0 + t).
x→x0	t→+0

x L

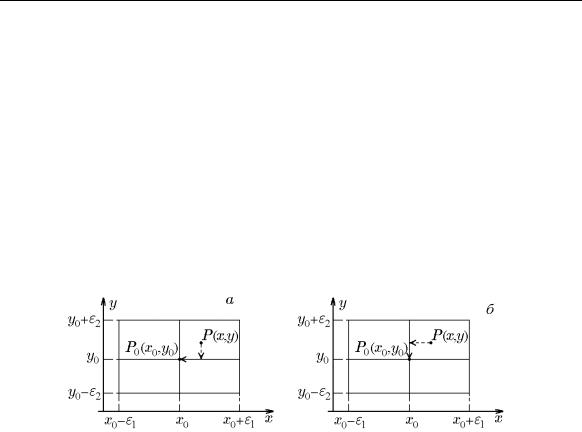
38	Глава 2. Предел и непрерывность функции нескольких переменных

Если в качестве множества X в (6.1) выбрать ломаную, соединяющую точкиx и x0, звенья которой параллельны координатным осям, мы получим последовательность предельных переходов по каждой переменной в отдельности в том или ином порядке. Такие пределы называются повторными. Сначала рассмотрим повторные пределы для функции двух переменных.

				˙
Если функция f(x, y) определена на множестве Π(x, y, ε1, ε2) = {(x, y)\|0 <
\|x − x0\| < ε1, 0 < \|y − y0\| < ε2}, а функция
	g(x) = lim f(x, y)			(6.2)
	y→y0
определена в ρ˙(x0, ε1) = (0 < \|x − x0\| < ε1), то предел
x→x0	x→x0	y→y0		(6.3)
lim	g(x) = lim	lim	f(x, y)

называется повторным, а предел (6.2) — его внутренним пределом (рис. 11,a).

Рис. 11.

Аналогично определяется повторный предел (рис. 11,б)

y→y0	x→x0		(6.4)
lim	lim	f(x, y) .

Существование повторных пределов (6.3), (6.4) определяется условиями существования двух пределов по отрезкам ломаной, параллельным координатным осям, в порядке, показанном на рис. 11,a и 11,б, соответственно.

Пример 6.1. Найти повторные пределы для функций

z1(x, y) =

2xy

; z2

(x, y) =

x2y2

; z3(x, y) =

2x2y

+ (x

− y)

x + y

x y

x + y

в точке x0 = y0 = 0.

Решение. Все повторные пределы этих функций равны нулю, поскольку внутренние пределы равны

	lim z1(x, y) = lim z2(x, y) = lim z3(x, y) = 0,
	y→0	y→0	y→0
(x=0)		(x=0)	(x=0)
а значит,
lim lim z (x, y)		= lim lim z (x, y)	= lim lim z (x, y)	= 0.
x→0 y→0	1	x→0 y→0 2	x→0 y→0 3

6. Повторные пределы

В свою очередь, другие внутренние пределы равны:

lim z1(x, y) = lim z2(x, y) = lim z3(x, y) = 0,
x→0				x→0				x→0
(y=0)				(y=0)				(y=0)
а значит,
lim lim z	1(	x, y	)	lim lim z	2(	x, y	)	lim lim z	3(	x, y	= 0.
y→0 x→0	1(		)	= y→0 x→0	2(		)	= y→0 x→0	3(		)

Напомним, что двойные пределы функций z1(x, y), z2(x, y) и z3(x, y), как следует из результатов примеров 4.3, 5.3 и 5.4, не существуют, прич¨ем пределы по направлениям, как показано в примере 5.3, имеют различные значения для разных лучей.

Пример 6.2. Найти двойной и повторные пределы в точке x0 = y0 = 0 функции

z(x, y) =	x sin y	,	y = 0;
	1
	0,		y = 0.

Решение. Чтобы вычислить двойной предел, воспользуемся оценкой

		1			\|x\|,
	x sin y				\|x\|,

а поскольку
	lim	\|	x	\|	= 0		,
	x→0	\|		\|	= 0
то в силу теоремы 4.1	y→0
то в силу теоремы 4.1					1
	lim x sin				1	= 0.
	lim x sin					= 0.
	x→0				y
	y→0

Рассмотрим теперь повторные пределы. Первый из них равен

y→0	(y→=0)		y		y→0
lim	lim x sin		1		= lim		0 = 0,
	x 0
а второй	x→0	(x→=0)				y
	x→0	(x→=0)				y
	lim	lim		x sin		1
	lim	lim		x sin
		y 0

не существует, поскольку при x = 0 не существует внутренний предел

lim x sin 1 .

y→0 y

(x=0)

Эти два примера показывают, что из существования и равенства повторных пределов не следует существование двойного предела (пример 6.1), а из существования двойного предела не следует существование и равенство повторных пределов (пример 6.2). Следующая теорема формулирует условия, при которых из существования двойного предела следует существование и равенство ему повторных пределов.

<<< < Предыдущая 1 2 34 / 194 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 > Следующая >>>

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

#
20.11.2019173.7 Кб47fizika_kolosha (1).docx
#
29.05.20152.91 Mб424Fizika_razrushenia_posobie.doc
#
26.09.2019266.37 Кб75fizika_shpory1.docx
#
01.05.202549.26 Кб14Fizkultura.docx
#
29.05.20153.19 Mб115Fiz_pl_Sbornik_zadach_tema_7.doc
#
29.05.20152.23 Mб57FNP.pdf
#
24.08.20194.27 Mб69Freon_Thermodinamic_diagrams_i_lgP.doc
#
29.05.20151.25 Mб37FTI_Lekcii_po_osnovam_fiziki_plazmy.pdf
#
16.09.20197.33 Mб547Full.doc
#
15.11.20194.13 Mб15Full.docx
#
25.03.2016519.27 Кб15g2.pdf