FNP

то точка x0 называется точкой строгого условного минимума (максимума).

Точки условного минимума и условного максимума называются точками

условного экстремума.

Аналогично определяются точки условного строгого экстремума.

29.2.Прямой метод отыскания точек условного экстремума

Прямой метод реализуется в том случае, если из системы связей (29.1) можно выразить m каких-либо переменных xi через остальные переменные. Если это уда¨ется, то, подставив вместо соответствующих переменных xi их выражения че-

рез остальные − переменных в функцию , получим функцию ¯ от

(n m) f0(x) f0

этих (n − m) переменных. В результате задача о нахождении точек условного экстремума функции f0(x) при наличии связей (29.1) сводится к задаче нахож-

дения обычного, т.е. безусловного, экстремума функции ¯ , зависящей от −

переменных.

f0 (n m)

Рассмотрим несколько примеров, когда прямой метод отыскания точек условного экстремума может быть реализован.

Пример 29.1. Найти точки условного экстремума функций

1) z = x2 + y2; 2) z = − x2 + y2; 3) z = x2; 4) z = x2 − y2

при условии x + y = 1.

Решение. Эти функции рассматривались в примере 24.1. Там было показано, что точка O(0, 0) является точкой строгого минимума для первой функции, строгого максимума для второй, точкой минимума (нестрогого) для третьей функции, а четвертая функция точек экстремума не имеет. Рассмотрим, как эти результаты изменятся при дополнительном условии x + y = 1. Для этого из уравнения связи x + y = 1 выразим переменную y:

и подставим е¨ в уравнения функций. В результате получим функции z одной переменной и задача свед¨ется к отысканию безусловного экстремума этих функций. Итак, для функции z = x2 + y2 = x2 − (1 − x)2 = 1 − 2x − 2x2 найд¨ем z = −2 + 4x, z = 4. Тогда из равенства z = −2(1 − 2x) = 0 найд¨ем одну стационарную точку x0 = 1/2, которая в силу неравенства z = 4 > 0 является точкой строгого минимума. Из уравнения связи (29.4) найд¨ем y0 = 1 −x0 = 1 −1/2 = 1/2. Таким образом, мы нашли точку условного строгого минимума P (1/2, 1/2), в ко-

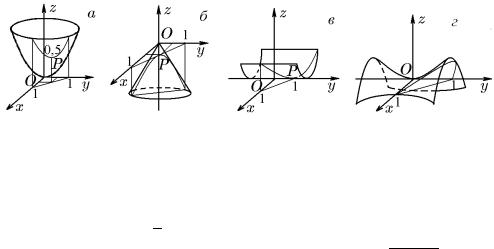
торой zmin = z(1/2, 1/2) = (1/2)2 + (1/2)2 = 1/2. Геометрически она соответствует вершине параболы, которая является линией пересечения параболоида вращения

Рис. 23.

3) Для функции z = x найд¨ем z = 2x, z = 2. Из равенства z = 2x = 0 имеем одну стационарную точку x0 = 0, которая в силу неравенства z = 2 > 0 является точкой строгого минимума. Из уравнения связи (29.4) найд¨ем y0 = 1 − x0 = 1. Таким образом, имеем точку условного строгого минимума P (0, 1), в которой zmin = z(0, 1) = 0. Геометрически она соответствует вершине параболы, которая является линией пересечения параболического цилиндра z = x2 с плоскостью x + y = 1 (рис. 23,в).

4) Для функции z = y2 − x2 = (1 − x)2 − x2 = 1 − 2x найд¨ем z = −2, z = 0. Отсюда в силу z = −2 = 0 следует, что функция z = 1 − 2x стационарных точек не имеет, а значит, и функция z = y2 − x2 не имеет условных экстремумов. Геометрически это означает, что линия пересечения гиперболического параболоида с плоскостью x + y = 1 экстремальных точек не имеет (рис. 23,г).

Решение. Из уравнения связи найд¨ем выражение для z: z = 1−x−y и подставим его в уравнение (29.5). Тогда

Таким образом, задача об отыскании условного экстремума для функции (29.5) свелась к нахождению безусловного экстремума функции двух переменных (29.7). Поскольку

wx = 4x, wy = 4y, wxx = 4, wxy = 0, wyy = 4,

то из уравнений

wx = 4x = 0, wy = 4y = 0

найд¨ем одну стационарную точку P (0, 0). Для выяснения е¨ характера выпишем коэффициенты

a11 = wxx = 4 > 0, a12 = wxy = 0, a22 = 4; δ = a11a22 − a212 = 16 > 0.

Отсюда следует, что точка P (0, 0) является точкой строгого минимума, а, значит, точка с координатами x = 0, y = 0, z = 1 является точкой условного строгого минимума функции (29.5) с wmin = w(0, 0, 1) = −1.

Пример 29.3. Исследовать на условный экстремум функцию

z = x2 + y2 − 12x + 16y

при условии x2 + y2 = 25.

Решение. Для этой функции в примере 28.2 мы нашли наибольшее и наименьшее значения в замкнутой области x2 +y2 25. Там же было показано, что на границе x2 + y2 = 25 функция имеет две экстремальные точки: P1(3, 4) — точка строгого минимума и P2(−3, 4) — точка строгого максимума. Следовательно, эти же точки будут точками строгого условного экстремума исследуемой функции.

29.3.Метод множителей Лагранжа

Прямой метод нахождения условного экстремума редко бывает эффективным, поскольку в этом случае необходимо разрешить уравнения связи (29.1) относительно какой-либо группы переменных. Последнее далеко не можно сделать в явном виде, поэтому перейд¨ем к изучению методов, позволяющих найти условный экстремум, не учитывая явного вида уравнений связи.

Для решения задачи об отыскании условного экстремума функции f0(x), x Rn, при наличии связей

воспользуемся методом Лагранжа, для чего введ¨ем вспомогательную функцию.Функция

жителями Лагранжа.

С помощью функции Лагранжа (29.9) задача об отыскании условного экстремума функции f0(x) со связями (29.8) сводится к исследованию на обычный

называется матрицей Якоби системы функций fi(x), i = 1, m, задающих уравнения связей (29.8).

Обозначим через D0 линейное многообразие в Rn:

означает, что dx = (dx1, ..., dxn) D0.

Сформулируем без доказательства достаточное условие существования условного экстремума.

Теорема 29.1. Пусть функции f0(x) и fi(x), i = 1, m, имеют непрерывные частные производные второго порядка в окрестности некоторой точки x0 Rn [т.е.

1)положительно определ¨енной, то x0 есть точка условного строгого минимума функции f0(x) при наличии связей (29.8);

2)отрицательно определ¨енной, то x0 есть точка условного строгого максимума функции f0(x) при наличии связей (29.8);

3)неопредел¨енной, то x0 не является точкой условного экстремума функции f0(x) при наличии связей (29.8).

Пример 29.4. Исследовать на условный экстремум функцию w = (x1)4 + ... + (xn)4,

если x1 + ... + xn = n.

Решение. Следуя (29.9), составим функцию Лагранжа

и запишем для не¨ систему (29.10) для нахождения стационарных точек:

n

∂L∂λ = xj − n = 0.

j=1

Из первых n уравнений этой системы найд¨ем

Так как квадратичная форма (29.14) является положительно определ¨енной, то точка x = (1, ..., 1) является точкой условного строгого минимума функции с

wmin = w(1, ..., 1) = n.

Пример 29.5. Найти экстремумы функции

w = x − 2y + 2z

на сфере x2 + y2 + z2 = 1.

Решение. Следуя (29.9), составим функцию Лагранжа

L(x, y, z, λ) = x − 2y + 2z + λ(x2 + y2 + z2 − 1)

и запишем для не¨ систему (29.10) для нахождения стационарных точек:

∂L∂λ = x2 + y2 + z2 − 1 = 0.

Из первых тр¨ех уравнений этой системы найд¨ем

Таким образом, функция Лагранжа имеет две стационарные точки: P1 = (M1, λ1) =

(M1, 3/2), M1 = (x1, y1, z1) = (−1/3, 2/3, −2/3) и P2 = (M2, λ2) = (M2, −3/2),

M2 = (x2, y2, z2) = (1/3, −2/3, 2/3). Так как

d2L = 2λ(dx2 + dy2 + dz2)

и в точке P1

d2L(P1) = 3(dx2 + dy2 + dz2) > 0,

а в точке P2

d2L(P2) = −3(dx2 + dy2 + dz2) < 0,

то точка M1(−1/3, 2/3, −2/3) — точка строгого условного минимума функции w, а точка M2(1/3, −2/3, 2/3) — точка строгого условного максимума функции w, прич¨ем wmin = w(P1) = −3, wmax = w(P2) = 3.

Пример 29.6. Найти условный экстремум функции

w = xy + yz,

если уравнения связей для x > 0, y > 0, z > 0 имеют вид

x2 + y2 = 2, y + z = 2.

Решение. Следуя (29.9), составим функцию Лагранжа

Отсюда λ1 = −1/2, λ2 = −1 и, соответственно, x = y = z = 1. Так как

d2L = 2λ1(dx2 + dy2) + 2dx dy + 2dy dz,

то

d2L(1, 1, 1, −1/2) = −dx2 − dy2 + 2dx dy + 2dy dz.

Из уравнений связи при x = y = z = 1 следует dy = −dz = −dx, поэтому d2L(1, 1, 1, −1/2) = −dx2 − 3dy2 − 2dz2 < 0.

Таким образом, в точке M(1, 1, 1) функция w имеет строгий условный минимум, равный wmin = 2.

найти пару наиболее близких друг к другу точек.

Решение. Во избежание путаницы координаты второй прямой будем обозначать прописными буквами X, Y, Z. Как известно, расстояние l от точки P1(x, y, z) первой прямой до точки P2(X, Y, Z) второй прямой находится по формуле

l = (X − x)2 + (Y − y)2 + (Z − z)2.

Оно будет наименьшим, если будет наименьшей величина

Таким образом, мы имеем задачу о нахождении экстремума функции (29.16) при условиях связи (29.15), которые можно записать в виде

2x − y − 5 = 0, 2x − z − 3 = 0, 3X − 2Y + 5 = 0, X − 2Z + 5 = 0.

+λ2(2x − z − 3) + μ1(3X − 2Y + 5) + μ2(X − 2Z + 5)

изапишем для не¨ систему (29.10) для нахождения е¨ стационарных точек:

Таким образом, в расширенном пространстве функция Лагранжа имеет одну стационарную точку, эквивалентную двум точкам в исходном пространстве:

В точках P1 и P2 функция (29.16) достигает условного экстремума. Выполнение достаточного условия в данном случае проверять нет необходимости, поскольку из постановки задачи очевидно, что это минимум.

Таким образом, точки P и P являются наименее удал¨енными точками пря-

1 2 √

мых (29.15) c наименьшим между ними расстоянием lmin = |P1P2| = 17/ 26. Этот результат легко проверяется методами аналитической геометрии (см.,

например, [10]). Из уравнений прямых имеем координаты их направляющих векторов и точек, через которые они проходят:

s1 = (1, 2, 2), s2 = (2, 3, 1), M1(2, −1, 1), M2(−3, −2, 1).

12 2

det

√

что совпадает с найденным выше lmin = 17/ 26.

♦ С помощью условного экстремума задачу о нахождении наибольшего и наименьшего значений функции можно сформулировать в более общих предположениях.

Если функция f(x) дифференцируема в области D Rn и непрерывна на

замыкании D, то она достигает своего наибольшего и наименьшего значения или в стационарной точке, или в точке, принадлежащей границе области D.

Задачи на отыскание экстремумов функций как числовых, так и более общей природы, при наличии связей широко распространены. Теория экстремальных задач помимо классических приложений находит широкое применение в области новейших приложений. Метод множителей Лагранжа имеет обобщения на случаи, когда ограничения задаются системой равенств и неравенств при помощи недифференцируемых в обычном смысле функций. В конкретных приложениях множители Лагранжа имеют содержательную интерпретацию. Так, в физике они задают реакцию связей, в экономике — цены на продукцию производства и т.д. В настоящее время широко развиваются методы решения экстремальных задач с использованием современных электронных технологий.

Задания для самоконтроля

Теоретические вопросы

I.Понятие функции нескольких переменных

1.Понятие функции нескольких переменных. Геометрический смысл функции нескольких переменных. Привести примеры функции нескольких переменных. Способы задания функции нескольких переменных. Линии и поверхности уровня функции нескольких переменных.

2.Определение метрического пространства. Привести примеры метрических пространств. Аксиомы метрики. Неравенства Коши и неравенство Минковского.

3.Многомерные последовательности. Сходимость в метрическом пространстве. Сходящиеся и расходящиеся последовательности. Последовательности, сходящиеся к бесконечно удал¨енной точке. Свойства пределов последовательностей. Теорема об ограниченности сходящейся последовательности.

4.Теоремы о пределе суммы, произведения и частного двух последовательностей. Фундаментальные последовательности. Признак Коши сходимости числовой последовательности. Полные метрические пространства.

II.Предел и непрерывность функции нескольких переменных

5.Предел функции нескольких переменных. Определение предела функции по Гейне

ипо Коши. Критерий Коши существования предела функции. Теоремы о пределах. Теоремы о пределе суммы, произведения и частного двух функций.

6.Предел функции нескольких переменных в точке по множеству и по направлению. Способы вычисления предела функции по множеству. Повторные пределы. Теорема о связи кратных и повторных пределов.

7.Непрерывность функций нескольких переменных в точке и на множестве. Непрерывность суммы, произведения и частного функции нескольких переменных. Теорема о промежуточных значениях непрерывной функции. Теоремы о непрерывности обратной сложной функции. Теорема о переходе к пределу под знаком непрерывной функции.

III.Дифференцируемость функции нескольких переменных

8.Частные производные функции нескольких переменных. Геометрический смысл частных производных функции нескольких переменных.

9.Дифференцируемость функции нескольких переменных в точке. Теорема о дифференцируемости функции нескольких переменных в точке.

10.Необходимые и достаточные условия дифференцируемости функции нескольких переменных в точке.

11.Дифференцирование сложной функции нескольких переменных. Теорема о частных производных сложной функции. Полная производная.

12.Производная по направлению. Градиент функции нескольких переменных. Градиент суммы, произведения и частного функции нескольких переменных.

13.Дифференциал функции нескольких переменных. Полное приращение и полный дифференциал функции нескольких переменных. Правила дифференцирования. Теорема об инвариантности формы первого дифференциала функции нескольких переменных.

14.Формула конечных приращений Лагранжа. Применение полного дифференциала в приближ¨енных вычислениях.

15.Касательная к пространственной кривой. Касательная плоскость и нормаль к поверхности.