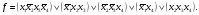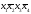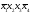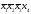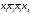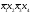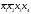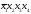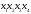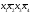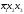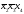8 выриант мат логика. 2 сем

Федеральное агентство по образованию

Государственное образовательное учреждение высшего профессионального образования

«ТОМСКИЙ ПОЛИТЕХНИЧЕСКИЙ УНИВЕРСИТЕТ»

Институт дистанционного образования

ИДЗ № 1

по дисциплине Математическая логика и теория алгоритмов

Вариант 8

Выполнил _{(подпись)}

студент гр. 3-8В22 Данилов К.В.

Курс 1 _(дата)

Проверил

преподаватель _{(подпись)}

_(дата)

Томск – 2013

Задание г) (диаграмм Эйлера – Венна.) не сделано, а так на 50 баллов

Таблица 1.

№	0	1	2	3	4	5	6	7	8	9	10	11	12	13	14	15
X1	0	1	0	1	0	1	0	1	0	1	0	1	0	1	0	1
X2	0	0	1	1	0	0	1	1	0	0	1	1	0	0	1	1
X3	0	0	0	0	1	1	1	1	0	0	0	0	1	1	1	1
X4	0	0	0	0	0	0	0	0	1	1	1	1	1	1	1	1
Y	0	0	0	0	0	1	1	0	1	1	1	0	1	0	1	1

Задание.

С полученной логической функцией Y выполнить следующие действия:

а) представить данную функцию в СДНФ, СКНФ и СПНФ;

б) минимизировать ее в СДНФ и СКНФ склеиванием;

в) минимизировать в СДНФ методом Куайна (Квайна);

г) проверить результаты минимизации с помощью диаграмм Эйлера – Венна.

Решение.

а) Любую булеву функцию y = f(a, b) можно представить как некоторую комбинацию областей:

Тогда, в зависимости от значения функции и заданных C_i, которые в этом случае называются конституентами, получим 16 логических операций:

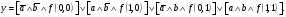
Подобная форма представления логических функций называется совершенной дизъюнктивной нормальной формой (СДНФ).

В логике Буля действует принцип двойственности, который гласит: при одновременной замене символов 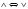и 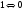все логические равенства остаются в силе. Поэтому СДНФ можно представить несколько иначе:

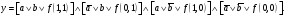
Эта форма представления называется совершенной конъюнктивной нормальной формой (СКНФ). Здесь уже конституенты представлены не в виде конъюнктов, как в СДНФ, а в виде дизъюнктов. Соединены же эти дизъюнкты конъюнкцией, отсюда и название — СКНФ.

Существует еще и третья форма — совершенная полиномиальная нормальная форма (СПНФ). Ее можно получить из СДНФ путем замены:

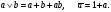
Поскольку конституенты не пересекаются 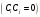, мы можем сразу же записать (в СПНФ символ конъюнкции опускается):

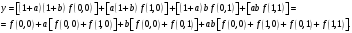
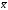У нас задана конкретная таблица истинности (табл. 1) для функции, зависящей от четырех аргументов. Тогда, выписывая соответствующие конъюнкты против единичных значений y, мы получим СДНФ. Если же мы выпишем дизъюнкты против нулевых значений y, то в результате уже получим СКНФ. Наконец, СПНФ образуется путем замены в СДНФ: на + и на (x + 1):

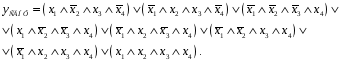
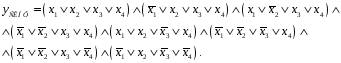
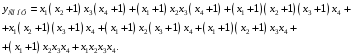
б) В логике Буля действует закон склеивания:

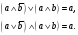
Применение этих законов позволяет найти более компактные аналитические выражения для заданной функции y, т.е. минимальную дизъюнктивную нормальную форму .

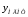Одну и ту же конституенту (импликанту) можно склеивать с другими конституентами (импликантами) многократно, так как в логике Буля действует закон идемпотентности:

поэтому любую конституенту можно размножить.

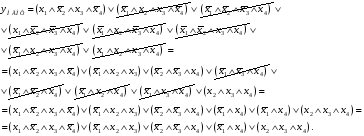
И для СКНФ, т.е. минимальную КНФ:

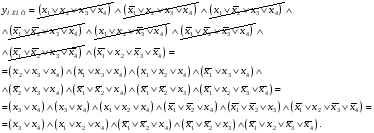
в) Для удобства изложения пометим каждую конституенту единицы из СДНФ функции f каким-либо десятичным номером (произвольно). Выполняем склеивания. Конституента 2 склеивается только с конституентой 7 (по переменной x₄), конституента 3 с конституентой 4 (по переменной x₁) и т. д. В результате получаем

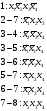
Заметим, что результатом склеивания является всегда элементарное произведение, представляющее собой общую часть склеиваемых конституент. Далее производим склеивания получаемых элементарных произведений.

Склеиваются только те произведения, которые содержат одинаковые переменные. Имеет место два случая склеивания:

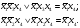
с появлением одного и того же элементарного произведения 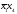. Дальнейшие склеивания невозможны. Произведя поглощения (из полученной ДНФ вычеркиваем все поглощаемые элементарные произведения), получим сокращенную ДНФ:

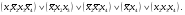
Переходим ко второму этапу. Для получения минимальной ДНФ необходимо убрать из сокращенной ДНФ все лишние простые импликанты. Это делается с помощью специальной импликантной матрицы Квайна.

Строки такой матрицы отмечаются простыми импликантами булевой функции, т. е. членами сокращенной ДНФ, а столбцы - конституентами единицы, т. е. членами СДНФ булевой функции.

Импликантная матрица имеет вид (таблица 2):

Таблица 2.

Простые импл.	Конституенты единицы
	×
		×					×
			×	×
			×		×	×	×
							×	×

Как уже отмечалось, простая импликанта поглощает некоторую конституенту единицы, если является ее собственной частью. Соответствующая клетка импликантной матрицы на пересечении строки (с рассматриваемой простой импликантой) и столбца (с конституентой единицы) отмечается крестиком (табл. 2). Дело в том, что конституента всегда может быть заменена импликантой или даже отдельным термом по закону поглощения:

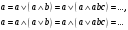
Минимальные ДНФ строятся по импликантной матрице следующим образом:

1. ищутся столбцы импликантной матрицы, имеющие только один крестик. Соответствующие этим крестикам простые импликанты называются базисными и составляют так называемое ядро булевой функции. Ядро обязательно входит в минимальную ДНФ.

2. рассматриваются различные варианты выбора совокупности простых импликант, которые накроют крестиками остальные столбцы импликантной матрицы, и выбираются варианты с минимальным суммарным числом букв в такой совокупности импликант.

Ядром нашей функции являются импликанты 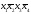, , 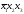, , 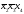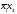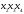. Поэтому функция имеет единственную тупиковую и минимальную ДНФ: