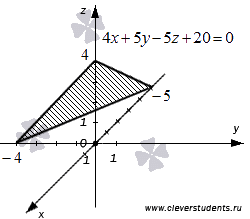Общее уравнение плоскости - основные сведения.

Сначала напомним, что понимается под фразой «уравнение плоскости в прямоугольной системе координат в трехмерном пространстве». Если в трехмерном пространстве задана прямоугольная система координат Oxyz, то уравнением плоскости в этой системе координат трехмерного пространства называют такое уравнение с тремя неизвестными x, y и z, которому удовлетворяют координаты всех точек плоскости и не удовлетворяют координаты никаких других точек. Иными словами, при подстановке координат некоторой точки плоскости в уравнение этой плоскости мы получим тождество, а при подстановке в уравнение плоскости координат какой-либо другой точки получится неверное равенство.

Прежде чем записать общее уравнение плоскости, напомним определение прямой перпендикулярной к плоскости: прямая перпендикулярна к плоскости, если она перпендикулярна любой прямой, лежащей в этой плоскости. Из этого определения следует, что любой нормальный вектор плоскости перпендикулярен любому ненулевому вектору, лежащему в этой плоскости. Этот факт мы используем при доказательстве следующей теоремы, которая задает вид общего уравнения плоскости.

Теорема.

Всякое уравнение вида , где A, B, C и D – некоторые действительные числа, причем А, В и C одновременно не равны нулю, определяет плоскость в заданной прямоугольной системе координат Oxyz в трехмерном пространстве, и всякая плоскость в прямоугольной системе координат Oxyz в трехмерном пространстве определяется уравнением вида при некотором наборе чисел A, B, C и D.

Доказательство.

Как видите, теорема состоит из двух частей. В первой части нам дано уравнение и нужно доказать, что оно определяет плоскость. Во второй части, нам дана некоторая плоскость и требуется доказать, что ее можно определить уравнением при некотором выборе чисел А, В, С и D.

Начнем с доказательства первой части теоремы.

Так как числа А, В и С одновременно не равны нулю, то существует точка , координаты которой удовлетворяют уравнению , то есть, справедливо равенство . Отнимем левую и правую части полученного равенства соответственно от левой и правой частей уравнения , при этом получим уравнение вида эквивалентное исходному уравнению . Теперь, если мы докажем, что уравнение определяет плоскость, то этим будет доказано, что эквивалентное ему уравнение также определяет плоскость в заданной прямоугольной системе координат в трехмерном пространстве.

Равенство представляет собой необходимое и достаточное условие перпендикулярности векторов и . Иными словами, координаты плавающей точки удовлетворяют уравнению тогда и только тогда, когда перпендикулярны векторы и . Тогда, учитывая факт, приведенный перед теоремой, мы можем утверждать, что если справедливо равенство , то множество точек определяет плоскость, нормальным вектором которой является , причем эта плоскость проходит через точку . Другими словами, уравнение определяет в прямоугольной системе координатOxyz в трехмерном пространстве указанную выше плоскость. Следовательно, эквивалентное уравнение определяет эту же плоскость. Первая часть теоремы доказана.

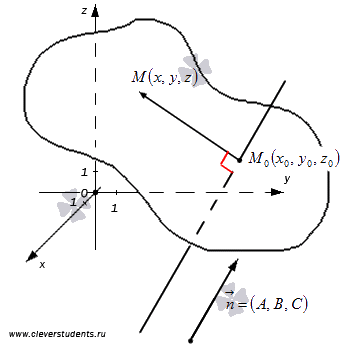
Приступим к доказательству второй части.

Пусть нам дана плоскость, проходящая через точку , нормальным вектором которой является . Докажем, что в прямоугольной системе координат Oxyz ее задает уравнение вида .

Для этого, возьмем произвольную точку этой плоскости. Пусть этой точкой будет . Тогда векторы и будут перпендикулярны, следовательно, их скалярное произведение будет равно нулю: . Приняв , уравнение примет вид . Это уравнение и задает нашу плоскость. Итак, теорема полностью доказана.

Уравнение называется общим уравнением плоскости в прямоугольной системе координат Oxyz в трехмерном пространстве.

Общее уравнение плоскости вида , где - некоторое действительное число, отличное от нуля, определяет в прямоугольной системе координат Oxyzплоскость, совпадающую с плоскостью , так как задает то же самое множество точек трехмерного пространства. К примеру, уравнения и задают одну и ту же плоскость, так как им удовлетворяют координаты одних и тех же точек трехмерного пространства.

Немного поясним смысл теоремы.

В заданной прямоугольной системе координат Oxyz плоскость и ее общее уравнение неразрывно связаны. То есть, каждой плоскости соответствует общее уравнение плоскости вида (при определенных значениях чисел А, В, С и D), а этому уравнению соответствует указанная плоскость в заданной прямоугольной системе координат в трехмерном пространстве.

Приведем пример, иллюстрирующий последнюю фразу.

Посмотрите на рисунок с изображением плоскости в трехмерном пространстве в фиксированной прямоугольной системе координат Oxyz. Этой плоскости соответствует уравнение , так как ему удовлетворяют координаты любой точки плоскости. С другой стороны, уравнение определяет в заданной системе координат Oxyzмножество точек, образом которого является изображенная на рисунке плоскость.