4 лаба по тау 2 семестр (ещё одна)

Министерство науки и образования Российской Федерации

Федеральное государственное бюджетное учреждение высшего

профессионального образования

«НАЦИОНАЛЬНЫЙ ИССЛЕДОВАТЕЛЬСКИЙ ТОМСКИЙ ПОЛИТЕХНИЧЕСКИЙ УНИВЕРСИТЕТ»

Институт – Энергетический институт

Направление – 140100 Теплоэнергетика и теплотехника

Кафедра – Автоматизации теплоэнергетических процессов

Исследование свойств нелинейной АСР

Отчет по лабораторной работе №6

по дисциплине «Теория автоматического управления»

Вариант №1

Выполнил: студент

группы 5Б03           С.С. Питер

Проверил: старший преподаватель

кафедры АТП                          Е.В. Иванова

                                                  

Томск – 2013

Цель работы: исследовать свойства нелинейных систем управления, получить навык расчетного определения параметров нелинейного регулятора (элемента), получить навык практического исследования нелинейных систем на ЭВМ.

Используемая в работе программа: AFX, NEL.

Постановка задачи:

Д

S

Y

Z

ля системы, представленной на рисунке 1,

Н.Э.

W_об

Рисунок 1 – Структурная схема нелинейной системы управления

с заданным видом нелинейности и передаточной функцией

расчетным методом определить параметры нелинейного элемента, обеспечивающего автоколебания с заданными параметрами на выходе АСР.

Исходные данные:

Передаточная функция объекта:

Параметры автоколебаний А=0,3 ; ω=0,08.

Порядок работы:

Условие устойчивости автоколебаний: если от точки пересечения ветвь характеристики при не охватывается АФЧХ линейной части, то автоколебания будут устойчивыми. Для определения параметров автоколебаний используется уравнение Гольдфарба: . Из которого видно, что параметры автоколебаний определяются в точке пересечения графиков АФЧХ объекта, и инверсной комплексной характеристики нелинейного элемента .

1 Для нелинейных элементов типа трехпозиционного реле, двухпозиционное реле, зоны нечувствительности, инверсная комплексная характеристика совпадает с действительной отрицательной полуосью, причем при инверсная комплексная характеристика нелинейного элемента , то есть параметры автоколебаний будут определяться в точке пересечения АФЧХ объекта и отрицательной вещественной полуоси. С помощью программы AFX строим АФЧХ объекта, график представлен на рисунке 2.

Таблица 1 – АФЧХ объекта

w	Re	Im	w	Re	Im
0,00	5,5	0	0,25	-0,313	0,249
0,01	5,046	-1,825	0,26	-0,275	0,252
0,02	3,900	-3,140	0,27	-0,239	0,252
0,03	2,509	-3,756	0,28	-0,207	0,251
0,04	1,238	-3,791	0,29	-0,178	0,247
0,05	0,249	-3,470	0,3	-0,151	0,243
0,06	-0,438	-2,987	0,31	-0,127	0,237
0,07	-0,875	-2,469	0,32	-0,105	0,230
0,08	-1,123	-1,980	0,33	-0,085	0,223
0,09	-1,242	-1,549	0,34	-0,067	0,216
0,10	-1,274	-1,184	0,35	-0,051	0,208
0,11	-1,251	-0,883	0,36	-0,036	0,199
0,12	-1,195	-0,637	0,37	-0,023	0,191
0,13	-1,121	-0,439	0,38	-0,011	0,182
0,14	-1,038	-0,280	0,39	0,000	0,174
0,15	-0,952	-0,153	0,4	0,010	0,165
0,16	-0,868	-0,053	0,41	0,019	0,157
0,17	-0,786	0,025	0,42	0,027	0,148
0,18	-0,710	0,087	0,43	0,033	0,140
0,19	-0,638	0,135	0,44	0,040	0,132
0,20	-0,571	0,171	0,45	0,045	0,124
0,21	-0,510	0,199	0,46	0,050	0,116
0,22	-0,454	0,219	0,47	0,054	0,108
0,23	-0,403	0,234	0,48	0,058	0,101
0,24	-0,356	0,244	0,49	0,061	0,094

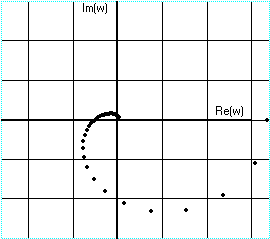
Рисунок 2 - АФЧХ линейной части системы

По АФЧХ определяем параметры автоколебаний, возможных в данной системе:

A_вых= 0,8694699;

ω_вых = 0,16.

Рассчитанная ω_вых не совпадает с заданной.

Автоколебания с заданными параметрами в системе с нелинейными элементами типа трехпозиционного реле, двухпозиционное реле, зоны нечувствительности невозможны, т.к. параметры автоколебаний, находящиеся на пересечении графиков АФЧХ объекта и инверсной комплексной характеристики нелинейного элемента отличаются от заданных.

2 Определение параметров автоколебаний для трёх позиционного реле с зоной нечувствительности и зоной возврата;

Строим АФЧХ линейной части. Для разных значений параметров нелинейного элемента строим АФЧХ инверсной комплексной характеристики нелинейного элемента. При различных параметрах нелинейного элемента не удалось добиться совпадения частоты и амплитуды автоколебаний с заданными.

Следовательно, автоколебания при заданных значениях частоты и амплитуды не возможны.

Приведем график при следующих параметрах: b = 0,029; c = 0,01 ; m = 0,1

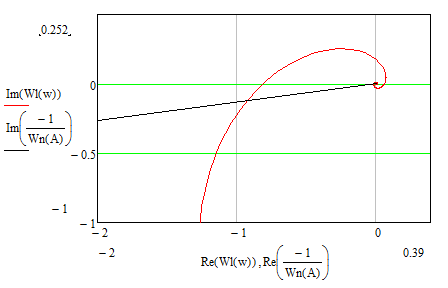
Рисунок 3 – АФЧХ линейной и нелинейной части системы

По рисунку 2 определяем параметры автоколебаний, возможных в данной системе:

ω_вых = 0,16 с^-1 ; A_вых= 0,8694699;

ВЫВОД

Автоколебания с заданными параметрами в системе с нелинейными элементами типа двух-, трехпозиционное реле, трёх позиционного реле с зоной нечувствительности и зоной возврата невозможны, т.к. параметры автоколебаний, находящиеся на пересечении графиков АФЧХ объекта и инверсной комплексной характеристики нелинейного элемента отличаются от заданных.

5