
Лабораторная работа Оценка закона распределения на основе выборочных данных.
Цель работы:
Оценка закона распределения генеральной совокупности на основе выборочных данных..
Задание.
Имеется выборка объемом
![]() из неизвестного распределения
из неизвестного распределения
![]() (приложение 3). Предполагается, что
(приложение 3). Предполагается, что
![]() может быть одним из следующих распределений:
может быть одним из следующих распределений:
1)
![]() - нормальное распределение с плотностью
- нормальное распределение с плотностью
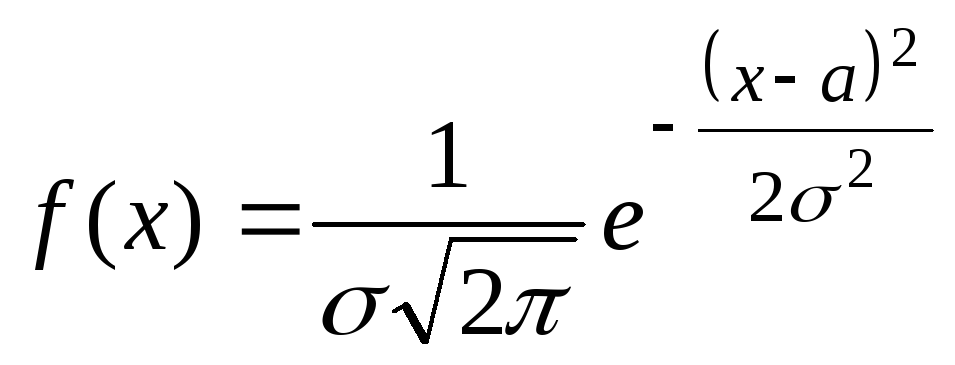 ,
,
![]() ,
где параметры
,
где параметры
![]() и
и
![]() - неизвестны;
- неизвестны;
2)
![]() - распределение Лапласа с плотностью
- распределение Лапласа с плотностью
![]() ,
,
![]() ,
где параметры
,
где параметры
![]() и
и
![]() - неизвестны;
- неизвестны;
3)
![]() - распределение Коши с плотностью
- распределение Коши с плотностью
![]() ,
,
![]() ,
где параметры
,
где параметры
![]() и
и
![]() - неизвестны;
- неизвестны;
4)
![]() - показательное распределение с плотностью
- показательное распределение с плотностью
![]() ,
,
![]() ,
где параметр
,
где параметр
![]() - неизвестен;
- неизвестен;
5)
![]() - распределение Релея с плотностью
- распределение Релея с плотностью
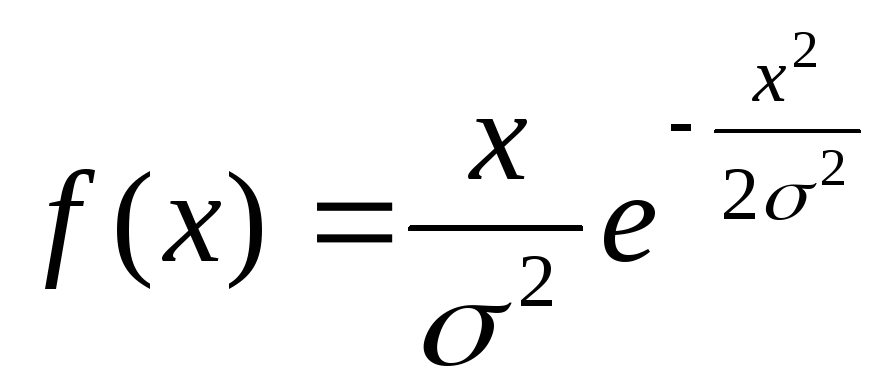 ,
,
![]() ,
где параметр
,
где параметр
![]() - неизвестен;
- неизвестен;
-
 - распределение с плотностью
- распределение с плотностью
 ,
,
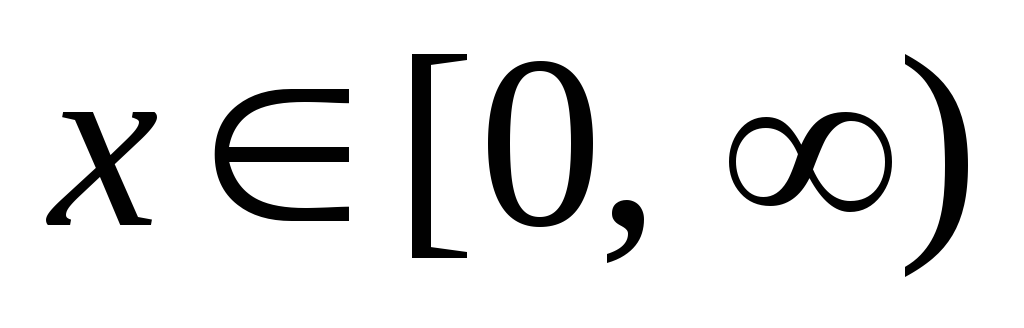 ,
где параметр
,
где параметр
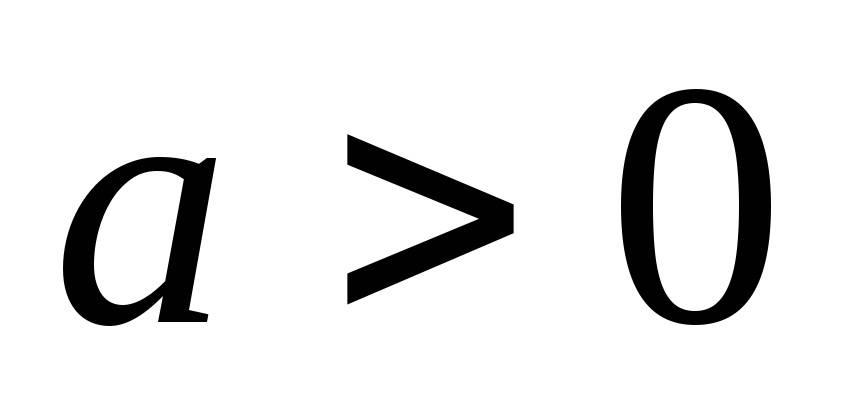 неизвестен.
неизвестен. -
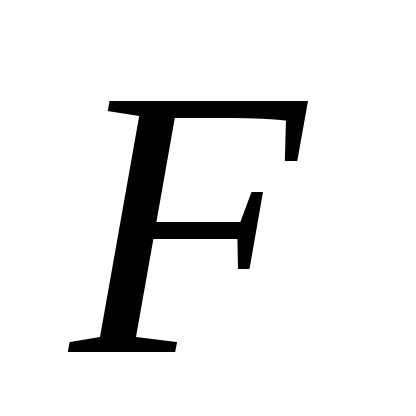 - распределение хи-квадрат с с плотностью
- распределение хи-квадрат с с плотностью
 ,
где параметр
,
где параметр
 неизвестен.
неизвестен.
Требуется:
-
Представить выборку в виде интервального статистического ряда. При разбивке на интервалы следует следить за тем, чтобы частоты
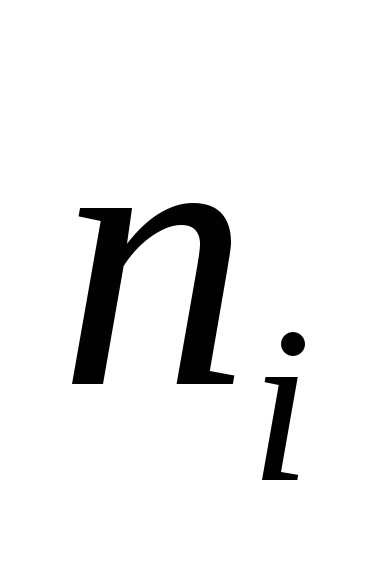 для всех интервалов были одного порядка,
причем количество выборочных значений
для всех интервалов были одного порядка,
причем количество выборочных значений
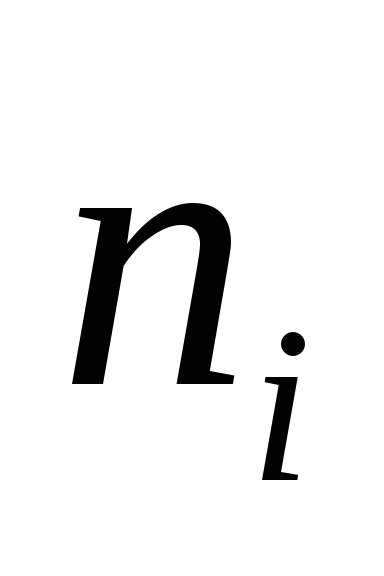 попавших в каждый интервал должно быть
не меньше 5 (
попавших в каждый интервал должно быть
не меньше 5 ( ).
В противном случае следует изменять
длины интервалов, добиваясь относительно
равномерного распределения частот по
интервалам.
).
В противном случае следует изменять
длины интервалов, добиваясь относительно
равномерного распределения частот по
интервалам.
-
Построить гистограмму и сравнить ее (качественно) с кривыми плотности возможных теоретических распределений.
-
Выдвинуть гипотезу
 о виде закона распределения (на основе
сравнения гистограммы с графиком
плотности теоретического распределения).
Используя критерий Пирсона на уровне
значимости
о виде закона распределения (на основе
сравнения гистограммы с графиком
плотности теоретического распределения).
Используя критерий Пирсона на уровне
значимости
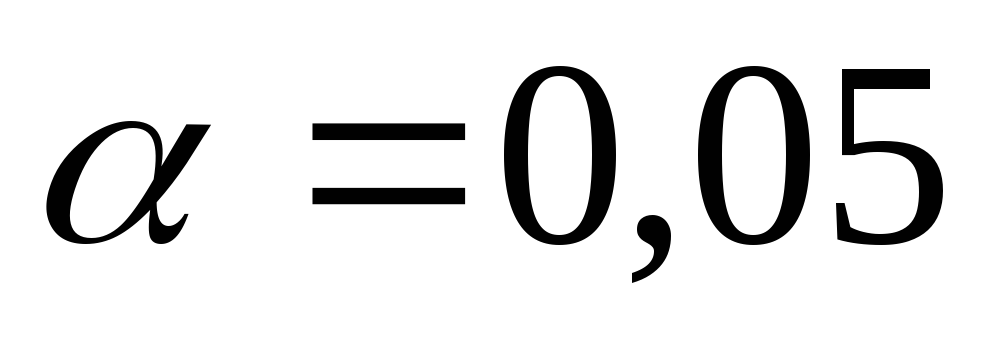 проверить гипотезу
проверить гипотезу
 .
Если гипотеза отвергается, следует
выдвинуть другую и аналогично подвергнуть
ее проверке.
.
Если гипотеза отвергается, следует
выдвинуть другую и аналогично подвергнуть
ее проверке. -
Для принятой гипотезы уточнить значение оценок параметров распределения, используя метод наименьших квадратов (определяем оценки, исходя из минимума статистики критерия Пирсона
 )
) -
Найти реально достигнутый уровень значимости
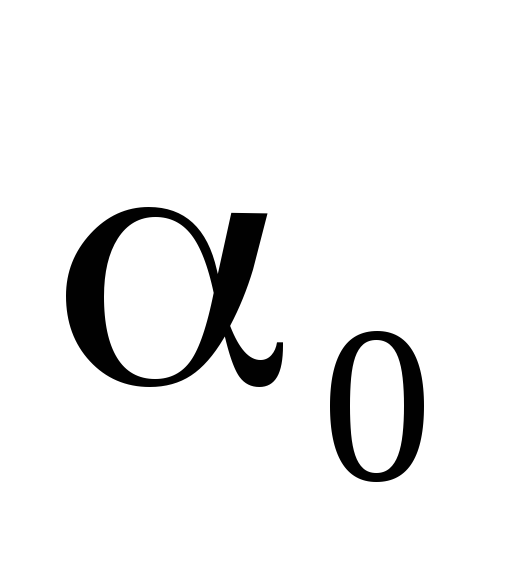 ,
то есть вероятность того, что при
истинности гипотезы
,
то есть вероятность того, что при
истинности гипотезы
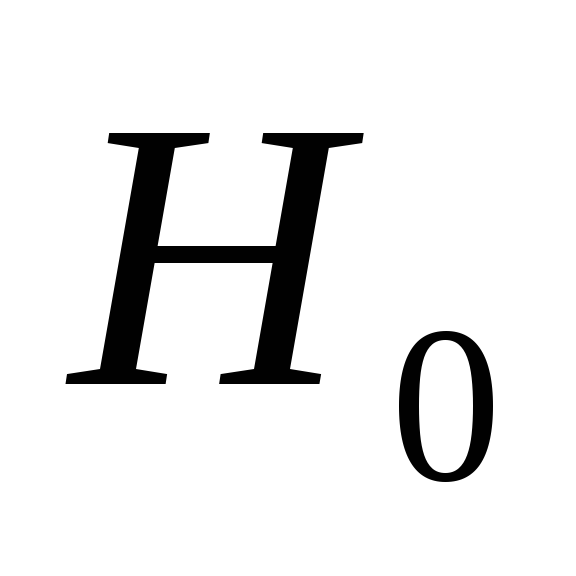 значение статистики
значение статистики
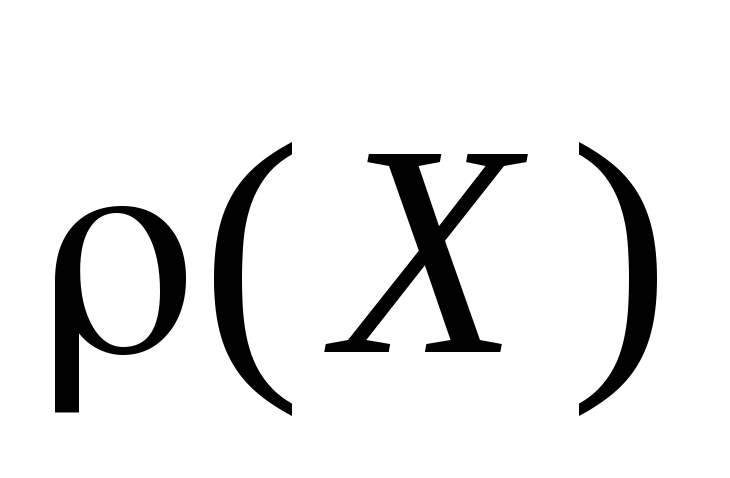 будет больше наблюдаемого значения
статистики
будет больше наблюдаемого значения
статистики
 :
:
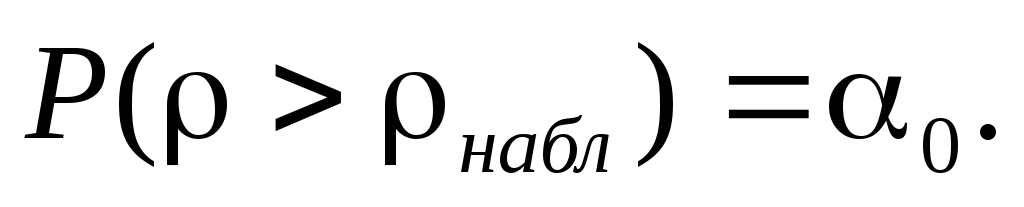
Приложение 1.
Критерий (Пирсона) для простой гипотезы
Пусть
![]() выборка из генеральной совокупности
выборка из генеральной совокупности
![]() .
Проверяется гипотеза
.
Проверяется гипотеза
![]() против альтернативы
против альтернативы
![]() .
.
Представим выборку
в виде группированного ряда, разбив
предполагаемую область значений
случайной величины на
![]() интервалов. Пусть
интервалов. Пусть
![]() - число элементов выборки попавших в
- число элементов выборки попавших в
![]() -ый
интервал, а
-ый
интервал, а
![]() - теоретическая вероятность попадания
в этот интервал при условии истинности
- теоретическая вероятность попадания
в этот интервал при условии истинности
![]() .
Составим статистику
.
Составим статистику
![]() ,
которая характеризует сумму квадратов
отклонения наблюдаемых значений
,
которая характеризует сумму квадратов
отклонения наблюдаемых значений
![]() от ожидаемых
от ожидаемых
![]() по всем интервалам группирования.
по всем интервалам группирования.
Теорема Пирсона.
Если
![]() верна, то при фиксированном
верна, то при фиксированном
![]() и
и
![]()
![]() . (1)
. (1)
Таким образом,
статистику
![]() можно использовать в качестве статистики
критерия согласия для проверки гипотезы
о виде закона распределения, который
будет иметь вид:
можно использовать в качестве статистики
критерия согласия для проверки гипотезы
о виде закона распределения, который
будет иметь вид:
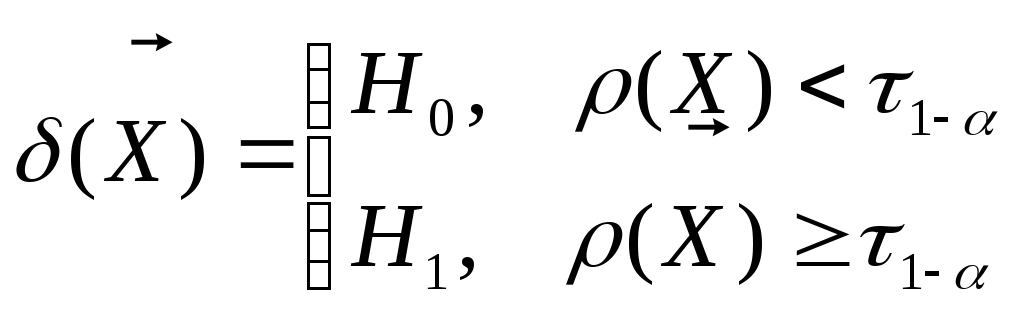 ,
,
![]() , (2)
, (2)
где
![]() -квантиль
распределения
-квантиль
распределения
![]() .
.
Данный критерий
называется критерием
![]() или критерием согласия Пирсона.
или критерием согласия Пирсона.
Замечание.
Критерий не состоятелен для альтернатив,
для которых
![]() для всех
для всех
![]() .
Поэтому, следует стремиться к как можно
большему числу интервалов группирования.
Однако, с другой стороны, сходимость к
.
Поэтому, следует стремиться к как можно
большему числу интервалов группирования.
Однако, с другой стороны, сходимость к
![]() величины
величины
![]() обеспечивается ЦПТ, то есть ожидаемое
значение
обеспечивается ЦПТ, то есть ожидаемое
значение
![]() для каждой ячейки не должно быть слишком
мало. Поэтому обычно число интервалов
выбирают таким образом, чтобы
для каждой ячейки не должно быть слишком
мало. Поэтому обычно число интервалов
выбирают таким образом, чтобы
![]() .
.
