Лабораторная работа 3_MAPLE_2012

ФЕДЕРАЛЬНОЕ АГЕНТСТВО ПО ОБРАЗОВАНИЮ

Государственное образовательное учреждение высшего профессионального образования

«ТОМСКИЙ ПОЛИТЕХНИЧЕСКИЙ УНИВЕРСИТЕТ»

УТВЕРЖДАЮ

Заместитель

директора по

учебной работе

_____________С.А. Гайворонский

«___» ___________________2012г.

Практикум на ЭВМ

Методические указания к выполнению лабораторной работы №3

«ОРГАНИЗАЦИЯ ЦИКЛИЧЕСКИХ ВЫЧИСЛЕНИЙ

И ПОСТРОЕНИЕ РЯДОВ В ПАКЕТЕ MAPLE»

для студентов направления 510200 «Прикладная математика и информатика»

Томск 2012 г.

УДК 681.3; 517.9

Практикум на ЭВМ.

Методические указания к выполнению лабораторной работы №3 «Организация циклических вычислений и построение рядов в пакете MAPLE» для студентов направления 510200 «Прикладная математика и информатика».

Томск: Изд. ТПУ, 2011. –11 с.

Составил: доц., к.т.н. А.В. Козловских

Рецензент: доц. к.ф.-м.н. Г.Е. Шевелёв

Методические указания рассмотрены и рекомендованы к изучению методическим семинаром кафедры Прикладной математики.

«____» __________2012 г.

Зав. кафедрой ПМ

проф., д. ф.-м. н. _______________ В.П.Григорьев

ЛАБОРАТОРНАЯ РАБОТА №3

ОРГАНИЗАЦИЯ ЦИКЛИЧЕСКИХ ВЫЧИСЛЕНИЙ И ПОСТРОЕНИЕ РЯДОВ

Цель работы:

Изучение функций математического анализа пакета MAPLE и освоение методики построения рядов с использованием этих функций.

В разделе пакета «Функции математического анализа» дается перечень функций, позволяющих решать широкий круг задач традиционно относящихся к математическому анализу. Количество их огромно, поэтому рассмотрим только те из них, которые необходимы для выполнения лабораторной работы.

Основные формулы для вычисления сумм последовательностей

Начнем рассмотрение таких операций с вычисления сумм последовательностей. Вычисление суммы членов некоторой последовательности f(k) при изменении целочисленного индекса k от значения m до значения n с шагом +1, то есть выражения:

sum(f, k) sum(f, k=m..n) sum(f, k=alpha) sum(f, k=expr)

Sum(f, k) Sum(f, k=m..n) Sum(f, k=alpha) Sum(f, k=expr)

Здесь f — функция, задающая члены суммируемого ряда, k — индекс суммирования, тип — целочисленные пределы изменения k, alpha — RootOf-выражение. Значение n может быть равно бесконечности. В этом случае для n используется обозначение ? или infinity. Функции, начинающиеся с большой буквы, не выполняют вычисления, а только записывают аналитическое выражение:

> Sum(k^2,k=1..4);

>sum(k^2,k=1..4); 30

Суммы бесконечных последовательностей

Многие суммы бесконечных последовательностей сходятся к определенным численным или символьным значениям, и система Maple способна их вычислять. Это поясняют следующие примеры:

>restart;

>sum(-exp(-k),k);

>sum(k*a^k,k);

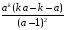
>sum(1/k!,k=0..infinity); e

>Sum(1/i^2,i=1..infinity)= sum(1/i^2,i=1..infinity);

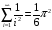
>Sum(1/n!,n=1..infinity)= sum(1/n!,n=1..infinity);

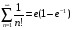
>evalf(%);

Заметим, что команда evalf(%), применяется к предыдущему результату (см. в последнем примере).

Двойные суммы

Могут встречаться множественные суммы по типу «сумма в сумме». Ограничимся приведением примера двойной суммы, имеющей аналитическое значение:

>Sum(Sum(k^2,k=1..m),m=1..N);factor(simplify(value(%)));

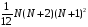
> subs( N = 100, %); 8670850

Команда subs – подстановка указанного значения N в предыдущий результат (знак %).

Разложение в ряды Тейлора и Маклорена

Для разложения в ряд Тейлора используется функция taylor(expr, eq/nm, n). Здесь ехрr — разлагаемое в ряд выражение, eq/nm — равенство (в виде х=а) или имя переменной (например, х), n — необязательный параметр, указывающий на порядок разложения и представленный целым положительным числом (при отсутствии указания порядка он по умолчанию принимается равным 6). При задании eq/nm в виде х=а разложение производится относительно точки х =а. При указании eq/nm в виде просто имени переменной разложение ищется в окрестности нулевой точки, то есть фактически вычисляется ряд Маклорена.

>taylor(1-exp(x),x=1,4);

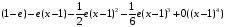
>convert(%,polynom);

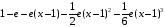
>taylor(sinh(x),x,10);

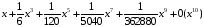
>taylor(erf(x),x);

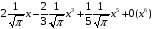
Для разложения в ряд Тейлора функций нескольких переменных, используется библиотечная функция mtaylor:

mtaylor(f, v); mtaylor(f, v, n); mtaylor(f, v, n, w).

Здесь f — алгебраическое выражение, v — список имен или равенств, n — необязательное число, задающее порядок разложения, w — необязательный список целых чисел, задающих «вес» каждой из переменных списка v. Эта функция должна вызываться из библиотеки Maple с помощью команды readlib:

>readlib(mtaylor);

proc()…end proc

>mtaylor(sin(x*y),[x,y]10,[2,1]);

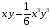
>mtaylor(exp(-x)*sin(y),[x,y],5);

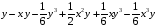
Ход работы:

Предварительно изучив функции, решить следующие задачи в пакете MAPLE.

1. Разложить функцию 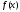в ряд Тейлора в точке 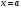. Число членов ряда .

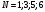2. Разложить в ряд Фурье функцию 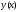, заданную таблицей значений 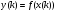на периоде T с шагом .

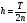При этом: 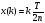; ; 2n – число шагов сетки; (2n+1) – число узлов сетки.

Исходные данные к задаче: вектор значений функции Y; n; T.

Ряд Фурье для таких функций представляется выражением:

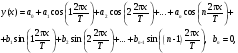(1)

где коэффициенты необходимо найти как функции от y(k); n; T.

Разделим задачу на следующие этапы:

а) используя функции пакета SUM, вычислить 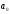по выражению

.

б) используя функции пакета SUM и оператор цикла, вычислить 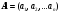, по следующим аналитическим выражениям:

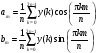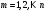, для . (2)

в) получить (с использованием функций SUM) аналитическое выражение для ряда (1) с вычисленными коэффициентами 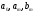и заданными значениями n и T.

Построить на одном графике по полученному выражению (1) на интервале T и на этом же интервале построить график по заданным точкам (Y[i],x[i]).

Графики функций, построенные точками

В следующем примере переменная Р имеет вид списка, в котором попарно перечислены координаты точек функции sin(x).

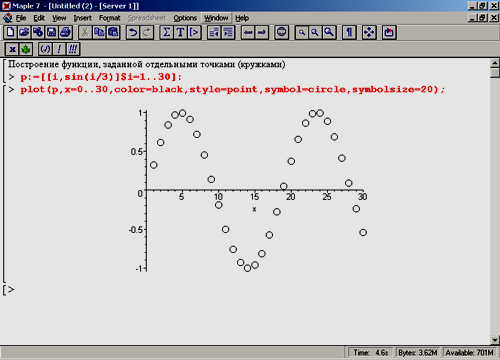
Рис.1. график точек в виде (О)

В этом нетрудно убедиться, заменив знак «:» после выражения, задающего Р, на знак «;». Далее по списку Р построен график точек в виде (О), которые отображают отдельные значения функции sin(x).

Контрольные вопросы

1. Какие параметры являются входными для функции TAYLOR?

2. В чем отличие между разными функциями SUM?

3. Какие функции входят в раздел «Функции математического анализа»?

4. Как по заданному аналитическому выражению 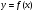, вычислить 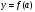(т.е. в точке ).

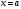Индивидуальные задания

1.

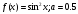
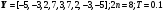
2.

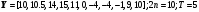
3.

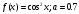
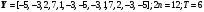
4.

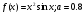
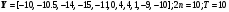
5.

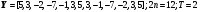
6.

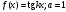
7.

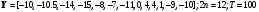
8.

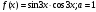
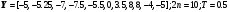
9.

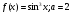
10.

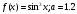
11.

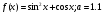
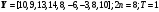
12.

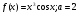
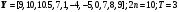
13.

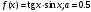
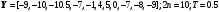
14.

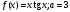
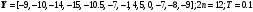
15.

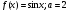
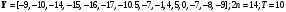
16.

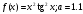
17.

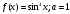
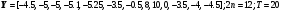
18.

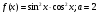
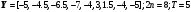
19.

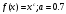
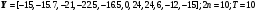
20.

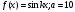
21.

22.

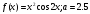
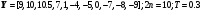
23.

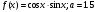
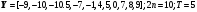
24.

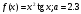
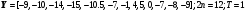
Пример

> with(linalg):

> n:=5; n:=5

> T:=2; T:=2

> Y:=<-4.5 |-5| -5.25 | -3.5 | -0.5 | 8 | 10 | 0 | -3.5|-4|-4.5>;

> x1:=<0|0.2 |0.4|0.6|0.8|1.|1.2|1.4|1.6|1.8|2.>;

> type(Y,vector);

false

> V:=convert(Y,vector);

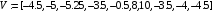
> a0:=1/(2*n)*sum(V[j],j=1..10);

> type(x1,vector);

false

> x2:=convert(x1,vector);

> a:=array(1..5);

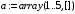
> for m to 5 do a[m]:=1/n*sum(V[k+1]*cos(k*m*3.14/n),k=0..(2*n-1))

od;

> type(a,vector);

false

> a1:=array(1..5,[-5.818559130,2.726342144,-.5136070478,-

-.1308651318,.1499321486]);

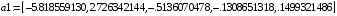> type(a1,vector); true

> b:=array(1..5); b:=array(1..5,[])

> for m to 5 do b[m]:=1/n*sum(V[k+1]*sin(k*m*3.14/n),k=0..(2*n-1)) od;

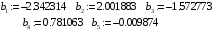
> b1:=array(1..5,[-2.342314932,2.001883446,-1.572773349,.7810631266,-

0.9874141256e-2]);

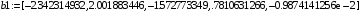>z(x):=a0+sum(a1[k]*cos(k*6.28*x/T),k=1..n)+sum(b1[k]*sin(k*6.28*x/

T),k=1..n);

+-

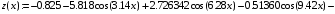
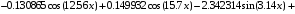
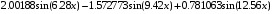> plot(z(x),x=0..2);

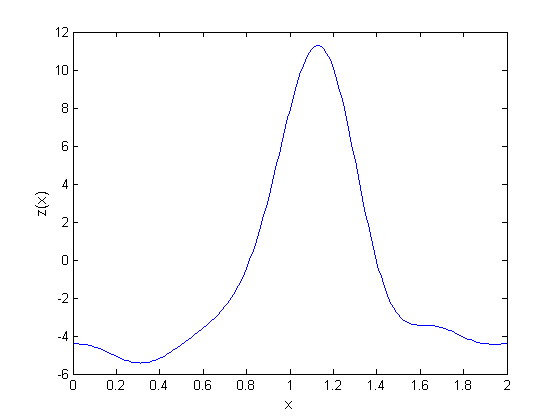
Рис.2. График функции ряда Фурье

> z1:=array(1..2,1..11,[[0, .2, .4, .6, .8, 1., 1.2, 1.4, 1.6, 1.8, 2.],[-4.5, -5, -5.25, -3.5, -.5, 8, 10, 0, -3.5, -4, -4.5]]);

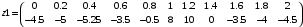
> z2:=transpose(z1);

> type(z2,matrix); true

> z3:=[[0, -4.5], [.2, -5], [.4, -5.25], [.6, -3.5], [.8, -.5], [1., 8], [1.2, 10], [1.4, 0], [1.6, -3.5], [1.8, -4], [2., -4.5]];

> plot(z3,x=0..2,color=blue,style=point,symbol=circle);

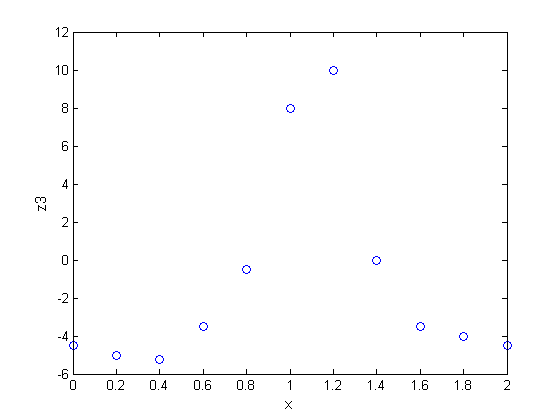
Рис.3. Исходные данные

Пример построения двух графиков. Здесь z(x) – ряд Фурье, z3 – исходные данные.Рис.4.

plot([z(x),z3],x=0..2,color=[blue,blue],style=[line,point],symbol=circle);

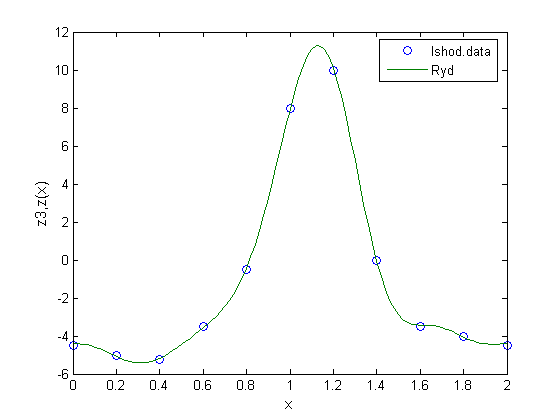
Рис.4. Пример построения двух графиков

Организация циклических вычислений и построение рядов в пакете MAPLE

Методические указания

по выполнению лабораторной работы

Составил:

Козловских Александр Владимирович

Подписано к печати

Формат 60х84.16. Бумага ксероксная.

Плоская печать. Усл. печ.л.. Уч.-изд. л

Тираж зкз. Заказ . Цена свободная.

ИПФ ТПУ. Лицензия ЛТ №1 от 18.07.2011.

Типография ТПУ. 634034, Томск, пр. Ленина, 30.