
Лабораторная работа 4_MAPLE_2012
.docxФЕДЕРАЛЬНОЕ АГЕНТСТВО ПО ОБРАЗОВАНИЮ

«НАЦИОНАЛЬНЫЙ ИССЛЕДОВАТЕЛЬСКИЙ ТОМСКИЙ ПОЛИТЕХНИЧЕСКИЙ УНИВЕРСИТЕТ»
УТВЕРЖДАЮ
Заместитель
директора по
учебной работе
_____________С.А. Гайворонский
«___» ___________________2012г.
Практикум на ЭВМ
Методические указания к выполнению лабораторной работы №4
«ИЗУЧЕНИЕ МЕТОДОВ РЕШЕНИЯ ОДНОРОДНЫХ ДИФФЕРЕНЦИАЛЬНЫХ УРАВНЕНИЙ С ПОСТОЯННЫМИ КОЭФФИЦИЕНТАМИ ПОРЯДКА N
В ПАКЕТЕ MAPLE»
для студентов направления 510200 «Прикладная математика и информатика»
Томск 2012 г.
УДК 681.3; 517.9
Практикум на ЭВМ.
Методические указания к выполнению лабораторной работы №4 «Изучение методов решения однородных дифференциальных уравнений с постоянными коэффициентами порядка N в пакете MAPLE» для студентов направления 510200 «Прикладная математика и информатика».
Томск: Изд. ТПУ, 2011. – 10 с.
Составил: доц., к.т.н. А.В. Козловских
Рецензент: доц., к.т.н. Г.Е. Шевелёв
Методические указания рассмотрены и рекомендованы к изучению методическим семинаром кафедры Прикладной математики.
«____» __________2012 г.
Зав. кафедрой ПМ
проф., д. ф.-м. н. _______________ В.П.Григорьев
ЛАБОРАТОРНАЯ РАБОТА №4
ИЗУЧЕНИЕ МЕТОДОВ РЕШЕНИЯ ОДНОРОДНЫХ ДИФФЕРЕНЦИАЛЬНЫХ УРАВНЕНИЙ
С ПОСТОЯННЫМИ КОЭФФИЦИЕНТАМИ ПОРЯДКА N
в пакете MAPLE
Цель работы:
Освоение методов построения аналитического решения дифференциальных уравнений (общего решения и задачи Коши) в пакете MAPLE.
Перечень вопросов по теории дифференциальных уравнений, подлежащих предварительному изучению.
1. Определение однородного дифференциального уравнения с постоянными коэффициентами.
2. Что такое характеристический полином и его корни?
3. Фундаментальная система решений и связь входящих в нее функций с корнями характеристического полинома.
4. Построение общего решения однородного уравнения.
5. Формулировка задачи Коши и ее решение.
Общее решение однородного уравнения
1. Записать характеристический полином для заданного уравнения и найти его корни.
2. Построить, в соответствии с найденными корнями, фундаментальную систему решений.
3. Записать общее решение однородного уравнения в виде:
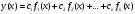 ,
,
где: n – порядок дифференциального уравнения;
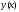 – общее
решение этого уравнения;
– общее
решение этого уравнения;
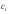 – произвольные
константы;
– произвольные
константы;
 – функции,
входящие в фундаментальную систему
решений;
– функции,
входящие в фундаментальную систему
решений;
x – независимая переменная.
4.
Для проверки правильности полученного
решения,
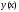 подставить в исходное дифференциальное
уравнение и убедиться, удовлетворяет
ли оно ему.
подставить в исходное дифференциальное
уравнение и убедиться, удовлетворяет
ли оно ему.
Подстановки с помощью функций subs и subsop
Прежде чем приступим к решению уравнения, познакомимся с этими функциями подстановки выражений.
Подстановки в общем случае служат для замены одной части выражения на другую. Частными видами подстановок являются такие виды операций, как замена одной переменной на другую или замена символьного значения переменной ее численным значением. Основные операции подстановки выполняют следующие функции:
-
subs(x=a,e) — в выражении е заменяет подвыражение х на подвыражение а;
-
subs(sl,...,sn,e) — в выражении е заменяет одни подвыражения на другие, выбирая их из списков si, ..., sn вида х=а;
-
subsop(eql, eq2, .... eqi, ...eqn, e) — в выражении е заменяет указанные в eqi операнды другими, указанными в правой части равенств eqi вида ni=ei, где ni — номер операнда, ei — выражение для замены.
Все эти функции возвращают измененное после подстановки выражение. Ниже показаны примеры применения функций подстановок:
>subs(a=b,b^2-2*a*b-b^2);
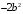
>subs(a=2,b=1,b^2-2*a*b-b^2);
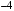
>subs(c=a-b,(a^2-2*a*b-b^2)/c);
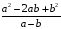
>normal(%);
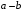
>subs(a=x,b=y,c=z,[a,b,c]);
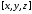
>subs({x=y,y=x},[x,y]);
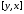
>subs(a=sin(x),b=cos(x),a^2+b*b);
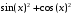
>simplify(%); 1
>subsop(1=x,a+b+c);
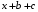
>subsop(2=x,a+b+c);
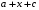
>subsop(3=x,a+b+c);

>subsop(1=sin(x),(1+cos(x))/b);
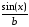
>subsop(2=sin(x),(1+cos(x))/b);
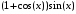
>subsop(1=sin(x),2=sin(x),(1+cos(x))/b);
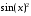
Следует обратить внимание на то, что результат подстановок, полученный с помощью функции subsop, порой может не совпадать с ожидаемым. Поэтому полезно контролировать получаемые в результате подстановок выражения на их корректность. Одним из важных применений подстановок является проверка правильности решений уравнений и систем уравнений. Ниже дан пример такой проверки:
>eqs:={x+y+z=6,y/x=z-1,z-x=2};
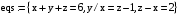
>res:=solve(eqs,{x,y,z});
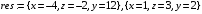
>subs(res,eqs);
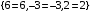
Решение заданного уравнения в пакете MAPLE
Данный пакет, позволяющий получить решение многих математических задач в символьном виде, является эффективным инструментом при изучении дифференциальных уравнений.
На
примере уравнения
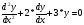 рассмотрим последовательность действий
и набор функций, необходимых для
выполнения пунктов 1-4 первого раздела.
рассмотрим последовательность действий
и набор функций, необходимых для
выполнения пунктов 1-4 первого раздела.
1.Запишем характеристический полином в текущей строке ввода по правилам пакета MAPLE:
> hp:=v^2+2*v+3;
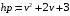
2. Для нахождения корней воспользуемся функцией solve.
В строке ввода запишем следующее выражение:
3.Для построения общего решения, сначала запишем вектор функций, образующих ФСР (в соответствии с типом найденных характеристических чисел) и вектор произвольных констант. Их скалярное произведение и даст общее решение ДУ.
> w1:=array(1..2,[exp(-t)*cos(sqrt(2)*t),exp(-t)*sin(sqrt);
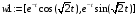
> k1:=array(1..2,[c1,c2]);

> y(t):=evalm(w1.k1);
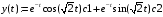
4. Подставим полученное решение в исходное уравнение, используя функцию diff.
> diff(diff(y(t),t),t)+2*diff(y(t),t)+3*y(t)=0; 0=0
> diff(y(t),t,t)+2*diff(y(t),t)+3*y(t)=0; 0=0
В примере показано два способа вычисления второй производной. Функция diff, выполняет дифференцирование (в нашем случае от y(t) по t) для второй и первой производных соответственно.
В окне документов отобразится результат подстановки общего решения в заданное уравнение. Это будет 0 , если решение получено правильно и какая либо функция f(t), если не правильно. Тогда необходимо найти ошибку и повторить вычисления, начиная с того места, где нужно внести исправления.
В примере показано два способа вычисления второй производной. Функция diff, выполняет дифференцирование (в нашем случае от y(t) по t) для второй и первой производных соответственно.
В окне документов отобразится результат подстановки общего решения в заданное уравнение. Это будет 0 , если решение получено правильно и какая либо функция f(t), если не правильно. Тогда необходимо найти ошибку и повторить вычисления, начиная с того места, где нужно внести исправления.
solve(hp,v);
После команды <Enter> (исполнить) получим результат:
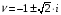
Задача Коши для однородного уравнения
1.Записать,
используя найденное общее решение,
систему алгебраических уравнений для
нахождения неизвестных коэффициентов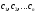 ,
для заданных начальных условий:
,
для заданных начальных условий:
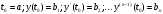 :
:
где
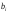 – числа; n
– порядок уравнения.
– числа; n
– порядок уравнения.
2.
Подставить найденные
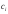 в общее решение и получить решение
задачи Коши для заданных начальных
условий.
в общее решение и получить решение
задачи Коши для заданных начальных
условий.
3. Подставить, для проверки правильности, полученное решение в исходное уравнение.
4. Построить график решения задачи Коши y(t) и на фазовой плоскости в координатах [y(t),y(t)’].
Решение задачи Коши для однородного уравнения в пакете MAPLE
На
предыдущем этапе мы построили общее
решение однородного уравнения с точностью
до неопределённых коэффициентов
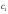 и
и
 .
Это решение – y(t).
Найдем конкретные значения
.
Это решение – y(t).
Найдем конкретные значения
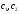 для следующих начальных условий:
для следующих начальных условий:

Рассмотрим последовательность действий и набор функций
MAPLE, необходимых для выполнения пунктов 1-4 раздела 2.
Запишем и построчно введем систему алгебраических уравнений, а затем, используя стандартные функции пакета, решим задачу Коши .
> y(t)=1;
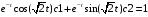
> diff(y(t),t)=2;
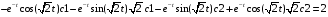
> subs(t=0,exp(-t)*cos(2^(1/2)*t)*c1+exp(-t)*sin(2^(1/2)*t)*c2 = 1);

> subs(t=0,-exp(-t)*cos(2^(1/2)*t)*c1-exp(-t)*sin(2^(1/2)*t)*2^(1/2)*c1-exp(-t)*sin(2^(1/2)*t)*c2+exp(-t)*cos(2^(1/2)*t)*2^(1/2)*c2 = 2);
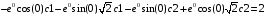
> simplify(%);
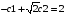
>
simplify(exp(0)*cos(0)*c1+exp(0)*sin(0)*c2 = 1);
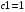
> solve({exp(0)*cos(0)*c1+exp(0)*sin(0)*c2 = 1,-exp(0)*cos(0)*c1-exp(0)*sin(0)*2^(1/2)*c1-exp(0)*sin(0)*c2+exp(0)*cos(0)*2^(1/2)*c2 = 2},{c1,c2});

> evalf(%);
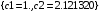
> subs(c1=1,c2=2.1213,y(t));
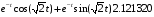
Для построения фазовой траектории, вычислим производную от частного решения.
> y1(t):=exp(-t)*cos(sqrt(2)*t)+2.1213*exp(-t)*sin(sqrt(2)*t);

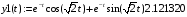
> y2(t):=diff(y1(t),t);
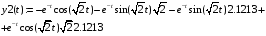
Теперь, используя команду plot, построим графики.
plot(y1(t),t=-1..5); plot([y1(t),y2(t),t=-1..5]);

Рис.1. График y1(t)
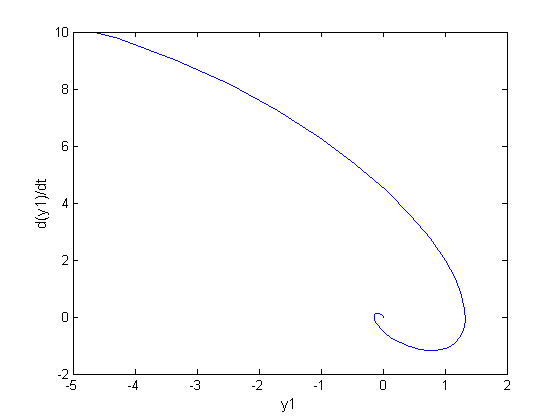
Рис.2. Фазовая траектория
Индивидуальные задания
Построить общее
решение однородного дифференциального
уравнения. Решить задачу Коши. Построить
графики
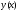 ;
;
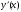 .
Построить фазовую траекторию на плоскости
.
Построить фазовую траекторию на плоскости
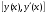 .
.
1. 
2. 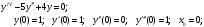
3. 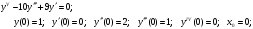
4.
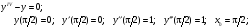
8. 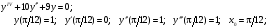
9. 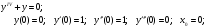
10. 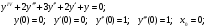
11. 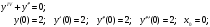
12. 
13. 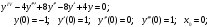
14. 
15. 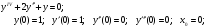
16. 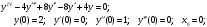
17. 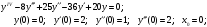
18. 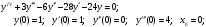
19. 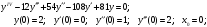
20. 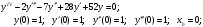
21. 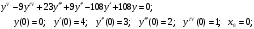
Изучение методов решения однородных дифференциальных уравнений с постоянными коэффициентами порядка N в пакете MAPLE
Методические указания
по выполнению лабораторной работы
Составил:
Козловских Александр Владимирович
Подписано к печати
Формат 60х84.16. Бумага ксероксная.
Плоская печать. Усл. печ.л.. Уч.-изд. л
Тираж зкз. Заказ . Цена свободная.
ИПФ ТПУ. Лицензия ЛТ №1 от 18.07.2011.
Типография ТПУ. 634034, Томск, пр. Ленина, 30.
