
- •Приближённые алгоритмы вычисления характеристик матриц парных сравнений.
- •Характерные особенности деятельности консультативных фирм.
- •Некоторые методы работы консультативных фирм. Организация и проведение конференций по принятию решений.
- •Метод модерации.
- •Основные понятия
- •Обоснование метода Нулевая итерация
- •К-я итерация
- •Алгоритм
- •Формализация
Основные понятия
Определим терминологию:
Пусть
![]() .
.
Введём
на
![]() целевую
функцию
целевую
функцию![]() .
.
Вектора![]() называютсясопряжёнными, если:
называютсясопряжёнными, если: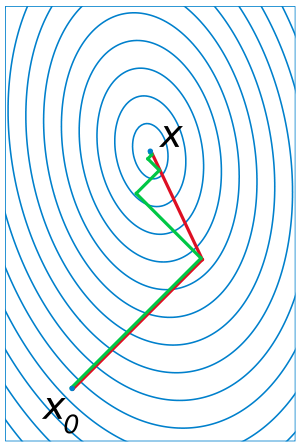
где
![]() —матрица
Гессе
—матрица
Гессе![]() .
.
|
|
Теорема (о
существовании).
Существует
хотя бы одна система
|
|
Обоснование метода Нулевая итерация
Иллюстрация последовательных приближений метода наискорейшего спуска (зелёная ломаная) и метода сопряжённых градиентов (красная ломаная) к точке экстремума.
Пусть
![]()
Тогда
![]() .
.
Определим
направление
![]() так,
чтобы оно было сопряжено с
так,
чтобы оно было сопряжено с![]() :
:
![]()
Разложим
![]() в
окрестности
в
окрестности![]() и
подставим
и
подставим![]() :
:
![]()
Транспонируем
полученное выражение и домножаем на
![]() справа:
справа:
![]()
В
силу непрерывностивторыхчастных
производных![]() .
Тогда:
.
Тогда:
![]()
Подставим полученное выражение в (3):
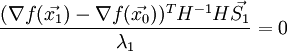
Тогда, воспользовавшись (1) и (2):
![]()
Если
![]() ,
тоградиентв точке
,
тоградиентв точке![]() перпендикуляренградиентув точке
перпендикуляренградиентув точке![]() ,
тогда по правиламскалярного
произведения векторов:
,
тогда по правиламскалярного
произведения векторов:
![]()
Приняв
во внимание последнее, получим из
выражения (4) окончательную формулу для
вычисления
![]() :
:
![]()
К-я итерация
На
k-й итерации имеем набор![]() .
.
Тогда следующее направление вычисляется по формуле:
![]()
где
![]() непосредственно
рассчитывается на k-й итерации, а все
остальные уже были рассчитаны на
предыдущих.
непосредственно
рассчитывается на k-й итерации, а все
остальные уже были рассчитаны на
предыдущих.
Это выражение может быть переписано в более удобном итеративном виде:
![]()
Алгоритм
Пусть
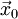 —
начальная точка,
—
начальная точка,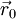 —
направление антиградиента и мы пытаемся
найтиминимумфункции
—
направление антиградиента и мы пытаемся
найтиминимумфункции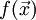 .
Положим
.
Положим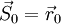 и
найдем минимум вдоль направления
и
найдем минимум вдоль направления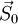 .
Обозначим точку минимума
.
Обозначим точку минимума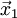 .
.
Пусть на некотором шаге мы находимся в точке
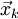 ,
и
,
и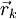 —
направление антиградиента. Положим
—
направление антиградиента. Положим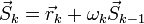 ,
где
,
где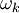 выбирают
либо
выбирают
либо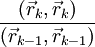 (стандартный
алгоритм), либо
(стандартный
алгоритм), либо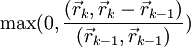 (алгоритм
Полака–Райбера). После чего
найдемминимумв направлении
(алгоритм
Полака–Райбера). После чего
найдемминимумв направлении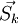 и
обозначим точку минимума
и
обозначим точку минимума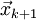 .
Если в вычисленном направлении функция
не уменьшается, то нужно забыть предыдущее
направление, положив
.
Если в вычисленном направлении функция
не уменьшается, то нужно забыть предыдущее
направление, положив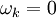 и
повторив шаг.
и
повторив шаг.
Формализация
Задаются начальным приближением и погрешностью:
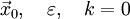
Рассчитывают начальное направление:
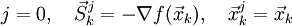
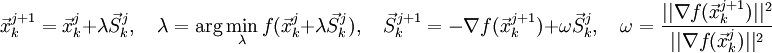
Если
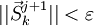 или
или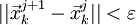 ,
то
,
то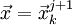 и
останов.
и
останов.Иначе
если
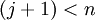 ,
то
,
то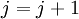 и
переход к 3;
и
переход к 3;иначе
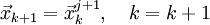 и
переход к 2.
и
переход к 2.
|
Методы оптимизации | |
|
Одномерные |
Метод золотого сечения•Метод деления пополам•Метод дихотомии•Метод парабол•Метод равномерного поиска (перебора)•Метод равномерного блочного поиска•Метод троичного поиска |
|
Прямые методы |
Метод Гаусса•Метод Нелдера — Мида•Метод конфигураций•Метод Розенброка•Метод сопряжённых направлений•Метод Хука — Дживса |
|
Первого порядка |
Градиентный спуск•Метод покоординатного спуска•Метод сопряжённых градиентов |
|
Второго порядка |
Метод Ньютона•Метод Ньютона-Рафсона |
|
Стохастические |
Дифференциальная эволюция•Имитация отжига |
|
Методы линейного программирования |
Метод эллипсоидов•Симплекс-метод•Метод потенциалов |
