
- •З.А. Наседкина, а.В. Песков, а.В. Шитиков сопротивление материалов
- •Оглавление
- •Введение
- •Глава 1. Метод расчета на прочность по допускаемым напряжениям
- •1.1. Внутренние усилия в поперечных сечениях стержня
- •1.2. Понятие о напряжении
- •1.3. Условие прочности по допускаемым напряжениям
- •Вопросы для самоконтроля
- •Глава 2. Растяжение и сжатие
- •Пример 1
- •Задача 1. Растяжение и сжатие (статически определимая система)
- •Статически неопределимые системы
- •Пример 2
- •Задача 2. Растяжение и сжатие (статически неопределимая система)
- •Вопросы для самоконтроля
- •Глава 3. Напряженное и деформированное состояние в точке
- •Пример 3
- •Задача 3. Плоское напряженное состояние
- •Вопросы для самоконтроля
- •Глава 4. Кручение
- •Пример 4
- •Задача 4. Кручение стержней с круглым сечением
- •Вопросы для самоконтроля
- •Глава 5. Моменты инерции плоских сечений
- •Пример 5
- •Задача 5. Моменты инерции плоских сечений
- •Вопросы для самоконтроля
- •Глава 6. Плоский изгиб
- •6.1. Расчет на прочность
- •6.1.1. Построение эпюр внутренних сил Qy и Mz
- •Пример 6
- •6.1.2. Построение эпюр внутренних сил Qy и Mz без записи их уравнений
- •Задача 6. Плоский изгиб (консольная балка)
- •Задача 7. Плоский изгиб (двухопорная балка)
- •Определение перемещений при плоском изгибе
- •Пример 7
- •Задача 8. Определение перемещений при плоском изгибе
- •Вопросы для самоконтроля
- •Глава 7. Расчет на прочность статически неопределимой балки
- •Пример 8
- •Задача 9. Расчет статически неопределимой балки
- •Вопросы для самоконтроля
- •Глава 8. Сложное сопротивление. Кручение и изгиб
- •8.1. Основные понятия
- •Мощность при вращательном движении
- •Пример 9
- •Задача 10. Сложное сопротивление. Кручение и изгиб
- •Вопросы для самоконтроля
- •Глава 9. Устойчивость сжатых стержней
- •Пример 10
- •Пример 11
- •Задача 11. Устойчивость сжатых стержней
- •Вопросы для самоконтроля
- •Глава 10. Динамическое действие нагрузок
- •Пример 12
- •Задача 12. Динамическое действие нагрузок
- •Вопросы для самоконтроля
- •Библиографический список
- •Указания по выполнению контрольных работ
- •Перечень контрольных заданий (номера и названия задач)
- •Геометрические характеристики поперечных сечений
- •Сортамент прокатной стали Сталь горячекатаная. Балки двутавровые (гост 8239 – 72)
- •Сталь горячекатаная. Швеллсры (гост 8240-72)
- •Сталь прокатная угловая неравнополочная (гост 8510 – 72)
Пример 3
Исследовать плоское напряженное состояние стального кубика
(рис. 10, а).

Рис. 10. Hормальные и касательные напряжения по граням кубика:
а – направления напряжений для исследуемого напряженного состояния;
б – положительные направления напряжений
Абсолютные величины напряжений (см. рис. 10, а):
σx = 100 МПа; σy = 70 МПа; τxy = τyx = 50 МПа; Е = 2 ·105 МПа; μ = 0,25.
Прежде всего установим знаки нормальных и касательных напряжений, показанных на рис. 10, а. Положительные направления
нормальных напряжений σx, σy и касательных напряжений τxy = τyx показаны на рис. 10, б. Нормальные растягивающие напряжения принято брать со знаком плюс, а сжимающие – со знаком минус. Следовательно, σx = –100 МПа и σy = 70 МПа, τxy= –50 МПа.
Определение главных напряжений. Наибольшее σ1:
![]()
![]()
наименьшее из главных напряжений σ2 :

![]()
![]()
Определение направления главных площадок. Угол наклона нормали главной площадки к оси X определяется по формуле
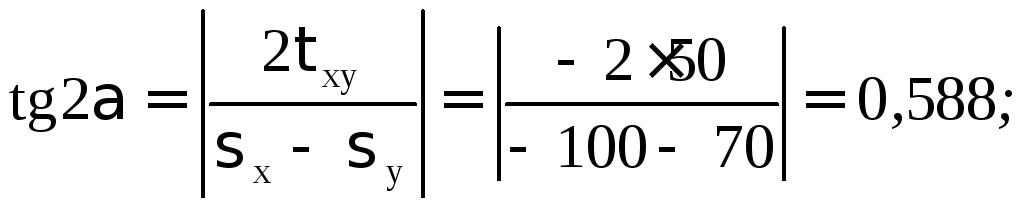
![]()
![]()
Знак касательных напряжений и угла α можно не устанавливать, если пользоваться следующим правилом для определения ориентации главных площадок.
Главные площадки, на которых действует наибольшее из главных напряжений σ1, получаются поворотом на угол α тех из исходных площадок, на которых действует большее (по алгебраической величине) из исходных напряжений σx, σy. В нашем примере такими исходными площадками будут площадки, где действует нормальное напряжение σy, так как σy > σx.
Направление поворота указывает стрелка касательного напряжения на исходной площадке (рис. 11). Вторая пара главных площадок перпендикулярна найденным.
Определение максимальных касательных напряжений:
![]() МПа.
МПа.
Эти напряжения действуют на площадках, наклоненных под углом 45° к главным, и направлены в сторону σ1 (см. рис. 11).
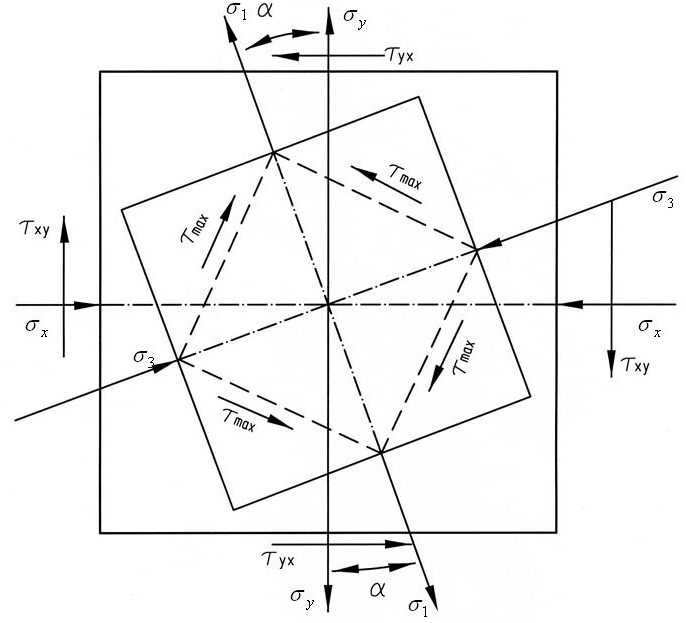
Рис. 11. Расположение главных площадок
Определение относительных деформаций εx, εy, εz:
![]()
![]()
![]()
![]()
Обратите внимание на то, что при σz = 0 εz ≠ 0 , т.е. при отсутствии напряжения по оси Z деформация в этом направлении имеет место.
Определение относительного изменения объема θ:
![]() .
.
Определение удельной потенциальной энергии деформаций. Потен- циальная энергия изменения объема Uоб:
Uоб
![]() МПа.
МПа.
Потенциальная энергия изменения формы Uф:
Uф

![]() МПа
(Н/мм2).
МПа
(Н/мм2).
Полная энергия U:
U = Uоб + Uф = 46·10–3 = 46·10–3 МПа (Н/мм2).
Задача 3. Плоское напряженное состояние
Исследовать плоское напряженное состояние (рис. 12). Данные к задаче приведены в табл. 3.
План решения задачи:
1) найти главные напряжения и направления главных площадок;
2) вычислить максимальные касательные напряжения;
3) определить относительные деформации;
4) найти относительное изменение объема;
5) найти удельную потенциальную энергию деформаций.
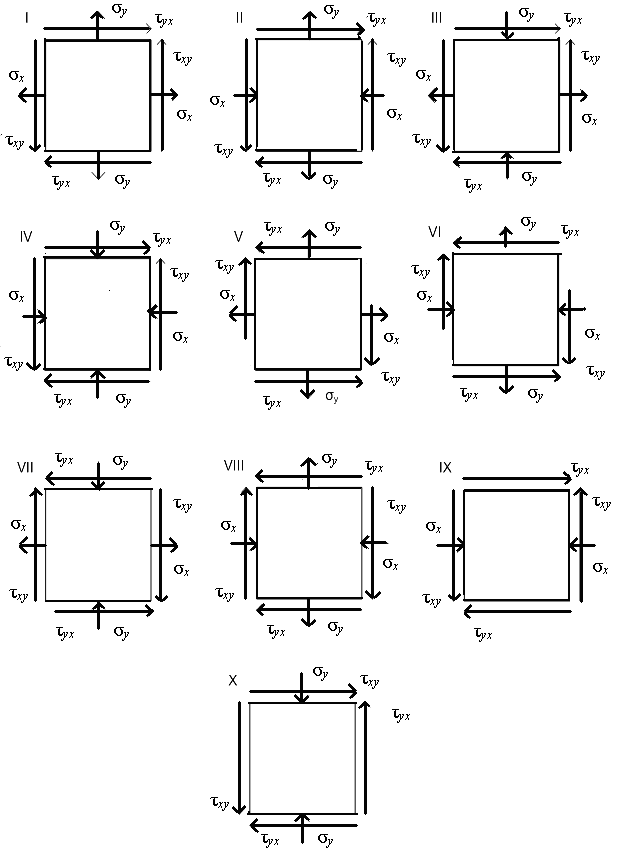
Рис. 12. Схемы к задаче 3
Таблица 3
Данные к задаче 3
|
Номер строки |
Номер схемы |
σх, МПа |
σy, МПа |
τxy, МПа |
|
1 |
I |
10 |
10 |
10 |
|
2 |
II |
20 |
20 |
20 |
|
3 |
III |
30 |
30 |
30 |
|
4 |
IV |
40 |
40 |
40 |
|
5 |
V |
50 |
50 |
50 |
|
6 |
VI |
60 |
60 |
60 |
|
7 |
VII |
70 |
70 |
70 |
|
8 |
VIII |
80 |
80 |
80 |
|
9 |
IX |
90 |
90 |
90 |
|
0 |
X |
100 |
100 |
100 |
|
|
в |
а |
б |
в |
