MATLAB_Lab_all / Лабораторная работа 3 mathlab

Лабораторная работа №3

Решение эллиптических уравнений

Эллиптические уравнения возникают во многих задачах физики и техники: исследование прогиба нагруженной мембраны, давления газа в неоднородном силовом поле, стационарного распределения тепла или электрического потенциала и т.п. В этих задачах предполагается, что внешние воздействия не зависят от времени, а начальные условия были заданы достаточно давно, так что система успела подстроиться к ним и перейти в стационарный режим. Типичным случаем является задача Дирихле с уравнением Пуассона и краевыми условиями первого рода. На её примере и рассмотрим особенности численного решения эллиптических уравнений.

Пусть в квадратной области 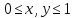необходимо найти функцию 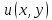, удовлетворяющую уравнению Пуассона:

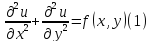
и граничным условиям общего вида:

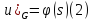
где G – граница области (граница квадрата), s – длина дуги вдоль границы G (определеямая х или y координатами вдоль соответствующей части границы), f и φ –заданные функции.

Запишем конечно-разностный аналог уравнения (1). Для этого введём на рассматриваемой области равномерную сетку с N+1 узлами (x_i, y_j) = (ih, jh) и шагом h = 1/N. Тогда после замены производных в (1) на их трёхточечную аппроксимацию получим:

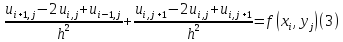
Несложно видеть, что (2) представляет собой систему линейных алгебраических уравнений относительно u_i,j. Решать эту систему общими методами линейной алгебры (например, Гаусса) невыгодно, поскольку они, как правило, не учитывают сильную разреженность матрицы системы. Вместо этого используют специальные методы как прямые, так и итерационные. Итерационные методы обычно не обладают высокой скоростью, зато более универсальны, не зависят от геометрии расчётной области и легче программируются. Далее рассмотрим один из простейших итерационных методов решения эллиптических уравнений – счёт на установление.

Рассмотрим вспомогательную нестационарную задачу с теми же граничными условиями (2), но с уравнением параболического типа (уравнение теплопроводности):

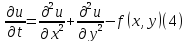
и с произвольным начальным условием , также удовлетворяющим граничным условиям (2). Можно показать, что решение данной задачи в пределе 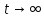стремится к решению исходного уравнения (1) с граничными условиями (2). Поэтому далее будем решать нестационарную задачу до установления, для чего перепишем разностную схему (3) в соответствии с новой постановкой в виде:

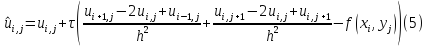
где была использована конечно разностная аппроксимация производной по времени и введён «временной шаг» τ. Такая схема называется явной, поскольку с её помощью мы имеем возможность непосредственно по известным значениям 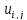находить неизвестные 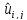на следующем «временном слое». При этом устойчивый счёт по явной схеме возможен при условии:

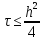
Итерации продолжаются, пока невязка задачи (1) не окажется меньше наперёд заданного числа ε<1. Отметим, что сходимость итераций по схеме (5) имеет место и в случае расчётной области произвольной формы. Кроме того, схему (4-5) можно обобщить и на случай задачи Дирихле с переменными коэффициентами, что позволяет решать задачи, заданные в криволинейных системах координат.

Задание

1. Решить численно эллиптические уравнения используя счёт на установление:

1. , ,

2. , ,

3. , ,

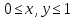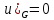
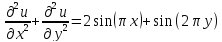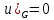
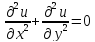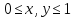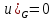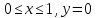
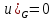при

при

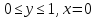
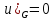при

при

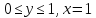
Принять ε=10^-4.

2. Оптимизировать вычисления в циклах, используя индексацию массивами, и сравнить выигрыш по времени.

3. В процессе решения на каждой десятой итерации построить графики приближений решения уравнения и локальной невязки, используя графические возможности MatLab.