MATLAB_Lab_all / Лабораторная работа 1 matlab

Лабораторная работа №1

Простейшие вычисления и использование одномерных массивов

1. Работа с данными в командной строке MatLab

При работе в MatLab нет необходимости определять тип и размерность переменных. Когда MatLab находит выражение, инициализирующее переменную, он автоматически выделяет в памяти нужный объѐм для хранения переменой или изменяет (увеличивает или уменьшает), если переменная до этого уже существовала. Например, команда

>> x = 12345

создаст х как матрицу 1х1 (т.е. скаляр) с единственным элементом, в который будет помещено значение 12345. Имена переменных в MatLab могут быть заданы последовательностью букв, цифр или символов подчѐркивания, причѐм допустимы оба регистра букв, т.к. MatLab различает заглавные и строчные буквы.

При явной инициализации переменных числами в MatLab используется общепринятая десятичная система счисления с десятичной точкой и знаками + и –. Числовые значения переменных хранятся в памяти в стандартном формате long и используются при вычислениях с двойной точностью float64, которой соответствует тип double из С\С++.

В системе MatLab имеется несколько предопределенных констант, которые принято называть системными переменными, поскольку, с одной стороны, они задаются системой при загрузке, а с другой — могут быть переопределены:

i или j — мнимая единица

pi — число пи

eps — погрешность операций с плавающей точкой (2^-52)

realmin — наименьшее число с плавающей точкой (2^-1022)

realmax — наибольшее число с плавающей точкой (2^1023)

inf — эквивалент бесконечности

ans — переменная, по умолчанию хранящая результат последней операции в командной строке

NaN — результат некорректных операций (Not a number).

Например, комплексное число (2.3, 5.4) можно определить так

>> z = 2.3 + 5.4i.

Выражения, содержащие только скалярные переменные 1х1, используют обычные арифметические операции и стандартный приоритет действий над числами, изменяемый с помощью скобок (): + - сложение, – - вычитание, * - умножение, / - деление, ^ - возведение в степень.

Массивы, как и скалярные данные, в MatLab не требуют особых способов описания при создании, достаточно присвоить какой-либо переменной значение в виде массива. В MatLab двумерные массивы принято называть матрицами, а одномерные массивы (1 х n) – строками (англ. row), а (n x 1) – векторами. Массивы можно инициализировать явно, используя для этой цели группирующие скобки []. Например, команда:

>> a = [-1 5 2 -3 10]

создаст массив с элементами -1, 5, 2, -3, 10. Доступ к элементам массива производится с помощью индексной ссылки на элемент – a(i). Наименьшее значение индекса элемента массива в MatLab равно 1. Таким образом, в предыдущем примере:

a(1) = -1, a(2) = 5, a(3) = -2, a(4) = -3, a(5) = 10.

При попытке обратиться к элементам a(0) или a(6) система выведет сообщение об ошибке,

т.к. индекс элемента массива должен быть положительным целым числом или результатом логического выражения и не должен выходить за пределы массива.

Создать одномерный массив-вектор можно, используя операцию транспонирования «’» (символ одиночная кавычка) из массива-строки:

b = a’

или с помощью операции объединения, используя группирующие скобки [] и разделитель «;» (символ точка с запятой)

с = [6; -1; 7; 8; 0].

Строго говоря, индексировать массивы-строки и векторы необходимо парой индексов как двумерный массив, т.е. для массива-строки должно быть – а(1, 1), а(1, 2), а(1, 3) и т.д., а для вектора – с(1, 1), с(2, 1), с(3, 1) и т.д. Однако на практике допустимо использовать обычную индексацию по основному измерению массива, опуская второй индекс – а(1), а(2), а(3) и т.д. Это удобно, но в некоторых случаях (например, при попытке сложить строку и вектор) может привести к ошибкам, т.к. при совершении бинарных операций необходимо, чтобы размеры и размерности массивов были согласованы. Т.е.

операция с массивами из предыдущих примеров a + c приведѐт к ошибке, тогда как выражения a’ + c и b + c допустимы.

Итак, в MatLab можно производить математические действия над массивами, как над обычными переменными, в обход привычных для других языков программирования циклических конструкций. На практике это означает, что код программы становится проще и компактнее, но главное в том, что математические операции над массивами оптимизированы и выполняются ощутимо быстрее в сравнении с их аналогами, написанными через циклы.

Для основных операций действуют простые и очевидные соглашения. При сложении и вычитании массивов их размеры и размерности должны быть согласованы, т.е. для вычисления a+b и a-b необходимо, чтобы a и b имели одинаковые размеры (n x m х p x q x …). Для операций умножения, деления и возведения в степень соглашения

несколько иные. Возможны поэлементные операции, когда, скажем, элементы первого массива умножаются на элементы второго, т.е.:

c(i, j) = a (i, j) * b(i, j).

В этом случае бинарная операция «умножить массивы» записывается через оператор «.*»

c = a.*b.

Аналогично определены операции «./» и «.^». Для поэлементных операций, как и для операций сложения и вычитания, необходимо, чтобы массивы a и b имели одинаковые размеры по всем измерениям.

Возможны и операции «*», «/» и «^». Однако в отличие от поэлементных операций они производятся по правилам линейной алгебры над двумерными матрицами, а также строками и векторами. Например, допустима операция а*b, если a имеет размеры (n x m), а b размеры (m х p). В частности, если а – строка, а b – вектор одинаковой длины, то в результате операции а*b будет получено их скалярное произведение.

MatLab предоставляет в распоряжение пользователя большое количество стандартных элементарных математических функций, таких как sqrt, abs, exp, sin, tanh и др. Имеются и более специфические функции, например, функции Бесселя и гаммафункция. Замечательно то, что функции математической библиотеки MatLab без ограничений применимы к массивам и комплексным данным. Необходимо только помнить, что выполняются они поэлементно, т.е. полученная в результате расчѐта матрица с=sin(a) будет содержать элементы с(i, j) = sin(a(i, j)).

В заключении обзора приведѐм ещѐ несколько полезных функций, упрощающих работу с массивами:

mean(a) - вычисляет среднее арифметическое элементов массива а

std(a) - вычисляет среднеквадратичное отклонение элементов массива а

sum(a) - вычисляет сумму элементов массива а

diff(a) – вычисляет разность между элементами соседних строк массива а

prod(a) - вычисляет произведение элементов массива а

min(a) - вычисляет минимум элементов массива а

max(a) - вычисляет максимум элементов массива а

sort(a) - сортирует элементы а по возрастанию.

Важно помнить, что если массив-аргумент – двух- и более мерный, то эти операции по умолчанию производятся по столбцам (второму измерению) массива-аргумента. Например, результатом операции mean(А) над двумерным массивом А будет массивстрока, элементы которой равны среднему арифметическому элементов А в соответствующем столбце. Отметим также, что полученный в результате выполнения команды diff(А) массив будет иметь на одну строку меньше в сравнении с А (в том числе, если А – одномерный массив; даже в этом случае он будет содержать на один элемент меньше).

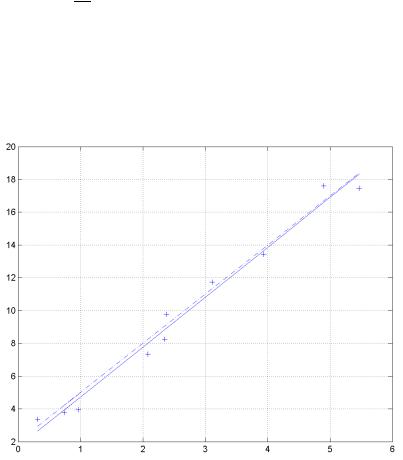
Качественно оценить результаты расчѐтов можно и графически (см. рис. 1). Как видно из рисунка, отклонение графика аппроксимирующей зависимости от точной визуально весьма невелико, а «экспериментальные» точки равномерно расположены относительно неѐ.

Рис. 1. Результаты обработки данных методом наименьших квадратов. Крестиками показаны «экспериментальные» данные, полученные добавлением случайных отклонений к точным значениям линейной функции, показанной пунктиром. Сплошная линия – график зависимости, полученной методом наименьших квадратов.

Задания

С помощью метода наименьших квадратов найти параметры зависимости y = a + bx по известным «экспериментальным» данным, определить их погрешность и сравнить с точными значениями (см. формулы 3-5):

1.х = 0 0.1000 0.2000 0.5000 0.9000 1.5000 2.9000 3.0000 3.3000 3.7000;

y = 4.7060 4.3318 4.8769 5.5462 6.7971 9.3235 13.3948 13.3171 14.8502 15.1344;

Точные значения: а = 4, b = 3.

2.х = -1.3200 -0.5000 -0.3500 -0.3000 -0.1300 0.5600 0.8000 1.0000 1.1500 1.3300; y = 9.3513 4.7551 4.2560 4.1991 3.5409 0.1593 -1.4528 -2.8614 -3.6007 -4.3925;

Точные значения: а = 2, b = -5.

3.х = 1.7800 1.9700 2.0000 2.0100 2.3900 2.8900 3.4600 4.2500 4.3600 4.7100; y = 0.4117 1.2708 1.0853 1.0697 2.1972 2.5658 4.1772 5.7537 5.6004 6.4878;

Точные значения: а = -3, b = 2.

4.х = -2.9100 -2.5700 -2.4000 -1.9700 -0.3100 0.7500 1.2400 1.5500 3.2300 4.4700; y = 9.0333 10.0638 7.8093 8.4898 5.2546 3.2374 0.6889 0.6996 -2.9403 -4.3399;

Точные значения: а = 4, b = -2.

5.х = -2.6600 -2.2300 -0.6400 -0.4200 -0.0800 0.4200 0.4300 3.3000 3.3100 3.6100;

y = -12.4195 -11.9105 -7.4366 -6.4522 -6.0471 -4.4761 -2.8259 5.8123 5.0804 4.9496;

Точные значения: а = -5, b = 3.

6.х = -4.8500 -4.5700 -3.3200 -2.6600 -1.4700 -0.5000 1.4700 1.4900 2.3100 3.2100; y = 6.9440 6.1626 5.8094 4.0379 3.8436 1.8670 0.2670 0.7612 0.2505 -2.0477;

Точные значения: а = 2, b = -1.

7.х = 2.1400 3.0500 3.1200 3.4000 3.5500 3.5700 5.4200 5.5600 5.7200 6.5000;

y = 12.9886 17.0072 18.2232 19.0657 19.4515 20.7280 29.8519 29.9003 30.8450 34.6741;

Точные значения: а = 2, b = 5.

8.х = -1.8100 -1.6400 -1.5500 -1.4200 -1.4100 -1.3900 -0.9000 0.0400 0.2900 2.9100; y = 8.0522 8.7668 7.5104 6.6296 8.0398 8.1295 5.5777 2.1022 1.6461 -5.9126;

Точные значения: а = 3, b = -3.

9.х = -1.1800 -0.4500 -0.1700 0.0700 0.2300 0.9600 1.5500 2.1600 2.2100 2.9700;

y = 3.0710 -0.2250 -0.5480 -3.2916 -2.2923 -6.3393 -9.7728 -12.6429 -13.5754 - 16.9323;

Точные значения: а = -2, b = -5.

10.х = -0.8500 -0.1700 -0.0300 0.4400 0.6000 0.7300 1.1200 1.3900 2.8100 2.9300;

y = -8.3245 -3.9097 -3.2934 -1.6476 -2.4026 -1.5563 0.1507 1.9195 6.5131 8.1625;

Точные значения: а = -4, b = -4.