
матан
.pdf
§9. Обобщения понятия предела функции |
81 |
||||||
|
|
|
|
0 |
|
|
|
|
− |
|
ε |
ε |
|||
ОПРЕДЕЛЕНИЕ 9.1. Пусть E R – произвольное множество. Будем говорить, что +∞ (−∞) является предельной точкой множества E, если в любой ε-окрестности +∞ (−∞) имеется хотя бы одна точка множества E, другими словами, когда множество E не ограничено сверху (снизу).
ОПРЕДЕЛЕНИЕ 9.2. Пусть E R – произвольное множество, имеющее +∞ в качестве предельной точки. Будем говорить, что функция y = f(x), заданная на E, имеет пре-
делом A R при x → +∞, если для всякой ε-окрестности A найдется δ(ε)-окрестность +∞ такая, что при изменении x в δ(ε)-окрестности +∞ значения f(x) лежат в ε-окрестности A.
Запишем определения некоторых пределов:
1. |
x |
lim |
f(x) = A |
, |
A |
|
R |
: |
|
|
|
+ |
∞ |
|
|
|
|
|
|||||
|
|
→ |
δ(ε) : x > δ(ε) выполнено |f(x)−A| < ε. |
||||||||
ε > 0 |
|||||||||||
2. |
x |
lim |
f(x) = + |
|
|
|
|
|
|
||
+ |
∞ |
|
∞: |
|
|
|
|
|
|||
|
|
→ |
|
|
|
|
|
|
выполнено |
|
|
3. |
ε > 0 δ(ε) : |
|
x > δ(ε) |
f(x) > ε. |
|||||||
x |
lim |
f x |
|
|
|
|
|
|
|
||
+ |
∞ |
( ) = −∞: |
|
|
|
|
|
||||
|
|
→ |
|
|
|
|
|
|
выполнено |
|
|
|
ε > 0 δ(ε) : |
x > δ(ε) |
f(x) < −ε. |
||||||||
4. |
xlim |
f(x) = +∞: |
|
|
|
|
|
||||
|
|
→−∞ |
δ(ε) < 0 : x < δ(ε) выполнено f(x) > ε. |
||||||||
ε > 0 |
|||||||||||
5. |
xlim0 f(x) = −∞: |
|
|
|
|
|
|||||
|
|
→− |
|
|
|
|
|
|
|
|
|
ε > 0 δ(ε) < 0 |
: x, δ(ε) < x < 0 выполнено f(x) < −ε. |
||||||
6. |
x |
lim |
f x |
|
a > |
0: |
|
→ |
a+0 |
( ) = +∞, |
|
||||
|
|
|
|
: x, a < x < a+δ(ε) выполнено f(x) > ε. |
|||
ε > 0 δ(ε) > 0 |
|||||||
7. |
|
lim |
f(x) = +∞: |
|
|
||
|
x→a+0 |
|
|
|
|
||
ε > 0 : δ > 0 x : a < x < a+δ, для которого f(x) < ε.
УПРАЖНЕНИЕ 1. Сформулировать и доказать критерий Коши существования пределов f(x) → ±∞ при x → ±∞.

82 |
Глава 3. Непрерывные функции и их свойства |
§10. Асимптоты
Пусть f – функция, определенная на интервале (a, +∞) (или (−∞, a)). Предположим, что при x → +∞ (−∞) выполнено
x + ( ) |
[f(x) |
− |
(A x + B)] = 0. |
(1) |
lim |
|
|
→ ∞ −∞
Прямая y = A x + B называется в этом случае асимптотой функции f при x → +∞ ( −∞).
Если lim f(x) = ±∞, то в данном случае говорят,
x→c+0 ( c−0)
что f имеет в точке x = c вертикальную асимптоту справа
(слева).
ТЕОРЕМА 10.1. Условие (1) эквивалентно паре условий
|
lim |
|
|
|
f(x) |
|
= A, |
|
|
|
|
|
|
||||
|
|
|
|
|
|
|||
+ |
( |
|
) |
|
|
− |
|
|
x |
|
|
x |
|
||||
x→+∞ |
( |
−∞) |
|
|
|
|||
|
|
|
|
|
|
|
|
(2) |
|
lim |
|
|
(f(x) A x) = B. |
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
→ ∞ |
|
−∞ |
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
Доказательство. Докажем, что соотношение (1) влечет (2). Ясно, что из (1) следует
Однако
lim
x→+∞( −∞)
и потому
|
|
lim |
) |
(f(x) |
− |
A x) = B. |
|
|
|
|
|
|
|||||||
|
x |
→ |
∞ |
−∞ |
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
+ |
( |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
(f(x) |
− |
(A x + B)) = |
|
|
lim x |
|
f(x) |
|
A |
B |
, |
||||||||
|
|
|
|
|
|
||||||||||||||
|
|
x |
− |
− x |
|||||||||||||||
|
|
|
|
|
|
x→+∞( −∞) |
|
|
|||||||||||
|
|
lim |
|
f(x) |
|
A |
|
. |
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
x − |
= 0 |
|
|
|
|
|
|
|||||||||
|
x→+∞( −∞) |
|
|
|
|
|
|
|
|
||||||||||
Обратно, (2) влечет (1). Это также ясно, поскольку (1) непосредственно вытекает из второго соотношения в (2).
ПРИМЕР 1. Найдем асимптоты функции
y = 2x + x1 + 1.
Во-первых, понятно, что функция имеет вертикальную асимптоту в точке x = 0 слева и справа.
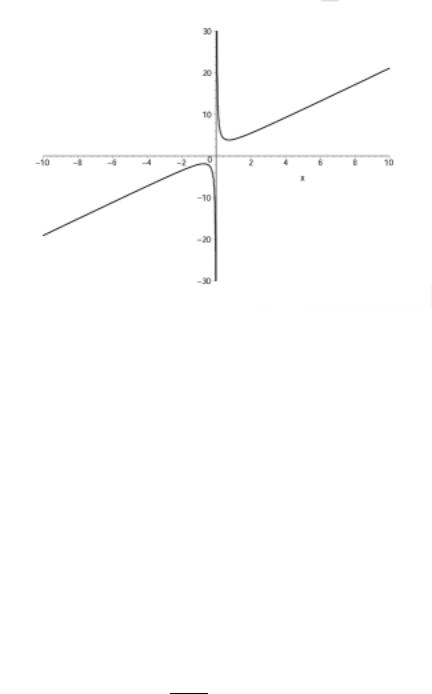
§11. Асимптотические формулы |
83 |
Во-вторых, заметим, что |
|
|
|
|
|
|
|||||
lim |
y(x) |
= lim (2 + |
1 |
+ |
|
1 |
) = 2 . |
||||
|
x2 |
|
|||||||||
x→±∞ |
x |
|
|
x→±∞ |
|
|
x |
||||
Далее находим |
|
|
|
|
|
|
|
|
|
|
|
lim (y(x) |
|
|
2x) = lim |
|
1 |
+ 1 = 1 . |
|||||
− |
x |
||||||||||
x→±∞ |
|
x→±∞ |
|
|
|
|
|||||
Таким образом, функция имеет при x → ±∞ асимптоту y = 2x + 1.
§11. Асимптотические формулы. Классификация бесконечно малых
Пусть y = f(x) и y = g(x) = 0 – функции с общей областью определения, имеющей точку a в качестве точки сгущения.
ОПРЕДЕЛЕНИЕ 11.1. Говорят, что f(x) и g(x) функции одного порядка при x → a, и пишут
f(x) = O(g(x)) (x → a),
если существует постоянная M > 0 : x = a и достаточно близких к a выполнено
−M < f(x) < M. g(x)

84 Глава 3. Непрерывные функции и их свойства
ПРИМЕР 1. Мы имеем
sin |
1 |
= O(1) (x → 0) |
|||
|
|||||
x |
|||||
и |
|
|
|
||
1 |
|
= O(sin 2x) |
(x → 0). |
||
x sin |
|
|
|||
x |
|||||
УПРАЖНЕНИЕ 1. Поясните, |
что означает запись |
||||
f(x) = O(1). |
|
|
|
||
ОПРЕДЕЛЕНИЕ 11.2. Говорят, что f(x) эквивалентна g(x) при x → a, и пишут
f(x) g(x) (x → a) ,
если
lim f(x) = 1.
x→a g(x)
Отметим некоторые пары эквивалентных функций: 1. sin x x (x → 0).
Доказательство было дано ранее (первый "замечательный" предел).
2. 1 − cos x x22 (x → 0).
Доказательство.
|
|
lim |
1 − cos x |
= lim |
2 sin2 x2 |
|
= lim |
2(x2 )2 |
= 1. |
|||||||
|
|
|
x2/2 |
x2/2 |
||||||||||||
|
|
x→0 |
x2/2 |
x→0 |
|
|
x→0 |
|
||||||||
3. |
tg x x (x → 0). |
|
|
|
|
|
|
|
|
|
|
|||||
Действительно, мы имеем |
|
|
|
|
|
|
||||||||||
|
|
|
|
lim |
tg x |
= lim |
sin x |
|
1 |
|
= 1. |
|
||||
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
x→0 x |
x→0 x |
cos x |
|
|
||||||||
4. |
√ |
|
− 1 nx (x → 0) n = 1, 2, . . .. |
|
||||||||||||
1 + x |
|
|||||||||||||||
|
n |
|
|
|
|
|
|
|
|
|
|
|
|
|
||
Доказательство. Воспользуемся формулой
an − bn = (a − b)(an−1 + an−2b + an−3b2 + . . . + abn−2 + bn−1)
для a = (1 + x)1/n, b = 1. Имеем:
|
n |
|
|
|
|
|
|
|
|
|
lim |
√ |
1 + x − 1 |
= lim |
|
|
(1 + x) − 1 |
|
= 1. |
||
|
x |
x |
|
|
|
|||||
x→0 |
|
x→0 |
n−1 |
|
1 |
|
||||
|
n |
n |
((1 + x) n |
|
+ . . . + (1 + x)n + 1) |
|
||||

§11. Асимптотические формулы |
|
|
|
|
|
|
|
85 |
||||||
5. ex − 1 x (x → 0). |
|
|
x |
− 1 = z. Тогда |
|
|||||||||
Для доказательства положим e |
|
|
||||||||||||
|
|
ex = z + 1 x = ln(1 + z) |
|
|
||||||||||
lim |
ex − 1 |
|
= lim |
|
z |
= lim |
|
1 |
= |
|||||
|
|
|
|
|
|
|||||||||
x→0 |
x |
z→0 ln(1 + z) |
|
z→0 z1 · ln(1 + z) |
|
|||||||||
= lim |
|
1 |
|
= |
|
|
1 |
|
|
= |
|
|
1 |
= 1. |
|
1 |
|
|
|
|
1 |
|
|
1 |
|||||
z→0 ln(1 + z)z |
|
lim ln(1 + z)z |
|
ln lim(1 + z)z |
|
|||||||||
|
|
|
|
z→0 |
|
|
|
|
|
z→0 |
|
|
||
Здесь использована непрерывность функции y = ln x. (В каком именно месте?)
6. |
ln(1 + x) x (x → 0). |
|
|
||
Доказательство. |
|
|
|
||
|
lim |
ln(1 + x) |
1 |
1 |
|
|
|
= lim ln(1 + x)x = ln lim(1 + x)x = 1. |
|
||
|
x |
|
|||
|
x→0 |
x→0 |
x→0 |
|
|
7. |
α = 0 имеем |
|
|
||
|
|
(1 + x)α − 1 αx при |
x → 0. |
(1) |
|
Действительно, |
|
|
|
||
|
|
ln(1 + x)α = α ln(1 + x) αx |
(x → 0) . |
|
|
С другой стороны,
ln(1 + x)α = ln{[(1 + x)α − 1] + 1},
причем |
при |
x → 0. |
[(1 + x)α − 1] → 0 |
||
Однако |
|
|
ln(1 + ε(x)) ε(x) |
при |
ε(x) → 0. |
Значит, |
|
|
ln([(1 + x)α − 1] + 1) (1 + x)α − 1 (x → 0) .
Легко видеть, что отношение эквивалентности транзитивно и
потому
αx (1 + x)α − 1 (x → 0).

86 |
Глава 3. Непрерывные функции и их свойства |
ОПРЕДЕЛЕНИЕ 11.3. Говорят, что функция y = f(x)
является бесконечно малой при x → a, если lim f(x) = 0.
x→a
ОПРЕДЕЛЕНИЕ 11.4. Будем говорить, что y = f(x) есть бесконечно малая по сравнению с y = g(x) при x → a, и писать
f(x) = o(g(x)) (x → a),
если
lim f(x) = 0.
x→a g(x)
ПРИМЕР 2. Функции f(x) = sin2 x и g(x) = x бесконечно малые при x → 0. Справедливо равенство
sin2 x = o(x) (x → 0).
Другими словами, функция sin2 x стремится к нулю быстрее, чем x. 
УПРАЖНЕНИЕ 2. Поясните, что означает запись f(x) = o(1) при x → a.
Все формулы указанного выше вида называются асимптотическими формулами.
ТЕОРЕМА 11.1. Функция y = f(x) имеет пределом в точке a число A тогда и только тогда, когда функция (f(x) − A) является бесконечно малой при x → a.
Доказательство. Пусть lim f(x) = A. Тогда ясно, что
x→a
lim(f(x) − A) = 0. Это означает в свою очередь, что (f(x) −
x→a
A) – бесконечно малая при x → a.
Обратно. Пусть (f(x) − A) – бесконечно малая при x → a.
Тогда lim(f(x) − A) = 0. Отсюда по теореме о пределе раз-
x→a
ности lim f(x) − A = 0.
x→a
Пусть α(x) бесконечно малая при x → a. Если f = o(αn(x)) при x → a, то бесконечно малая f называется бесконечно малой порядка n относительно бесконечно малой α (если f = o(α(x)) при x → a, то говорят, что f является бесконечно малой более высокого порядка, чем α).
В таком случае простейшими бесконечно малыми естественно назвать бесконечно малые вида
C · αK(x), C ≡ const = 0, K > 0.

§11. Асимптотические формулы |
87 |
Говорят, что бесконечно малая β(x) (x → a) имеет порядок K > 0 по сравнению с бесконечно малой α(x), если
|
β(x) CαK(x), |
(x → a). |
(2) |
||||||
Ясно, что это соотношение можно переписать в виде |
|
||||||||
β(x) = C · αK(x) + |
|
|
(αK(x)) (x → a). |
(3) |
|||||
o |
|||||||||
Действительно, (2) означает, что |
|
||||||||
|
β(x) |
|
|
|
|
|
β(x) |
|
|
lim |
|
= 1 |
|
|
|
|
|
= 1 + ε(x) |
|
|
C |
|
|
||||||
x→a C · αK(x) |
|
· αK(x) |
|
||||||
(здесь ε(x) – бесконечно малая при x → a). Таким образом,
β(x) = C · αK(x) + ε(x)[C · αK(x)]
или
β(x) = CαK(x) + o(αK(x)) (x → a).
Иногда, вместо того, чтобы записывать формулу (3), говорят, что CαK(x) является главной частью бесконечно малой β(x) по сравнению с бесконечно малой α(x). Другими словами, выражение "CαK(x) является главной частью бесконечно малой β(x) по сравнению с бесконечно малой α(x)" означает, что бесконечно малые α(x) и β(x) связаны соотношением (3) или, что равносильно, соотношением (2).
ПРИМЕР 3. Предположим, что основная бесконечно малая α(x) при x → 0 есть x. Выделим главные части других бесконечно малых
a) β(x) = 1 −cos(x). Главная часть β(x) равна x22 при x → 0.
б) β(x) = tg x − sin x. Тогда
|
|
|
|
|
|
1 |
|
|
|
|
1 |
|
|||
β(x) = tg x − sin x = sin x( |
|
|
|
|
− 1) x( |
|
− 1) = |
||||||||
cos x |
cos x |
||||||||||||||
|
|
= x |
|
|
1 − cos x |
|
x3 |
, |
(x |
|
0), |
|
|||
|
|
|
|
|
|
|
|
||||||||
|
|
· |
cos x |
2 |
→ |
|
|||||||||
|
|
|
|
|
|
|
|
|
|
||||||
т.е. |
x3 |
– |
главная |
часть |
|
|
бесконечно |
малой |
|||||||
2 |
|
|
|||||||||||||
β(x) = tg x − sin x.

88 |
Глава 3. Непрерывные функции и их свойства |
ПРИМЕР 4. Предположим, что основная бесконечно малая
α(x) = x1 , (x → +∞).
Выделим главную часть бесконечно малой
√ √ √
β(x) = x + 1 + x − 1 − 2 x .
Покажем сначала, что β(x) есть бесконечно малая. Действительно
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
√ |
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
||||||||
β(x) = |
x + 1 + x − 1 + 2 |
x |
− 1 |
− 4x |
= |
|||||||||||||||||||||||
|
|
|||||||||||||||||||||||||||
|
|
|
√ |
|
|
√ |
|
|
|
|
√ |
|
|
|
||||||||||||||
|
|
|
|
|
|
|
x + 1 + x − |
1 + 2 |
|
|
x |
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
√ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
= |
√ |
2( |
x√− 1 − |
x) √ |
|
= |
|
|
||||||||||||||||||
|
|
|
|
|
|
x + 1 + |
|
|
x − 1 + 2 |
|
|
x |
|
|
|
|
|
|
||||||||||
= |
√ |
|
|
|
|
√ |
|
|
|
−2 √ |
|
|
|
√ |
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
− 1 + x) |
||||||||||||||
|
( x + 1 + x − 1 + 2 x)( x |
|||||||||||||||||||||||||||
– бесконечно малая при x → +∞. Найдем главную часть бесконечно малой β(x) по отношению к основной бесконечно малой α(x). Имеем
|
|
β(x) = −2 |
√ |
|
|
|
|
√ |
|
|
|
1 |
|
|
|
√ |
|
|
|
|
|
|
|
|
= |
|
|
||||||
|
|
|
|
|
|
|
|
√ |
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
( x + 1 + x − 1 + 2 x)( x |
|
− 1 + x) |
|
|
||||||||||||||||||||||
= |
|
−2 |
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
−1 |
= |
−1 |
|
1 |
||||
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
3 |
|
x |
||||||
|
· |
|
x |
|
|
− x |
|
|
− x |
|
|||||||||||||||||||||||
|
|
|
|
|
|
|
4 |
||||||||||||||||||||||||||
|
|
x2 |
( |
1 + 1 |
+ |
1 |
1 + 2)( |
1 |
|
1 |
+ 1) |
4x2 |
|||||||||||||||||||||
|
|
2 |
|||||||||||||||||||||||||||||||
Таким образом, главная часть бесконечно малой β(x) по срав-
нению с основной бесконечно малой x1 (x → +∞) есть величина
|
1 |
1 |
3 |
|
|
2 |
|||
− |
|
|
|
. |
4 |
x |
|||
3
2
.
§12. Элементарные функции
Функции вида
f(x) = a0xm + a1xm−1 + . . . + am−1x + am,
где m ≥ 0 – целое и ai = const, называются целыми рациональными функциями.

§12. Элементарные функции |
89 |
Отношения двух таких многочленов:
f(x) = a0xm + . . . + am b0xn + . . . + bn
называются дробно-рациональными функциями. Совокупность целых рациональных и дробно-рациональных
функций образует класс рациональных функций, т.е. класс функций, получаемых в результате операций сложения, вычитания, умножения, деления и возведения в целую положительную степень, примененных к значениям аргумента x и некоторых постоянных.
Если над аргументом x кроме перечисленных алгебраических операций производится еще извлечение корня конечное число раз и результат не является рациональной функцией (корень не извлекается), то получается иррациональная функция.
ПРИМЕР 1. Функция
5x2 + 4x − 7 f(x) = 3 √
3x2 − 8 x + 4
является иррациональной.
Совокупность всех рациональных и иррациональных функций образует класс явных алгебраических функций. В общем случае алгебраической функцией называется многозначная функция y(x), определяемая неявно посредством уравнения
p0(x)yn + p1(x)yn−1 + . . . + pn−1(x)y + pn(x) = 0,
где n – целое положительное, а коэффициенты p0(x), p1(x),
. . . , pn(x) – целые рациональные функции. Всякая не алгебраическая функция называется трансцендентной функцией. Простейшие (элементарные) трансцендентные функции – это функции вида:
y = ax (a > 0, a = 1), y = loga x (a > 0, a = 1), y = sin x, y = cos x, y = tg x, y = ctg x
и обратные к ним.
Функции алгебраические, элементарные трансцендентные и их конечные комбинации называются элементарными функциями.
Поскольку элементарные функции определяются как результат конечного числа операций над простейшими функциями и сохранение свойства непрерывности при таких действиях установлено, то достаточно проверить непрерывность

90 Глава 3. Непрерывные функции и их свойства
функций
y = xα (α > 0), y = sin x, y = ex.
ПРИМЕР 2. Функция y = ax = exln a есть результат суперпозиции функций y = et и t = x ln a. 

ПРИМЕР 3. Мы имеем y = cos x = ± 1 − sin2 x. 

В качестве примера докажем непрерывность функции y = sin x. Доказательство непрерывности показательной функции и экспоненты можно найти в более объемных учебниках по анализу.
ТЕОРЕМА 12.1. Функция y = sin x непрерывна при всех x R.
Доказательство. Имеем |
|
|
|
|
|||||
sin x |
− |
sin x |
0 |
= 2 sin |
x − x0 |
· |
cos |
x + x0 |
, |
|
|
||||||||
|
|
2 |
2 |
|
|||||
и, так как | sin x| ≤ |x| |
|
x R , то |
|
|
|
|
|||
| sin x − sin x0| ≤ 2 | sin x −2 x0 | ≤ |x − x0|
для любого x. Поэтому, из условия x → x0 следует, что
sin x → sin x0.
