матан

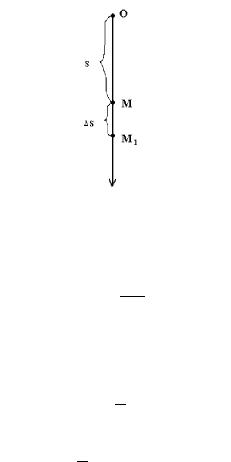
Глава 4

Производная

§1. Понятие производной

Рассмотрим, вначале, некоторые задачи, приводящие к по-

нятию производной.

1.Скорость движения точки

Рассмотрим свободное падение тяжелой материальной точки. Пусть время t отсчитывается от начала падения. Требуется определить скорость ϑ движения точки в данный момент времени t.

Путь, пройденный за время t (когда точка находится в положении M), вычисляется по известной формуле

S = gt2 .

2

Придадим переменной t некоторое приращение ∆t и рассмотрим момент t + ∆t (когда точка будет в положении M1). Для нового значения пути имеем выражение

S + ∆S = g2(t + ∆t)2,

откуда

∆S = g2 2t∆t + ∆t2 .

Разделив ∆S на ∆t, мы получим среднюю скорость падения точки на участке MM1

Мгновенной скоростью ϑ точки в момент времени t называют предел, к которому стремится средняя скорость ϑcp за промежуток ∆t, когда ∆t → 0. В нашем случае

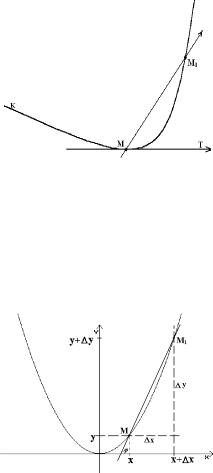
2. Задача о проведении касательной к кривой

Касательной к кривой K в точке M называется предельное положение MT секущей MM1, когда точка M1 вдоль кривой стремится к совпадению с M.

Применим это определение к параболе y = a x2 в точке M = (x, y). Найдем угловой коэффициент tgα касательной в точке М.

Придадим абсциссе x приращение ∆x и перейдем от точки M к точке M1 с абсциссой x + ∆x и ординатой

y + ∆y = a(x + ∆x)2.

Таким образом, угловой коэффициент tgϕ секущей MM1 tgϕ = ∆∆xy = 2ax + a∆x.

Для получения углового коэффициента касательной, нужно перейти здесь к пределу при ∆x → 0. Таким образом,

tgα = lim (2ax + a ∆x) = 2ax.

∆x→0

В общем случае кривой вида y = y(x) угловой коэффици-

Перейдем теперь к определению понятия производной. Пусть y = f(x) – функция, определенная на множестве

E R, и пусть x0 E – точка сгущения E.

ОПРЕДЕЛЕНИЕ 1.1. Говорят, что функция y = f(x) имеет производную по множеству E в точке x0 E, если существует предел при x → x0, x E, разностного отношения

называется производной функции y = f(x) в точке x0 по множеству E и обозначается fE(x0).

Рассмотрим важнейшие частные случаи данного понятия. i) Если E = (a, x0], где a < x0 – произвольная точка, то произ-

водная fE(x0) называется производной слева и обозначается f (x0 − 0).

ii) Если E = [x0, b), где b > x0, то производная fE(x0) называется производной справа и обозначается f (x0 + 0).

iii) Если E = (a, b) и x0 (a, b), то fE(x0) называется производной и обозначается символом f (x0) без указания множества, по которому она берется.

ЗАМЕЧАНИЕ. Из формулы (1) следует, если функция y = f(x) имеет производную в точке x0, то уравнение касательной к ее графику в точке (x0, f(x0)) имеет вид

Y = Y0 + f (x0)(x − x0), Y0 = f(x0).

Нормалью к плоской кривой в точке называется прямая, проходящей через эту точку ортогонально касательной.

УПРАЖНЕНИЕ 1. Написать уравнение нормали к кривой в заданной точке.

Если при x → x0 предел разностного отношения существует и равен ±∞, то эти несобственные числа часто называют бесконечными производными.

Предположим, что функция y = f(x) определена на промежутке a, b . Каждая точка x промежутка является точкой его сгущения. Если в каждой точке x из a, b существует производная f (x), то мы вправе рассматривать f (x) как функцию, определенную на a, b ; эта функция называется производной функцией (или просто производной) от f и обозначается f . Выражения "f дифференцируема на a, b " и "f есть производная от f" означают, что производная функция определена и, значит, f имеет конечную производную в каждой точке < a, b >.

Процесс отыскания производной от данной функции называется дифференцированием.

Функция f (x) (в предположении, что она определена наa, b ) сама может быть дифференцируемой; ее производная (f (x)) обозначается через f (x). При этом f (x) называется первой производной от f, а f (x) – второй производной от f, или производной второго порядка.

Вообще, производные, определяемые таким образом по индукции, обозначаются (если они существуют) символами f(3) (или f ), f(4),. . . , f(n), f(n+1). Функция f(n+1) есть по определению (n + 1)-я производная от f и первая производная

от f(n). Если функция f имеет производные всех порядков n = 1, 2, . . ., то говорят, что f бесконечно дифференцируема.

Часто полагают f(0) = f.

ЗАМЕЧАНИЕ. Приведем список обозначений производной:

Для производных второго порядка и выше используют обозначения: ddx(n)ny , y(n), D(n)y, ... .

§2. Примеры вычисления производных

a) Пусть y = const. Тогда

Отсюда,

(const) = 0.

b) Пусть y = xµ, где µ – произвольное вещественное число. Тогда

В предыдущей главе (см. параграф Асимптотические формулы. Классификация бесконечно малых., формула (1)) показано, что

lim (1 + ε)µ − 1 = µ.

ε→0 ε

Тогда получаем, что

(xµ) = µxµ−1.

c) Пусть y = ax, где a > 0, a = 1. Здесь имеем y = ex ln a и, далее,

Здесь мы использовали соотношение

e∆x ln a − 1 ∆x ln a (∆x → 0) .

Таким образом,

(ax) = ax ln a.

e) Перейдем к тригонометрическим функциям. Рассмотрим сначала y = sin x. Здесь имеем

Тем самым,

(sin x) = cos x.

f) Рассмотрим функцию y = cos x. Как и выше, получаем

(cos x) = − sin x.

УПРАЖНЕНИЕ 1. Докажите самостоятельно указанную выше формулу.

h) Если y = ctgx, то, как в предыдущем случае, имеем

(ctgx) = − 1 . sin2 x

§3. Производная обратной функции

ТЕОРЕМА 3.1. Пусть y = f(x) – функция, определенная на интервале (a, b) и удовлетворяющая там условиям:

1)в точке x0 (a, b) существует f (x0) = 0;

2)существует обратная к f(x) функция x = g(y), непре-

рывная в точке y0 = f(x0).

Тогда обратная функция x = g(y) имеет производную

Доказательство. Придадим значению y0 приращение ∆y. Тогда функция x = g(y) получит приращение ∆x. Заметим, что при ∆y = 0 выполнено ∆x = 0, ибо в противном случае функция y = f(x) не была бы однозначной. Далее имеем

∆x 1 ∆y = ∆y .

∆x

Если теперь положить ∆y → 0, то ∆x → 0 в силу непрерывности x = g(y) в точке y0. Поэтому

Геометрическим истолкованием является следующая формула tgβ = tg1α.

Производная yx есть tg α, где α образован касательной к графику функции y = f(x) с осью Ox. Но обратная функция x = g(y) имеет тот же график, только независимая переменная для нее откладывается по оси Oy. Поэтому производная xy, равна tg β, где β — угол, составленный той же касательной с осью Oy.

Таким образом, выведенная формула сводится к известному соотношению, связывающему тангенсы двух углов α и β, сумма которых равна π2 .

Можно дополнить эту теорему: если f (x0) = 0 или ±∞, то g (y0) = ±∞ или 0, соответственно.

§4. Производные обратных тригонометрических функций

a) Найдем производную функции y = arcsin x, где x (−1, 1), y (−π2 , π2 ). Мы имеем

(Здесь знак + был выбран, поскольку y (−π2 , π2 )).

b) Аналогично, если y = arccos x, (x (−1, 1), y (0, π)), то

c) Пусть y = arctgx и x (−∞, +∞), y (−π2 , π2 ). Находим

x (−∞, +∞), y (0, π). Как и выше, приходим к соотношению

(arcctgx) = −1 +1 x2 .

ЗАМЕЧАНИЕ. Следующие формулы полезно знать на память:

§5. Дифференцируемость и непрерывность

ТЕОРЕМА 5.1. Пусть y = f(x) – функция, определенная на множестве E R, и пусть x0 E – точка сгущения E. Если существует производная fE(x0), то y = f(x) непрерывна в x0.