
матан
.pdf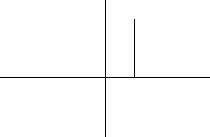
§5. Первый "замечательный" предел |
61 |
y
C
B
x
0 A x
Пусть угол BOA = x. Площадь сектора ОВА равна x2 . Площадь OBA равна 12 sin x. Площадь OCA равна 12 tg x. Так как
то |
пл. OBA < пл. сектора OBA < пл. OCA, |
|
|
|
|||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
1 |
|
|
|
|
|
|
x |
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
sin x < |
< |
tg x, |
|
|
|
|
|
|
|
||||||||||||||||||||||||
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||
|
|
|
|
|
2 |
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
что и требовалось для доказательства (1). |
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||
|
Покажем, что x (0, π4 ) выполнено |
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
sin x |
|
|
|
|
x2 |
|
|
|
|
|
|
|
|
(2) |
||||||||||||
|
|
|
|
|
|
|
0 < 1 − |
|
|
|
|
< √ |
|
|
. |
|
|
|
|
|
|
|
|
||||||||||||||||||
|
|
|
|
|
x |
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||
Действительно, из (1) следует, что |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||
|
|
|
|
|
sin x |
< 1 < |
tg x |
= |
sin x |
|
|
|
1 |
|
|
. |
|
|
|
|
|
|
|
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||
|
|
|
|
|
|
x |
|
|
|
|
x |
|
|
|
|
x cos x |
|
|
|
|
|
|
|
||||||||||||||||||
Отсюда, |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
sin x |
1 |
|
|
|
|
|
|
|
|
|
sin x |
1 |
|
|
|
|
|
|
|
|||||||||||||||||
|
|
|
0 < 1 − |
|
|
< ( |
|
− 1) |
|
|
|
< |
|
|
− 1. |
|
|
|
|||||||||||||||||||||||
|
|
|
x |
cos x |
|
x |
cos x |
|
|
|
|||||||||||||||||||||||||||||||
Однако, при x (0, π4 ) имеем |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||
|
1 |
|
1 = |
1 − cos x |
= 2 sin2 x2 < |
2(x2 )2 |
< |
|
|
|
x2 |
= |
x2 , |
||||||||||||||||||||||||||||
|
cos x |
− |
|
cos x |
|
|
cos x |
|
|
|
|
cos x |
|
|
2(cos( |
π )) |
|
√ |
|
|
|||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
4 |
|
2 |
||
что и доказывает (2). |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
Покажем, что x (−π4 , π4 ), |
x = 0 выполнено |
|
|
|
||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
sin x |
|
|
|
|
x2 |
|
|
|
|
|
|
|
|
(3) |
||||||||||||
|
|
|
|
|
|
|
0 < 1 − |
|
< √ |
|
. |
|
|
|
|
|
|
|
|
||||||||||||||||||||||
|
|
|
|
|
|
|
x |
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||

62 |
Глава 2. Предел функции |
Действительно, пусть x < 0. Положим y = −x. Тогда y > 0
иx (−π4 , 0) имеем
1 − sin x = 1 − sin(−y) = 1 − sin y. x (−y) y
Учитывая данное равенство, неравенство (3) непосредственно следует из (2).
Докажем существование предела. Пусть ε > 0 – произволь-
но. Выберем |
√4 |
|
|
π |
|
|
2 |
|
}. |
||
|
δ(ε) = min{ |
2ε |
, |
|
|
|
4 |
Тогда x = 0 : |x| < δ(ε) заключаем, что |x| < π4 и, значит,
справедливо неравенство (3). Тогда, пользуясь (3), находим, что
1 − |
x |
|
< √2 < √2 ≤ √2 |
|
|
= ε. |
|||||||||||||||
|
|
|
|
|
|
2 |
|
|
2 |
|
|
√4 |
|
|
|
|
2 |
|
|||
|
sin x |
|
|
x |
|
|
δ |
|
|
( |
|
|
2ε |
) |
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
Последнее неравенство |
доказывает теорему. |
|
|
||||||||||||||||||
ПРИМЕР 1. Мы имеем |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
lim |
tg x |
= lim |
|
|
sin x |
|
= 1. |
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
x→0 |
x |
|
|
x→0 x cos x |
|
|
|
|
|
|
||||||||||
§6. Простейшие свойства предела функции. Односторонние пределы
ТЕОРЕМА 6.1. Предположим, что заданные на одном и том же множестве функции f(x) и g(x) имеют при x → a пределами A и B соответcтвенно. Тогда
1) функции f(x)±g(x), f(x)·g(x) имеют при x → a пределы, причем
lim(f(x) ± g(x)) = A ± B,
x→a
lim(f(x) · g(x)) = AB;
x→a
2) если B = 0, то функция |
f(x) |
|
имеет предел при |
||||
g(x) |
|||||||
x → a, причем |
|
|
|
|
|
|
|
lim |
f(x) |
= |
|
A |
. |
||
|
|
||||||
x→a g(x) |
|
|
B |
||||

§6. Простейшие свойства предела функции |
63 |
Доказательство. Пусть {xn} → a, (xn = a, n = 1, 2, . . .) –
произвольная последовательность точек из области определения функций f(x) и g(x). Последовательности {f(xn)} и {g(xn)} имеют пределы A и B. Пользуясь соответствующим утверждением для последовательностей, заключаем о существовании пределов последовательностей
{f(xn) ± g(xn)}, {f(xn) · g(xn)}, { |
f(xn) |
} |
|
|
||||
g(xn) |
|
|
||||||
и справедливости равенств |
|
|
|
|
|
|
|
|
nlim (f(xn) ± g(xn)) = A ± B, |
nlim |
f(xn) |
|
A |
|
|||
|
|
= |
|
, |
||||
g(x |
) |
B |
||||||
→∞ |
→∞ |
|
n |
|
|
|
|
|
lim f(xn) · g(xn) = AB.
n→∞
В силу произвола в выборе последовательности {xn}, из теоремы 4.1, получаем требуемое.
ТЕОРЕМА 6.2. Пусть y = f(x) и y = g(x) – функции с общей областью определения X R, и a – точка сгуще-
ния X. Пусть также существуют пределы lim f(x) = A
x→a
и lim g(x) = B. Тогда, если
x→a
f(x) ≤ g(x) x X,
то A ≤ B.
Доказательство. Пусть {xn} → a (xn = a, n = 1, 2, . . .) –
произвольная последовательность. Тогда f(xn) ≤ g(xn) n = 1, 2, . . . . Пользуясь теоремой о предельном переходе в неравенстве для последовательностей, заключаем, что A ≤ B. 
УПРАЖНЕНИЕ 1. Покажите, что в условиях теоремы достаточно выполнения неравенства f(x) ≤ g(x) в некоторой окрестности точки a.

64 |
Глава 2. Предел функции |
ТЕОРЕМА 6.3. Пусть y = f(x), y = g(x), y = h(x)
функции с общей областью определения X R и a – точка сгущения X. Предположим, что
x a |
и |
x a |
lim f(x) = A |
|
lim g(x) = A. |
→ |
|
→ |
Тогда, если
f(x) ≤ h(x) ≤ g(x) x X,
то существует lim h(x) = A.
x→a
Докажите самостоятельно.
ОПРЕДЕЛЕНИЕ 6.1. Говорят, что функция y = f(x) имеет пределом число A при x → a справа (слева), если для любой последовательности точек {xn} → a, xn > a (xn < a) выполнено f(xn) → A. Обозначения:
lim f(x) = A и |
lim f(x) = A. |
x→a+0 |
x→a−0 |
В случае a = 0 используем специальные обозначения
lim f(x) = A и |
lim f(x) = A. |
x→+0 |
x→−0 |
ОПРЕДЕЛЕНИЕ 6.2. Говорят, что функция y = f(x) имеет пределом число A при x → a справа (слева), если
ε > 0 δ(ε) > 0 : x > a (x < a), |x − a| < δ(ε)
выполнено |f(x) − A| < ε.
ЗАМЕЧАНИЕ. Иногда lim f(x) обозначают символом
x→a+0
f(a + 0), а lim f(x), соответственно, символом f(a − 0).
x→a−0
ТЕОРЕМА 6.4. Определения 6.1 и 6.2 предела функции в точке справа и слева эквивалентны.
Доказательство. Рассуждения почти дословно повторяют доказательство теоремы об эквивалентности для двустороннего предела. 
ТЕОРЕМА 6.5. Двусторонний предел функции при x → a существует тогда и только тогда, когда существуют порознь и равны между собой односторонние пределы данной функции в указанной точке.

§7. Монотонные функции |
65 |
Доказательство. Ясно, что если существует двусторонний предел, то существуют порознь и равны между собой односторонние пределы.
Обратно, предположим, что существуют lim f(x) = A.
x→a±0
Зададим ε > 0. Тогда существуют δ1(ε), δ2(ε) > 0 такие, что
x > a, |x − a| < δ1(ε) выполнено |f(x) − A| < ε. |
(1) |
и |
|
x < a, |x − a| < δ2(ε) выполнено |f(x) − A| < ε. |
(2) |
Положим δ(ε) = min{δ1(ε), δ2(ε)}. При |x − a| < δ(ε) неравенства (1) и (2) выполняются одновременно, а потому существует
lim f(x) = A.
x→a
УПРАЖНЕНИЕ 2. Сформулировать и доказать теоремы о единственности предела функции в точке и о единственности односторонних пределов функции в точке.
§7. Монотонные функции
ОПРЕДЕЛЕНИЕ 7.1. Функция y = f(x) называется
i) монотонно |
возрастающей, |
если |
x1 |
< |
x2 |
выполнено |
f(x1) < f(x2), |
|
|
|
|
|
|
ii) монотонно |
убывающей, |
если |
x1 |
< |
x2 |
выполнено |
f(x1) > f(x2), |
|
|
|
|
|
|
iii)невозрастающей, если x1 < x2 выполнено f(x1) ≥ f(x2),
iv)неубывающей, если x1 < x2 выполнено f(x1) ≤ f(x2).
Функции перечисленных классов называются монотонными.
ТЕОРЕМА 7.1. Если y = f(x) монотонна на интервале (a, b), то в каждой точке x0 (a, b) существуют односторонние пределы справа и слева.
Доказательство. Предположим, что f(x) неубывает на интервале (a, b). Фиксируем x0 (a, b). Тогда для всех x (a, x0) выполнено
f(x) ≤ f(x0). |
(1) |

66 |
Глава 2. Предел функции |
Пусть Y – область значений сужения f(x) на интервале (a, x0). В силу соотношения (1) множество Y ограничено сверху числом f(x0). Обозначим
c = sup Y = sup f(x).
x (a,x0)
Покажем, что c = lim f(x). Зададим произвольно ε > 0.
x→x0−0
По определению точной верхней грани функции, найдется точка x (a, x0) такая, что
y = f(x ) > c − ε.
Положим δ(ε) = x0 − x . Тогда x (x0 − δ(ε), x0), выполнено x < x < x0 и потому
f(x ) ≤ f(x) ≤ c.
Тем самым,
0 ≤ c − f(x) ≤ c − f(x ) < c − (c − ε) = ε,
т.е. c = lim f(x). Аналогичным образом устанавливается
x→x0−0
существование предела справа.
ЗАМЕЧАНИЕ. В процессе доказательства теоремы мы доказали также следующее утверждение: если y = f(x) неубывает (невозрастает) на интервале (a, x0) и ограничена сверху
(снизу), то она имеет предел lim f(x).
x→x0−0
§8. Второй "замечательный" предел
ТЕОРЕМА 8.1. Справедливо равенство
1
lim(1 + x)x = e.
x→0
Доказательство. Покажем, что
1
lim (1 + x)x = e.
x→+0
Будем использовать определение предела справа в смысле Гейне. Пусть xn > 0, xn → 0 при n → ∞ – произвольная последовательность. Выберем целые числа Kn так, чтобы
1
Kn ≤ xn < Kn + 1.
§8. Второй "замечательный" предел |
67 |
Это можно сделать, положив, например, Kn = [1/xn]. Тогда имеем
|
1 |
|
|
1 |
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|||||||||
|
|
< xn ≤ |
|
|
|
1 + |
|
|
|
|
|
< 1 + xn ≤ |
1 + |
|
|
|
|||||||||||||||
Kn + 1 |
Kn |
Kn + 1 |
Kn |
||||||||||||||||||||||||||||
(1 + |
1 |
|
|
|
|
Kn |
|
|
|
1 |
|
1 |
|
|
Kn+1 |
|
|
||||||||||||||
|
|
|
|
|
|
|
|||||||||||||||||||||||||
|
Kn + 1 |
) |
|
< (1 + xn)xn < (1 + |
Kn |
) |
|
|
|
||||||||||||||||||||||
|
(1 + |
|
1 |
)Kn+1 |
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
1 |
|
|
||||||||
|
Kn+1 |
|
|
1 |
|
|
|
|
|
Kn |
|
|
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
1 + |
|
1 |
|
|
|
|
< (1 + xn)xn < (1 + |
Kn |
) |
|
|
(1 + |
Kn |
). |
|||||||||||||||||
Kn+1 |
|
|
|
|
|
||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
Поскольку (1 + n1 )n → e и Kn → ∞ при n → ∞, то левая и правая части двойного неравенства также стремятся к e. Пользуясь принципом "сжатой" последовательности, заключаем, что
1
lim (1 + xn)xn = e.
n→∞
Покажем, что
1
lim (1 + x)x = e.
x→−0
Положим y = −x. Тогда
1 |
1 |
= |
(1 + x)x = (1 |
− y)−y |
1 |
1 |
= ( |
1 − y + y)y |
= |
||
|
|
|
|
|
1 |
|
(1 − y)y |
|
|
1 − y |
|
||
y
= 1 + 1 − y
1 y
1−y
|
|
y |
y |
y |
1 |
|
|
|
|
|
|
|
|
||
= 1 + |
|
|
(1+ |
|
|
) = (1+t) t |
(1+t), |
|
− y |
|
− y |
||||
1 |
1 |
|
|
||||
где t = 1−y y . При x → −0 имеем: y → +0, и, стало быть, t → +0. Отсюда следует, что
lim |
1 |
1 |
(1 + t) = e. |
(1 + x)x = lim (1 + t) t |
|||
x→−0 |
|
t→+0 |
|
Наконец пользуясь теоремой о связи двустороннего предела с односторонним, заключаем о справедливости равенства
1
lim(1 + x)x = e.
x→0

68 |
Глава 2. Предел функции |
§9. Критерий Коши существования предела функции
ТЕОРЕМА 9.1. Для того, чтобы функция y = f(x) имела предел при x → x0 необходимо и достаточно, чтобы
ε > 0 δ(ε) > 0 : x = x0, x = x0,
|x − x0| < δ(ε), |x − x0| < δ(ε)
выполнялось
|f(x ) − f(x )| < ε.
Доказательство. Необходимость. Предположим, что
lim f(x) = A. Покажем, что функция удовлетворяет усло-
x→x0
вию критерия Коши. Зададим произвольно ε > 0. Т.к. f(x) → A, при x → x0, то
δ(ε) : x = x0, |x − x0| < δ(ε) |
выполнено |
|
|f(x) − A| < |
ε |
||||||||||
|
|
. |
||||||||||||
|
2 |
|||||||||||||
Поэтому |
x , x = x |
, x |
− |
x |
0| |
< δ(ε), |
| |
x |
− |
x |
0| |
< δ(ε) |
||
0 |
| |
|
|
|
|
|
|
|
||||||
получаем
|f(x ) − f(x )| = |f(x ) − A + A − f(x )| ≤
≤ |f(x ) − A| + |f(x ) − A| < 2ε + 2ε = ε.
Достаточность. Пусть y = f(x) удовлетворяет в окрестно-
сти x0 условию Коши. Покажем, что lim f(x). Восполь-
x→x0
зуемся определением предела функции в точке "на языке" последовательностей (т.е. в смысле Гейне). Пусть {xn} – произвольная последовательность такая, что xn = x0, xn → x0
при n → ∞. Требуется доказать, что существует lim f(xn).
n→∞
Зададим ε > 0. Найдем δ(ε), участвующее в формулировке критерия Коши. Так как xn → x0 , то по определению предела последовательности
N(δ(ε)) : n > N(δ(ε)) выполнено |xn − x0| < δ(ε)
(воспользовались ). Поэтому
|f(xn) − f(xm)| < ε n, m > N(δ(ε)).
Таким образом, последовательность {f(xn)} является фундаментальной. Согласно критерию Коши для последовательностей она имеет предел.
§9. Критерий Коши существования предела функции |
69 |
Покажем, что этот предел не зависит от выбора последовательности {xn}. Предположим противное, т.е. найдутся последовательности {xn} и {xn} такие, что
xn = x0, xn = x0, lim xn = lim xn = x0
n→∞ n→∞
и
nlim f(xn) = nlim f(xn). |
||
→∞ |
→∞ |
|
Тогда, полагая |
|
|
xn, если |
n |
четное, |
xn = xn, если |
n −− |
нечетное, |
заключаем, что последовательность {f(xn )} предела не имеет. Получаем противоречие. 
Глава 3
Непрерывные функции и их свойства
§1. Непрерывность и разрывы функции
Пусть y = f(x) – функция, определ¨енная на множестве E R, и пусть x0 E – точка сгущения множества E.
ОПРЕДЕЛЕНИЕ 1.1. Говорят, что y = f(x) непрерывна в точке x0, если
lim f(x) = f(x0).
x→x0
Если предела функции в точке не существует или предел существует, но не равен значению функции в этой точке, то такая точка называется точкой разрыва функции.
Если точка x0 не является точкой сгущения (т.е. является изолированной точкой области определения), то о пределе в этой точке (а, следовательно, о непрерывности или разрывах функции) говорить нельзя.
ЗАМЕЧАНИЕ. Иногда вопрос о пределе функции в изолированной точке множества ее определения решается несколько иначе. А именно, считают по определению, что предел всегда существует и равен f(x0). Соответственно, функция в изолированной точке области определения всегда непрерывна.
Если обозначить через ∆x = x−x0 приращение аргумента, а через ∆f = f(x) − f(x0) – приращение функции, то f(x)
непрерывна в x0 тогда и только тогда, когда lim ∆f = 0.
∆x→0
ОПРЕДЕЛЕНИЕ 1.2. Говорят, что y = f(x) непрерывна в точке x0 справа (слева), если
lim |
f(x) = f(x0) ( lim f(x) = f(x0)). |
x→x0+0 |
x→x0−0 |
