матан

В каком месте доказательства использовано определение мел-

кости разбиения P как максимума диаметров дуг pipi+1? Подсказка: рассмотреть замкнутые кривые.

ОПРЕДЕЛЕНИЕ 1.1. Если существует предел

→

не зависящий от способа вписывания ломаной p0p1 . . . pn, то его величина называется длиной дуги γ, а сама дуга γ — спрямляемой. Здесь length p0p1 . . . pn — длина ломаной p0p1 . . . pn.

1.3.Вычисление длины дуги в декартовых координатах

ТЕОРЕМА 1.1. Если r = r(t) = (ϕ(t), ψ(t)) – непрерыв-

n−1

=(ϕ(ti+1) − ϕ(ti))2 + (ψ(ti+1) − ψ(ti))2.

i=0

По формуле конечных приращений Лагранжа находим

|pipi+1| = (ϕ(ti+1) − ϕ(ti))2 + (ψ(ti+1) − ψ(ti))2 =

1.4.Длина непараметрической дуги

ТЕОРЕМА 1.2. Если дуга γ является графиком непрерывно дифференцируемой функции f, заданной на [a, b], то

Доказательство. Перепишем γ в параметрическом виде. Положим x = t. Тогда y = f(t) и t [a, b]. По доказанному выше имеем

1.5.Длина дуги в полярных координатах

Напомним, что полярные координаты

(r, ϕ), r ≥ 0, 0 ≤ ϕ < 2π,

точки A на плоскости суть расстояние r до A от некоторой выделенной точки O и угол ϕ, отсчитываемый в положительном направлении3 от некоторого выделенного направления,

например положительного направления оси Ox, до вектора

−→

OA.

Если точка A имеет полярные координаты (r, ϕ), то ее декартовы прямоугольные координаты (x, y) находятся по формулам

x = r cos ϕ, y = r sin ϕ.

ТЕОРЕМА 1.3. Если дуга (или кривая) γ задана в полярных координатах (r, ϕ) посредством уравнения r = r(ϕ), где r(ϕ) – непрерывно дифференцируемая на [α, β] функция, то

β

length γ = r 2(ϕ) + r2(ϕ) dϕ.

α

3т.е. против часовой стрелки

Доказательство. Легко видеть, что в декартовых координатах γ может быть записана в виде

x = r(ϕ) cos ϕ, y = r(ϕ) sin ϕ.

Поэтому мы имеем

x 2(ϕ) + y 2(ϕ) =

= (r cos ϕ − r sin ϕ)2 + (r sin ϕ + r cos ϕ)2 =

=r 2(ϕ) + r2(ϕ)

и, пользуясь формулой для длины дуги в декартовых координатах, получаем

ТЕОРЕМА 1.4. Если дуга (или кривая) γ задана в полярных координатах (r, ϕ) посредством уравнения ϕ = ϕ(r), где 0 < r1 < r < r2 < ∞ – непрерывно дифференцируемая на [r1, r2] функция, то

r2

r1

Доказательство. Переходя к декартовым координатам, имеем

x = r cos ϕ(r), y = r sin ϕ(r), r1 < r < r2.

=(cos ϕ − r sin ϕ ϕ )2 + (sin ϕ + r cos ϕ ϕ )2 =

=1 + r2ϕ 2.

Как и выше, приходим к нужной формуле.

ПРИМЕР 1. Найдем длину куска γ спирали, описываемой уравнением ϕ = r, где 0 ≤ r ≤ R < ∞.

Мы имеем

R

0

Используя формулу интегрирования по частям, несложно получить (проверьте!)

§2. Площадь криволинейной трапеции

Площадь плоской фигуры, являющейся многоугольником, считаем известной. Введем понятие площади плоской фигуры Q, т.е. части плоскости, ограниченной простой замкнутой кривой L.

Пусть {S(M)} – множество площадей многоугольников M, содержащихся в Q, а {S(M)} – множество площадей многоугольников, содержащих Q. Множество {S(M)} ограничено

сверху, а {S(M)} – снизу.

Мы определяем нижнюю площадь фигуры

A(Q) = sup{S(M)}

M

и верхнюю площадь —

A(Q) = inf{S(M)}.

M

ОПРЕДЕЛЕНИЕ 2.1. Плоская фигура Q называется квадрируемой, если верхняя площадь A(Q) этой фигуры совпадает с нижней площадью A(Q). При этом число

A = A(Q) = A(Q) называется площадью фигуры Q.

ТЕОРЕМА 2.1. Для того, чтобы плоская фигура Q была квадрируемой, необходимо и достаточно, чтобы для произвольного ε > 0 нашлись многоугольники M1 Q и M2 Q такие, что S(M2) − S(M1) < ε.

Доказательство. Доказательство проведите самостоятельно. Необходимость сразу следует из определения точных верхней и нижней граней. Достаточность очевидна (см., также, доказательство критерия интегрируемости по Риману).

ТЕОРЕМА 2.2. Если граница L ограниченной плоской фигуры Q представляет собой замкнутую спрямляемую кривую, то Q квадрируема.

Доказательство. Утверждение понятно с геометрической точки зрения. Именно, если L спрямляема, то найдутся многоугольники M (возможно с самопересечениями), границы которых будут сколь угодно тесно примыкать к кривой L. Отсюда вытекает, что будут существовать многоугольники M1 Q и M2 Q с близкими по величине площадями. Этого, очевидно, достаточно для квадрируемости Q.

Вместе с тем, рассуждения, обосновывающие с достаточной степенью строгости эти соображения, довольно громоздки (см., например, Г.М. Фихтенгольц, Курс дифференциального и интегрального исчисления, т. II, п. 337).

УПРАЖНЕНИЕ 1. Разобрать доказательство самостоятельно.

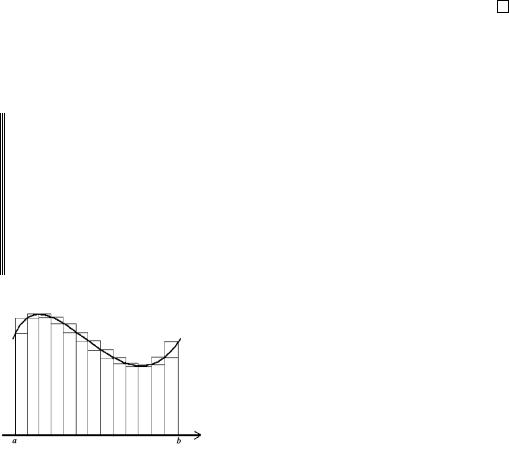
ОПРЕДЕЛЕНИЕ 2.2. Криволинейной трапецией называется плоская фигура, ограниченная графиком заданной на [a, b], непрерывной и неотрицательной функции y = f(x), прямыми x = a и x = b, и осью Ox.

ТЕОРЕМА 2.3. Криволинейная трапеция Q представляет собой квадрируемую фигуру, площадь которой вычисляется по формуле

b

|Q| = A(Q) = f(x) dx.

a

Доказательство. Здесь f непрерывна и, тем самым, интегрируема. Поэтому согласно критерию интегрируемости для произвольного ε > 0 найдется разбиение T отрезка [a, b] такое, что

S(T ) − s(T ) < ε.

Заметим, что S(T ) и s(T ) суть площади ступенчатых фигур, являющихся также и многоугольниками. Пользуясь критерием квадрируемости плоской фигуры, получаем нужное.

Формула для вычисления площади криволинейной трапеции получается предельным переходом при ε → 0.

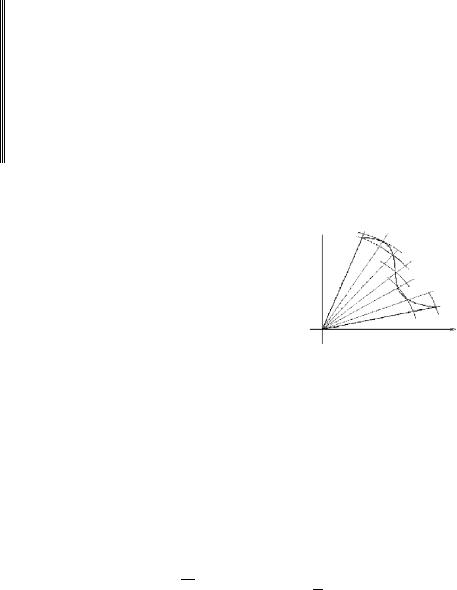
§3. Площадь криволинейного сектора

Предположим, что дуга L задана в полярной системе координат посредством непрерывной функции r = r(θ), где

Пусть E – ограниченная фигура в трехмерном евклидовом пространстве R3 с границей, являющейся замкнутой поверхностью без самопересечений.

Пусть {V (M1)} – множество объемов многогранников M1 E, {V (M2)} — множество объемов многогранников M2 E. Множество {V (M1)} ограничено сверху, а множе-

ство {V (M2)} – снизу.

Пусть V (E) = supM1 V (M1) – нижний объем и V (E) = infM2 V (M2) – верхний объем фигуры E. Ясно, что

V (E) ≤ V (E).

ОПРЕДЕЛЕНИЕ 4.1. Фигура E называется кубируемой,

если V (E) = V (E). Величина V (E) = V = V называется в этом случае объемом фигуры.

ТЕОРЕМА 4.1. Для того, чтобы тело E R3 было кубируемым, необходимо и достаточно, чтобы ε > 0 существовали многогранники M1 E и M2 E такие, что V (M2) − V (M1) < ε.

Доказательство провести самостоятельно (см. комментарии к доказательству соответствующей теоремы для квадрируемых фигур на плоскости).

ПРИМЕР 1. Пусть E – прямой цилиндр с основанием Q, где Q – квадрируемая фигура площади S, h – высота цилиндра. Тогда V (E) = S h.

В самом деле, если Q квадрируема, то существуют многоугольники M1 Q и M2 Q, для которых

ε

S(M2) − S(M1) < h.

Построим прямые призмы M1 и M2 высоты h и основани-